§2.2热力学第二定律的经典表述 Kelvin&Plank总结这一教训来表述热力学第二定律: “不可能造成这样一种机器,这种机器能够循环不断地工作,它仅仅 从单一热源吸热变为功而没有任何其它变化。”第二类永动机。 热力学第二定律的经典叙述可简化为: ”第二类永动机是不可能造成的。” Clausius的表述为: “不可能把热从低温物体传到高温物体而不引起其它变化。” 第二类 永动机 W 源 W 高温热 22 热机 低温热源 T 6
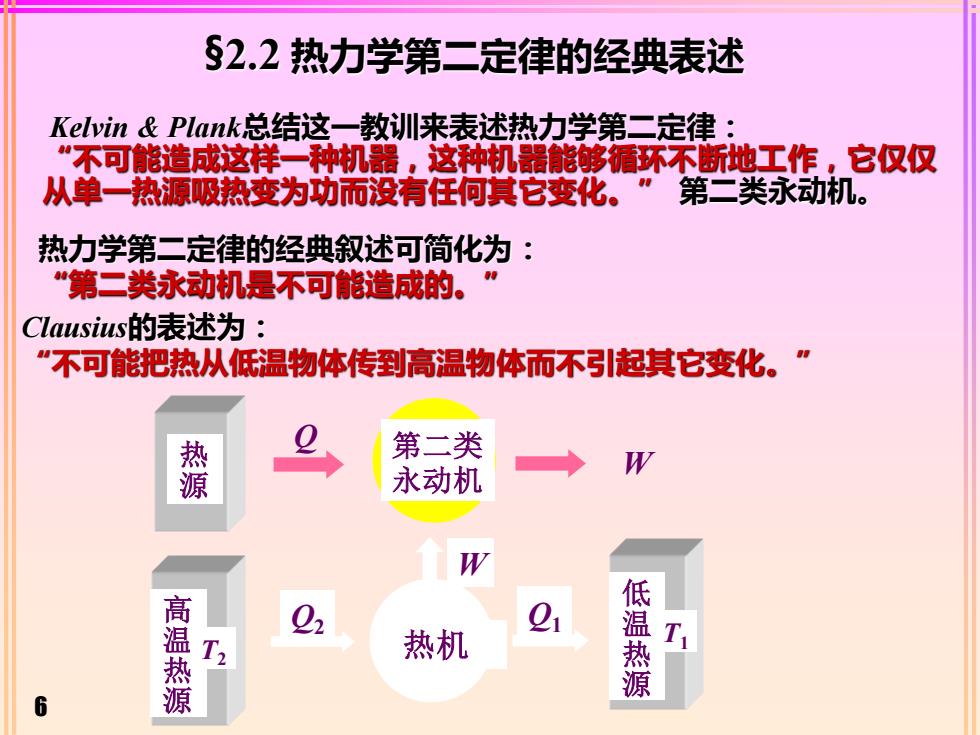
6 Kelvin & Plank总结这一教训来表述热力学第二定律: “不可能造成这样一种机器,这种机器能够循环不断地工作,它仅仅 从单一热源吸热变为功而没有任何其它变化。” 第二类永动机。 热力学第二定律的经典叙述可简化为: “第二类永动机是不可能造成的。” Clausius的表述为: “不可能把热从低温物体传到高温物体而不引起其它变化。” §2.2 热力学第二定律的经典表述 热 源 第二类 永动机 Q W 高 温 热 源 热机 Q2 T2 W 低 温 热 源 T1 Q1
§2.3卡诺循环和卡诺定理 Carnot Cycle and Carnot Theorem n(热机效率)=-W/02 卡诺热机:理想热机 =1+0/02 卡诺热机工作介质为理想气体,在T,T2 两热源之间工作,经过一个由四个可逆过 (W<0,2<0) 程组成的循环过程—卡诺循环。 高温热源2 12 B(P2,V2) 吸热22 D下 热机一→做出功W PAVA TiCO0,囹 放热21 A→B:定温可逆膨涨, 吸热Q2; B-→C:绝热可逆膨胀; C→D:定温可逆压缩,放热21; 低温热源 D→A:绝热可逆压缩;
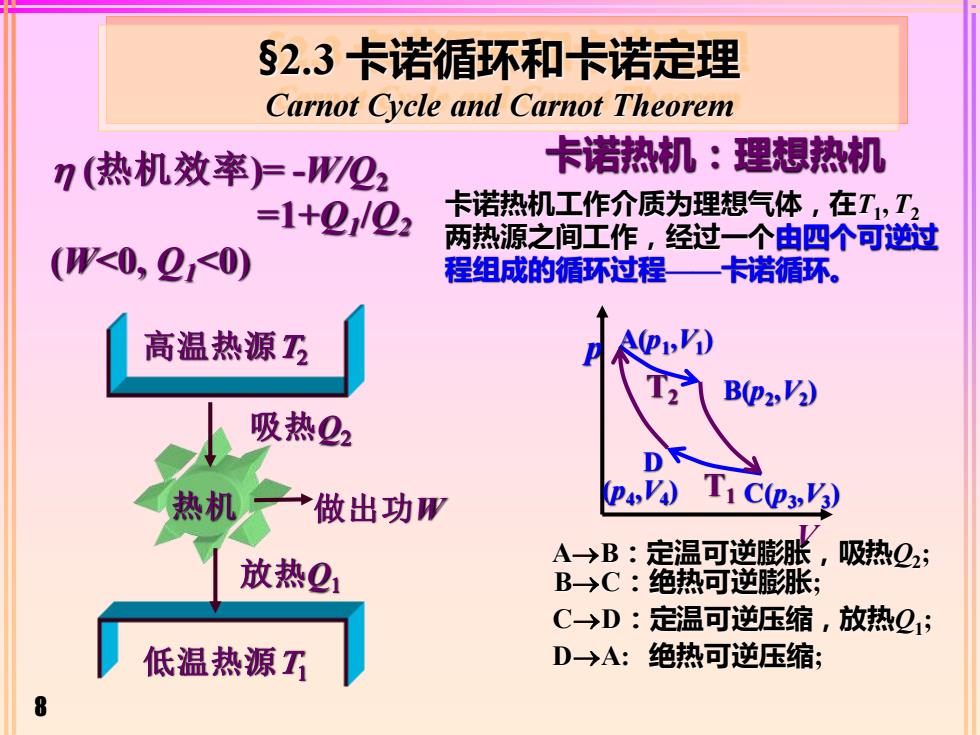
8 §2.3 卡诺循环和卡诺定理 Carnot Cycle and Carnot Theorem (热机效率)= -W/Q2 =1+Q1 /Q2 (W<0, Q1<0) 低温热源T1 高温热源T2 吸热Q2 放热Q1 做出功W 卡诺热机:理想热机 卡诺热机工作介质为理想气体,在T1 , T2 两热源之间工作,经过一个由四个可逆过 程组成的循环过程——卡诺循环。 p V A(p1 ,V1 ) B(p2 ,V2 ) T1 C(p3 ,V3 ) D (p4 ,V4 ) T2 B→C:绝热可逆膨胀; D→A: 绝热可逆压缩; A→B:定温可逆膨胀,吸热Q2 ; C→D:定温可逆压缩,放热Q1 ;
1.Carnot循环 工作物质:1mol理想气体 在印~V图上可以分为四步: 过程1:等温可逆膨胀A(P,Y,I)→B(P2,2,T) △U1=0 W.=-nRT, A,T2) B(p,V,T) Q2=-W T 系统所作功如AB曲 线下的面积所示。 a b 9
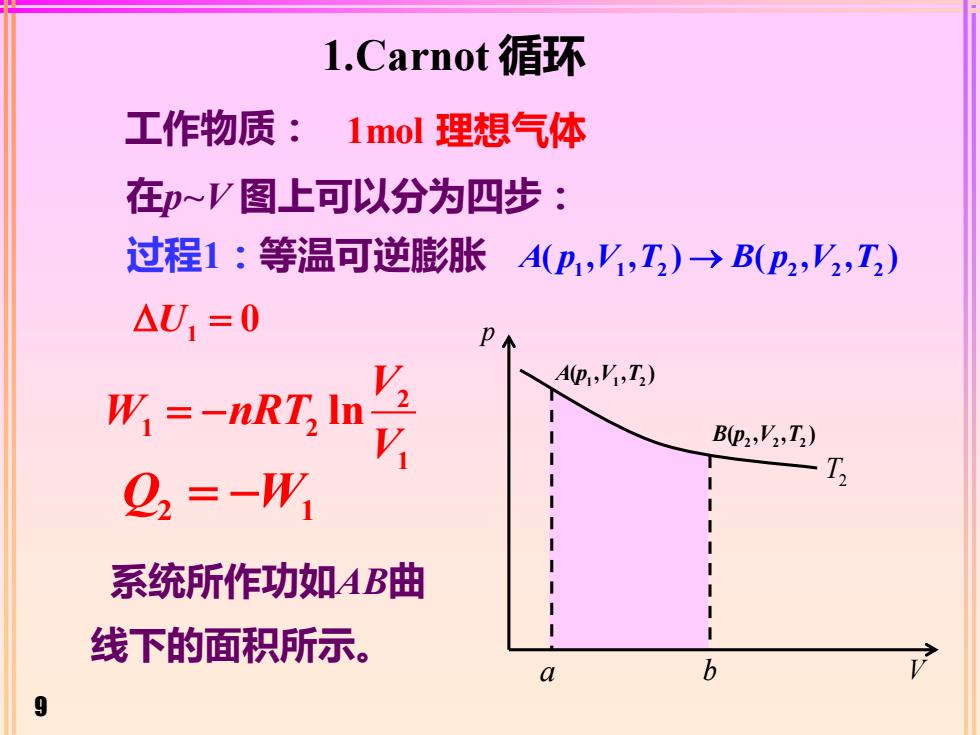
9 工作物质: 过程1:等温可逆膨胀 1 1 2 2 2 2 A p V T B p V T ( , , ) ( , , ) → 1 = U 0 2 1 2 1 lnV W nRT V = − 系统所作功如AB曲 线下的面积所示。 Q W 2 1 = − 1.Carnot 循环 在p~V 图上可以分为四步: 1mol 理想气体 p 1 1 2 A p V T ( , , ) 2 2 2 B p V T ( , , ) V T2 a b
过程2:绝热可逆膨胀 B(p2,V,T2)→Cp3,V,T) 2 =0 W,=△U, Ap1,',T2) Bp2,V2,T2) T C3,T) 系统所作功如BC曲 线下的面积所示。 a b 10
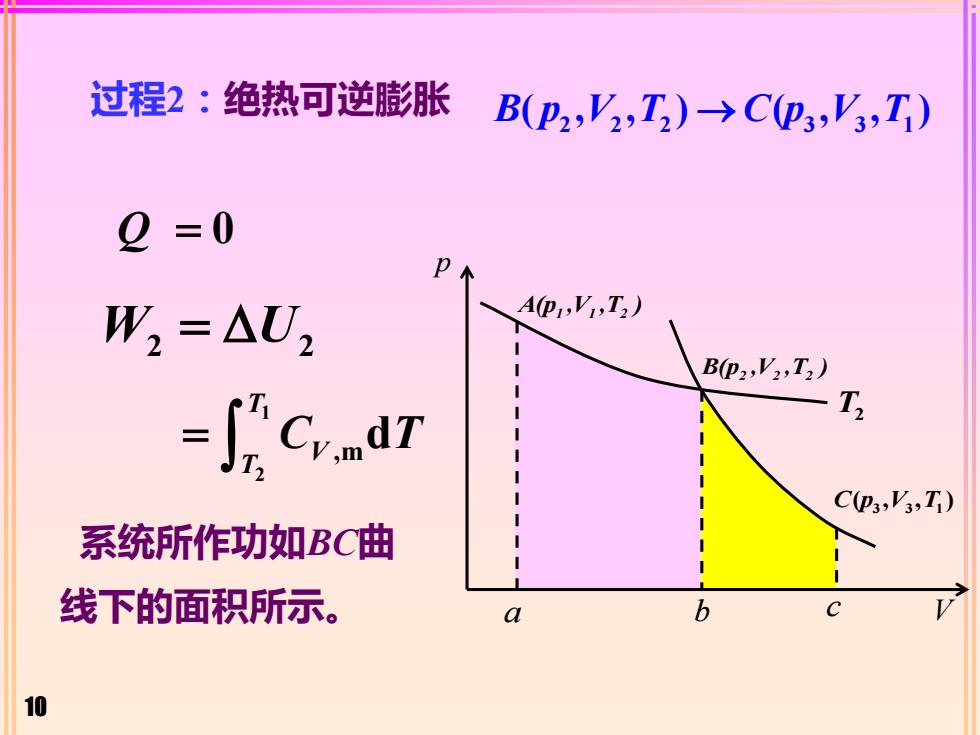
10 过程2:绝热可逆膨胀 2 2 2 3 3 1 B p V T C p V T ( , , ) ( , , ) → Q = 0 W U 2 2 = 系统所作功如BC曲 线下的面积所示。 1 2 ,md T V T = C T p A(p ,V ,T ) 1 1 2 B(p ,V ,T ) 2 2 2 3 3 1 C p V T ( , , )V T2 a b c

过程3:等温可逆压缩 C(P3,V,T)→Dp4,V4,T) △U3=0 A(PV,T) W3=-nRT In Bp2,'3,T2) T 2=-W3 D(PVT) C0,',T) 环境对系统所作功如 DC曲线下的面积所示 a d b C 11
11 3 = U 0 环境对系统所作功如 DC曲线下的面积所示 Q W 1 3 = − 4 3 1 3 lnV W nRT V = − 过程3:等温可逆压缩 3 3 1 4 4 1 C p V T D p V T ( , , ) ( , , ) → p 1 1 2 A p V T ( , , ) 2 2 2 B p V T ( , , ) 3 3 1 C p V T ( , , ) 4 4 1 D p V T ( , , ) V T2 T1 a d b c