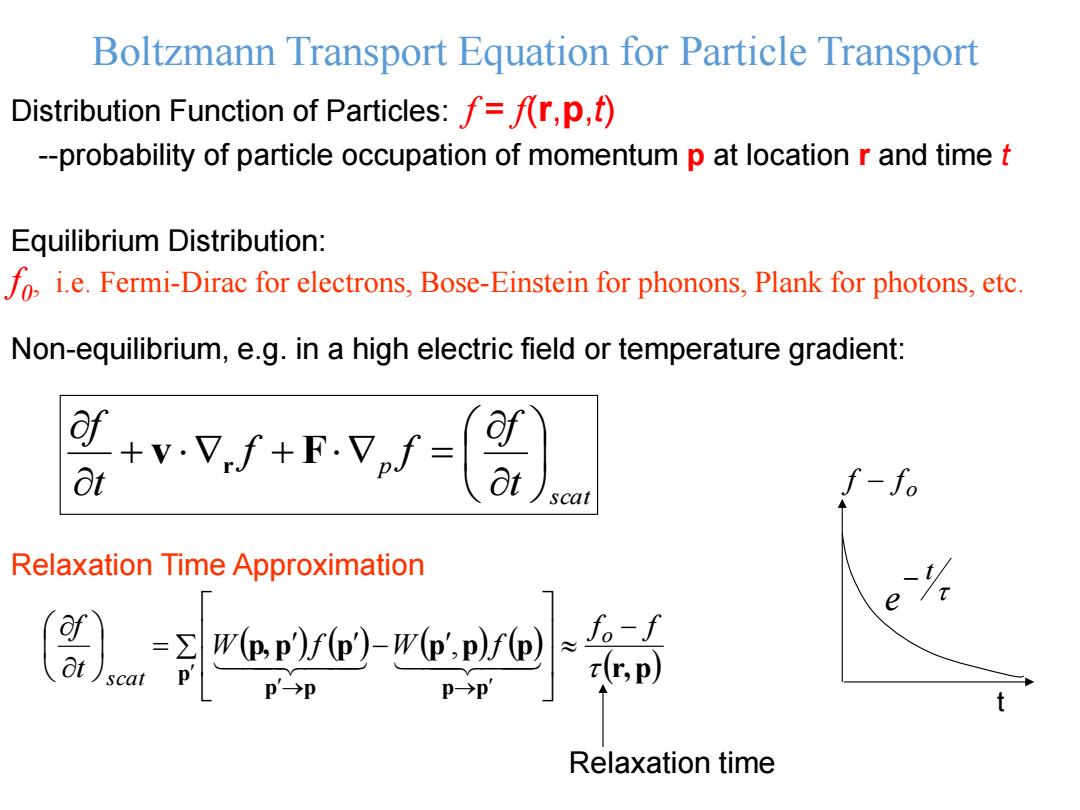
Boltzmann Transport Equation for Particle Transport Distribution Function of Particles:f=f(r,p,) --probability of particle occupation of momentum p at location r and time t Equilibrium Distribution: o i.e.Fermi-Dirac for electrons,Bose-Einstein for phonons,Plank for photons,etc. Non-equilibrium,e.g.in a high electric field or temperature gradient: f+v.Vf+F.Vpf= 8t f-f。 scat Relaxation Time Approximation ✉ΓK p->p Relaxation time
Boltzmann Transport Equation for Particle Transport Distribution Function of Particles: f = f(r,p,t) --probability of particle occupation of momentum p at location r and time t scat p t f f f t f v r F Relaxation Time Approximation t o f f t e Equilibrium Distribution: f0 , i.e. Fermi-Dirac for electrons, Bose-Einstein for phonons, Plank for photons, etc. Relaxation time Non-equilibrium, e.g. in a high electric field or temperature gradient: r,p p, p p p p p p p p p p f f W f W f t f o scat

Monte Carlo Solution Technique Phonons are drawn from the six individual stochastic spaces,including three wave-vector components and the three position vector components Phonons are then allowed to drift (or unrestrained motion)and scatter in time,and their statistics is collected at various points in time and space,and processed to extract the necessary information
Monte Carlo Solution Technique • Phonons are drawn from the six individual stochastic spaces, including three wave-vector components and the three position vector components • Phonons are then allowed to drift (or unrestrained motion) and scatter in time, and their statistics is collected at various points in time and space, and processed to extract the necessary information

Initial Conditions Number of phonons per unit volume and polarization(p)is usually an extremely large number A scaling factor is used to simulate only a fraction of the phonons A series of random numbers properly distributed to match the equilibrium distribution are drawn to initialize the positions, frequencies,polarizations,and wavevectors of the ensemble of phonons chosen for the simulation Mazumdar and Majumdar developed a numerical scheme to obtain the number of phonons within the ith frequency interval △oas: N;=(n(wo,i,LA)》D(wo,i,LA)△w +2(n(w0,i,TA)》D(w0,iTA)△w1
Initial Conditions • Number of phonons per unit volume and polarization (p) is usually an extremely large number • A scaling factor is used to simulate only a fraction of the phonons • A series of random numbers properly distributed to match the equilibrium distribution are drawn to initialize the positions, frequencies, polarizations, and wavevectors of the ensemble of phonons chosen for the simulation • Mazumdar and Majumdar developed a numerical scheme to obtain the number of phonons within the ith frequency interval Dw as: