
1.7反射与折射 入射波空间:E1()=E()+E,()=Emef+Emek 透射波空间:E2(G)=E,()=Eme, 问题: 入射面 E E 反射波 己知Em, 入射波 E 求解Em,Em;, 分界面 得知相应量的方向、大小? 透射波 方法:利用边界条件 导波场论 11
1.7反射与折射 导波场论 边界条件 i q r q t q z x y i E i // E i^ E 入射波 反射波 透射波 分界面 入射面 r // E r ^ E r E t ^ E t E t // E i k r k t k 入射波空间: 1( ) ( ) ( ) j ki r j kr r E r Ei r Er r Eime Erme 透射波空间: 2 ( ) ( ) j kt r E r Et r Etme 问题: 已知 Eim , ki Erm , Etm; kr , kt 求解 得知相应量的方向、大小? 方法:利用边界条件 11
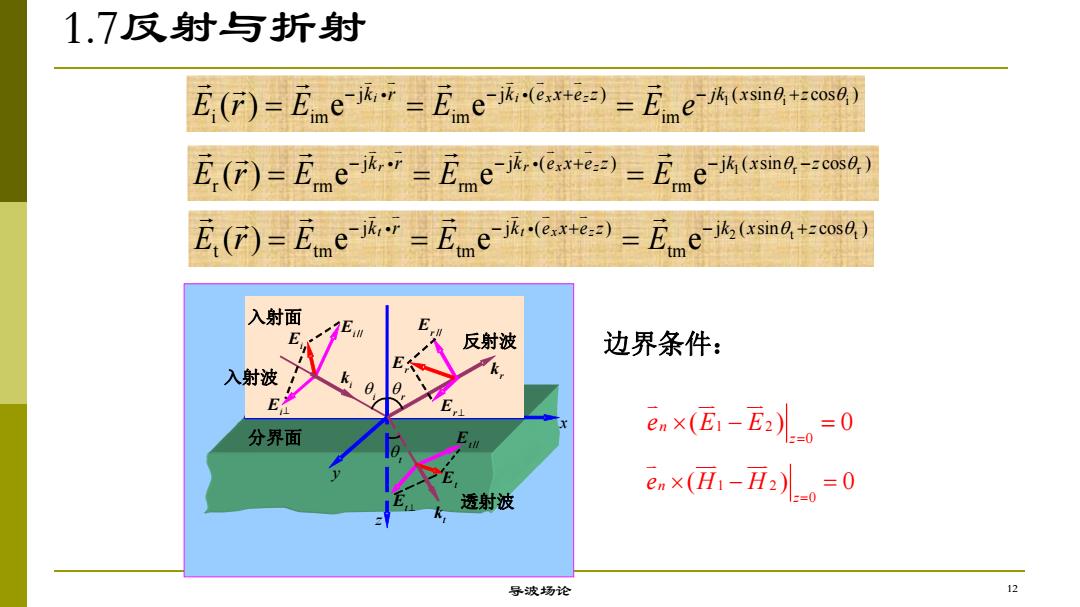
1.7反射与折射 E(f)=Eimek=Enme-etea)=Eesin+os0) E.()=Enme.r=Emej,-ex+ea)=sin8-:ca) E.()=Dne-w-Enek-en+ea)=Ene6sna+:osa 入射面 E E 反射波 边界条件: 入射波 E 分界面 enx(E1-E2)儿。=0 透射波 enx(i-F2l-。=0 导波场论
1.7反射与折射 1 i i j j ( ) ( sin cos ) i im im im ( ) e e ki r ki ex x ezz jk x z E r E E E e q q 1 r r j j ( ) j ( sin cos ) r rm rm rm ( ) e e e kr r kr ex x ezz k x z E r E E E q q 2 t t j j ( ) j ( sin cos ) t tm tm tm ( ) e e e kt r kt ex x ezz k x z E r E E E q q i q r q t q z x y Ei Ei // Ei^ 入射波 反射波 透射波 分界面 入射面 Er// Er^ Er Et^ Et Et // i k r k t k 边界条件: 1 2 0 n ( ) 0 z e E E 1 2 0 n ( ) 0 z e H H 导波场论 12
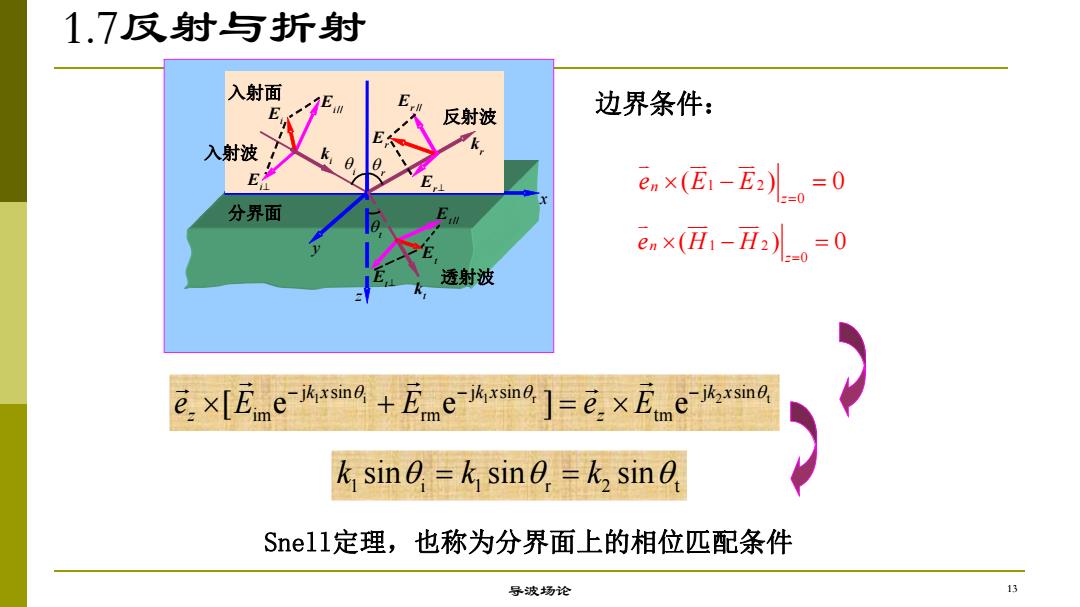
1.7反射与折射 入射面 E E E 反射波 边界条件: 入射波 E em×(E-E2L。=0 分界面 enx(H1-H2)o=O 透射波 ×[Eem9+]=×Ee-m4 rm k sine=k sine=k,sine Snell定理,也称为分界面上的相位匹配条件 导波场论 13
1.7反射与折射 导波场论 Snell定理,也称为分界面上的相位匹配条件 1 i 1 r 2 t j sin j sin j sin im rm tm [ e e ] e k x k x k x z z e E E e E q q q 1 i 1 r 2 t k sinq k sinq k sinq i q r q t q z x y Ei Ei // Ei^ 入射波 反射波 透射波 分界面 入射面 Er// Er^ Er Et^ Et Et // i k r k t k 边界条件: 1 2 0 n ( ) 0 z e E E 1 2 0 n ( ) 0 z e H H 13

1.7反射与折射 斯耐尔反射定律: 由 k sine=k sine 得: 反射角0等于入射角0: 斯耐尔折射定律: 由 k sine=k,sine 得: sine k2 k 折射角0,与入射角0,的关系 sine 式中:k=0√841,k2=0VE242 导波场论 4
1.7反射与折射 导波场论 —— 折射角 q t 与入射角 q i 的关系 —— 反射角q r 等于入射角q i 斯耐尔反射定律: 斯耐尔折射定律: 1 i 1 sin sin r 由 k q k q 得: qi qr 1 i 2 sin sin t 由 k q k q 得: i 2 t 1 sin sin k k q q 1 1 1 2 2 2 式中:k , k 14
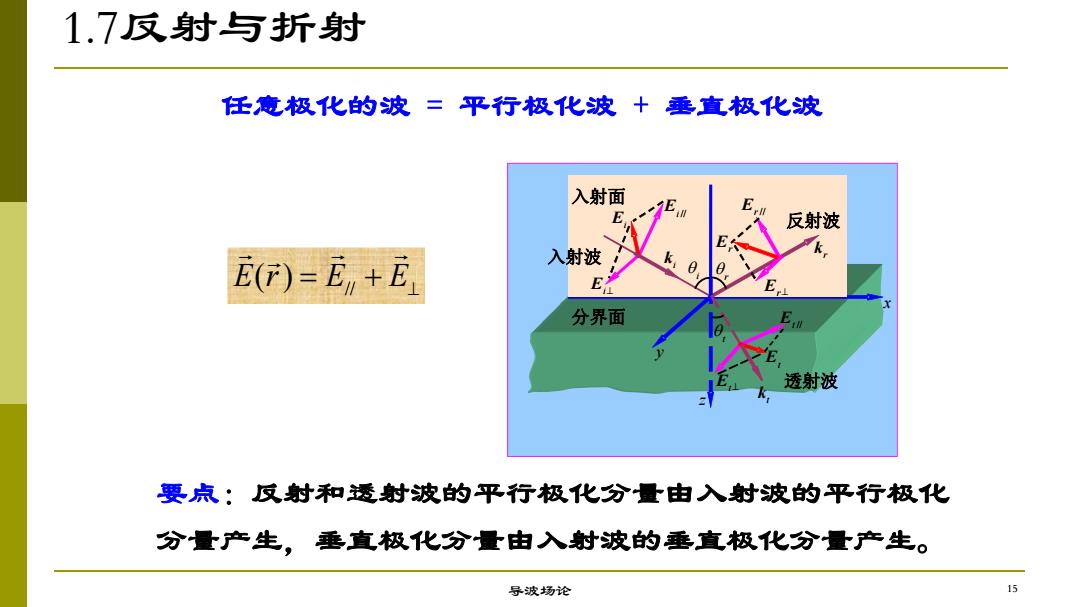
1.7反射与折射 任意极化的波=平行极化波+垂直极化波 入射面 E 反射波 E(F)=Ey+E 入射波 E 分界面 透射波 要点:反射和透射波的平行极化分量由入射波的平行极化 分量产生,垂直极化分量由入射波的垂直极化分量产生。 导波场论 15
1.7反射与折射 导波场论 任意极化的波 = 平行极化波 + 垂直极化波 要点:反射和透射波的平行极化分量由入射波的平行极化 分量产生,垂直极化分量由入射波的垂直极化分量产生。 i q r q t q z x y Ei Ei // Ei^ 入射波 反射波 透射波 分界面 入射面 Er// Er^ Er Et^ Et Et // i k r k t k // E(r) E E^ 15