《信号与系统》课程教学资源（实验指导）实验七 抽样定理

信号与系统实验指导书 实验七抽样定理 一、实验目的 1、学会运用MATLAB完成信号抽样及对抽样信号的频谱进行分析。 2、学会运用MATLAB改变抽样间隔，观察抽样后信号的频谱变化。 3、学会运用MATLAB对抽样后的信号进行重建。 二、实验原理 信号抽样就是利用抽样脉冲序列()从连续信号f()中抽取一系列的离散样值，将连 续时间信号转换为离散时间信号，也称为取样或采样，通过抽样过程得到的离散样值信号称 为抽样信号，用()表示。 f()=f)p0) 由傅立叶变换得：3U,0]=5(o)-2立Fo:P@),其中)一般为周期序列则有： Po)=2π2P.da-nms),p 1 () Ts Fs() LF(0)2x 2P.6(o-n@s)=>P.F(@-nOs) 抽样定理指出，一个有限频宽的连续时间信号f(),其最高频率为”m,经过抽样后， 只要抽样频率w,不小于信号最高频率w的两倍，即满足w,≥2wm,就能从抽样信号中恢 复源信号，得到原始信号f)。∫，()与f)相比没有失真，只有幅度和相位的的差异， 称为奈奎斯特抽样频率。当W,<2"m,将产生频谱混迭现象，则无法恢复源信号。 1、理想抽样：抽样序列为冲激序列

信号与系统实验指导书 -1- 实验七 抽样定理 一、实验目的 1、学会运用 MATLAB 完成信号抽样及对抽样信号的频谱进行分析。 2、学会运用 MATLAB 改变抽样间隔，观察抽样后信号的频谱变化。 3、学会运用 MATLAB 对抽样后的信号进行重建。 二、实验原理 信号抽样就是利用抽样脉冲序列 p(t) 从连续信号 f (t) 中抽取一系列的离散样值，将连 续时间信号转换为离散时间信号，也称为取样或采样，通过抽样过程得到的离散样值信号称 为抽样信号，用 f (t) s 表示。 f (t) f (t) p(t) s  由傅立叶变换得： ( ) ( ) 2 1 [ ( )] ( )     f s t  FS   F  P ，其中 p(t) 一般为周期序列则有：      n P Pn n S () 2  (  )， ( ) 1 ( ) 1 0 2 2   P T P t e dt T P S T T jn t S n S S S      ( ) 2 ( ) ( ) 2 1 ( ) S n S n n FS F   Pn  n P F  n              抽样定理指出，一个有限频宽的连续时间信号 f (t) ，其最高频率为 wm ，经过抽样后， 只要抽样频率 ws 不小于信号最高频率 wm 的两倍，即满足 ws  2wm ，就能从抽样信号中恢 复源信号，得到原始信号 f (t)。 f (t) s 与 f (t) 相比没有失真，只有幅度和相位的的差异， ws 称为奈奎斯特抽样频率。当 ws  2wm ，将产生频谱混迭现象，则无法恢复源信号。 1、理想抽样：抽样序列为冲激序列

信号与系统实验指导书 ,0emh= Fs(@)=1>F(o-n0s) 7。 1Pe)=6(④ P(@) -m f) F() f:(C Fs(a) -s -四g0 1、矩形脉冲抽样 2 Ro-2RRa-na-三学ra-na 三、实验内容 该信号经冲激脉冲抽样后得到的抽样信号及其频谱，抽样间隔T(s)=1。 程序如下： Ts=1; dt-0.上， t1=-4:dt4 2

信号与系统实验指导书 -2-       n T nTS P(t)  (t)  (t ) S T T jn t T S n T t e dt T P S S S 1 ( ) 1 2 2             n S S S F n T F ( ) 1 ()   1、 矩形脉冲抽样 ) 2 ( ) ( 1 ) 2 ( ) ( 0 0        S S S n n S a T A P T P  A S a P   ) ( ) 2 ( ) ( ) ( S n S n S s n S F n n S a T A F P F n                   三、实验内容 【例 7-1】已知升余弦脉冲信号为               2 1 cos 2 1 ( ) t f t ，0  t   ，用 MATLAB 实现 该信号经冲激脉冲抽样后得到的抽样信号及其频谱，抽样间隔 T(s) 1。 程序如下： Ts=1; dt=0.1; t1=-4:dt:4;

信号与系统实验指导书 f=((1+cos(t1))/2).*(u(tl+pi)-u(t1-pi)). subplot(221); plot(tI,ft); grid on; axis[-44-0.11.1 xlabel("Time(sec)); ylabel(ft)). title(升余弦脉冲信号)方 N=500: k=-N:N: W=pi*k/(N*dt); Fw=dt*ft*exp(-j*tl'*W) subplot(222): plot(W.abs(Fw)): grid on axis(-1010-0.21.1*pi]) xlabel("omega) ylabel(Fw): ttc(升余弦脉冲信号的频谱)： 2=.4:Ts4 fst=((l+cos(t2))/2).*(u(t2+pi)-u(t2-pi)). subplot(223); plot(tl,'"方 hold on stem(t2.fst). grid on axis-44-0.11.1]D xlabel("Time(sec)); ylabel('fs(t)); tile(抽样后信号； hold off Fsw=Ts*fst*exp(-j*t2"W): subplot(224). plot(W.abs(Fsw)). grid on axis-1010-0.21.1*pi] xlabel(\omega):

信号与系统实验指导书 -3- ft=((1+cos(t1))/2).*(u(t1+pi)-u(t1-pi)); subplot(221); plot(t1,ft); grid on; axis([-4 4 -0.1 1.1]); xlabel('Time(sec)'); ylabel('f(t)'); title('升余弦脉冲信号'); N=500; k=-N:N; W=pi*k/(N*dt); Fw=dt*ft*exp(-j*t1'*W); subplot(222); plot(W,abs(Fw)); grid on axis([-10 10 -0.2 1.1*pi]); xlabel('\omega'); ylabel('Fw'); title('升余弦脉冲信号的频谱'); t2=-4:Ts:4; fst=((1+cos(t2))/2).*(u(t2+pi)-u(t2-pi)); subplot(223); plot(t1,ft,':'); hold on stem(t2,fst); grid on axis([-4 4 -0.1 1.1]); xlabel('Time(sec)'); ylabel('fs(t)'); title('抽样后信号'); hold off Fsw=Ts*fst*exp(-j*t2'*W); subplot(224); plot(W,abs(Fsw)); grid on axis([-10 10 -0.2 1.1*pi]); xlabel('\omega');

信号与系统实验指导书 ylabel('Fs(w)): tile(抽样后信号的频谱) 程序运行后，波形如图7-1所示。 升余弦脉冲信号 升余弦脉冲信号的频谱 1 / e0.5 0 2 5 抽样后信号 抽样后信号的频谱 / 号0.5 0 =4 2 0 2 4 -10 5 图71信号抽样后频谱 针对上述波形，如果修改抽样间隔分别进行抽样，可得到如下波形

信号与系统实验指导书 -4- ylabel('Fs(w)'); title('抽样后信号的频谱') 程序运行后，波形如图 7-1 所示。 针对上述波形，如果修改抽样间隔分别进行抽样，可得到如下波形。 图 7-1 信号抽样后频谱

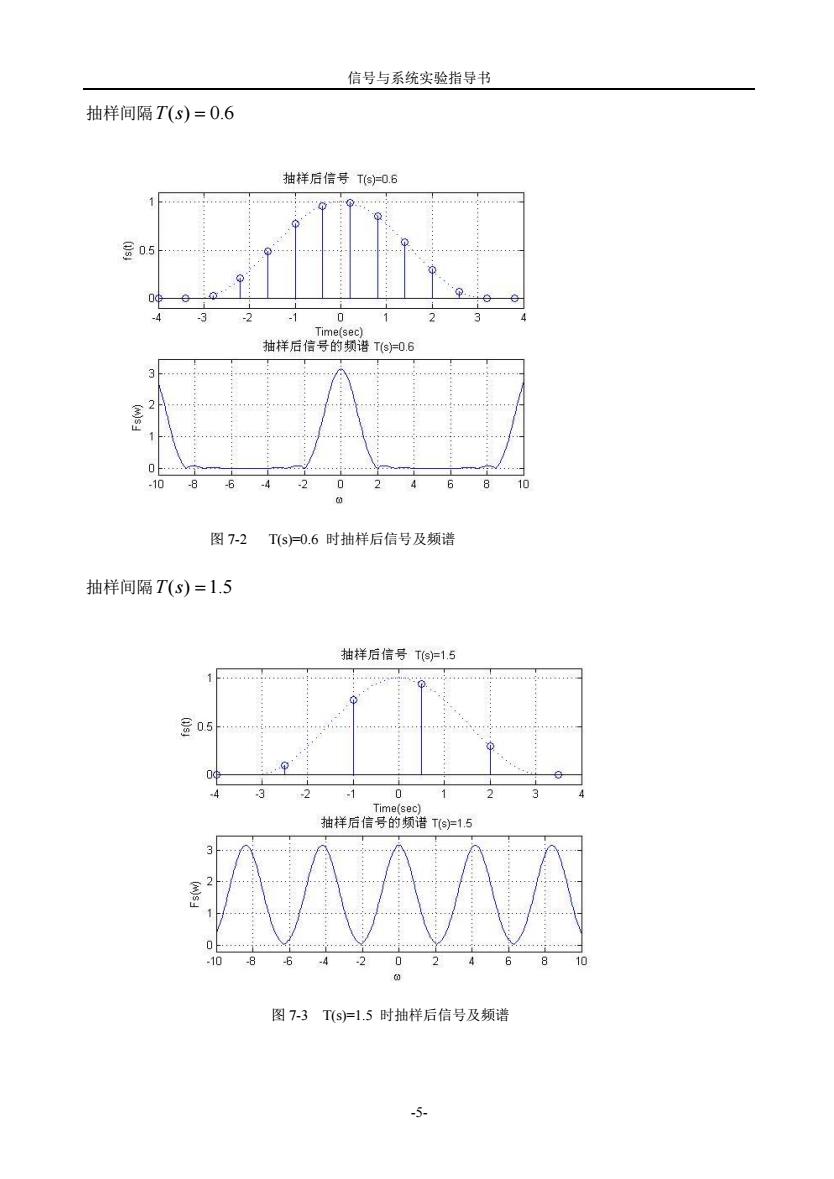
信号与系统实验指导书 抽样间隔T(s)=0.6 抽样后信号Ts06 1 。 0 -4 3 2 -1 2 抽样后信号的频谱T0.E 图7-2Ts=0.6时抽样后信号及颍诺 抽样间隔T(s)=1.5 抽样后信号T1.5 忌05 3 抽样后信号的频话T15 864-2 0 2468 图7-3T(s=1.5时抽样后信号及频诺

信号与系统实验指导书 -5- 抽样间隔 T(s)  0.6 抽样间隔 T(s) 1.5 图 7-2 T(s)=0.6 时抽样后信号及频谱 图 7-3 T(s)=1.5 时抽样后信号及频谱