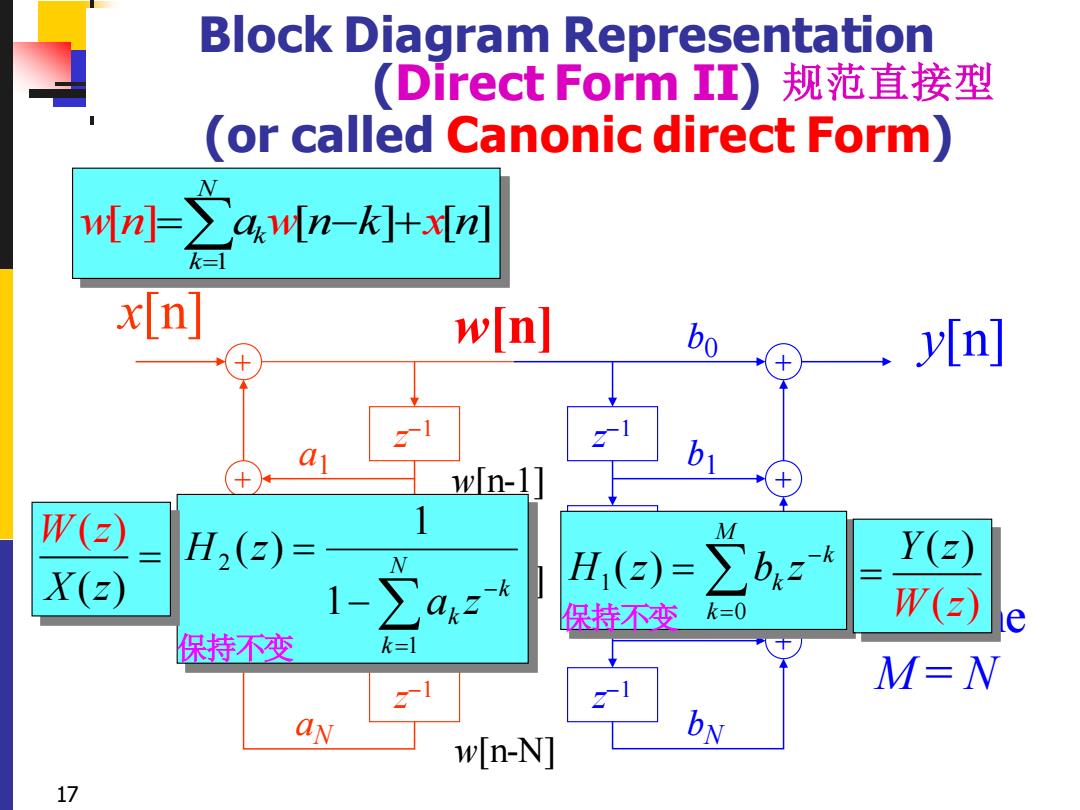
Block Diagram Representation (Direct Form II)规范直接型 (or called Canonic direct Form) fml-之an-]+xn] k=1 xn wn] bo y[n] wIn-1] W(z) H,(2)= X(2) 1-∑a4z H,(2)=∑bz Y() 保持不变 k=0 W(2) e 保持不变 k=1 21 M=N N w[n-N] bN 17
17 Block Diagram Representation (Direct Form II) + z −1 z −1 + z −1 + b0 b1 bN−1 bN x[n] + z −1 z −1 + z −1 + a1 aN−1 aN y[n] w[n-1] w[n-2] w[n-N] Assume M = N = − = M k k k H z b z 0 1 ( ) = − − = N k k k a z H z 1 2 1 1 ( ) (or called Canonic direct Form) ( ) ( ) Y z W z = ( ( ) ) X W z z = w[n] 规范直接型 保持不变 保持不变 1 [ ] [ ] [ ] N k k wn a n k n w x = = − +
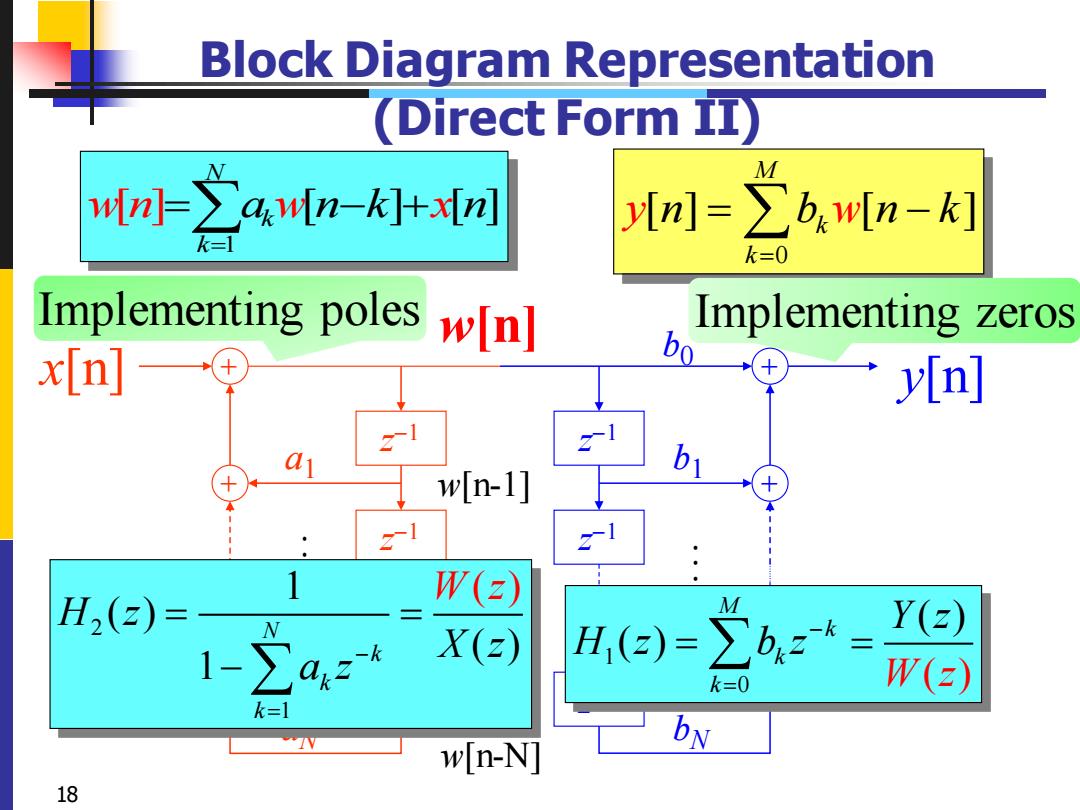
Block Diagram Representation (Direct Form II) M n]∑an-]+xJ y[n=∑bw[n-k] k=1 k=0 Implementing poles w[n] Implementing zeros x[n] bo y[n] w[n-1] 21 W(z) H2(2)= Y() 1-∑az X(2) H,(a)=∑bz= k=0 W(2) k=1 w[n-N] bN 18
18 + z −1 z −1 + z −1 + b0 b1 bN−1 bN x[n] + z −1 z −1 + z −1 + a1 aN−1 aN y[n] w[n-1] w[n-2] w[n-N] w[n] Assume M = N . . . . . . Block Diagram Representation (Direct Form II) 1 0 ( ) ( ) ( ) M k k k W z Y z H z b z− = = = 2 1 1 ( ) ( ) ( ) 1 N k k k H z X z a W z z − = = = − 0 [ ] [ ] M k k y w n b n k = [ ] 1 [ ] [ ] = − N k k wn a n k n w x = = − + Implementing poles Implementing zeros
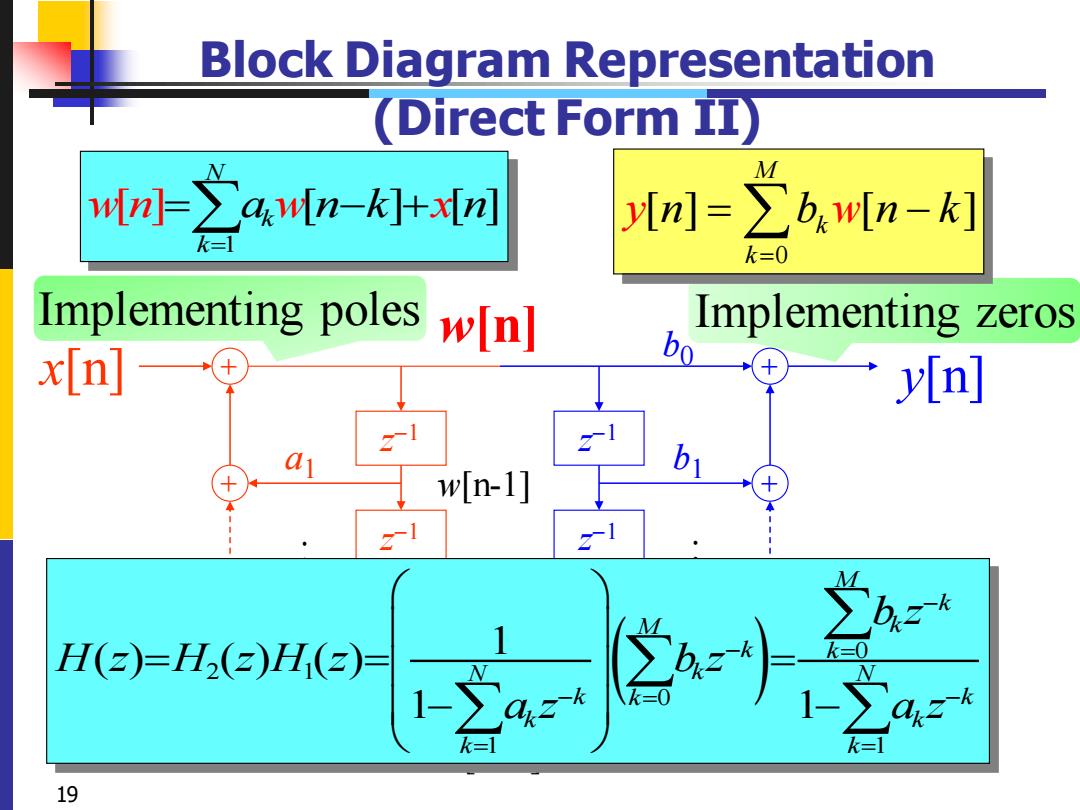
Block Diagram Representation (Direct Form II) M wn-∑an-+xJ y[n]=∑b:w[n-k] k=1 k=0 Implementing poles wn] Implementing zeros x[n] bo y[n] 21 w[n-1] 1 M H(z)=H2(2)H(2Z)= 1-2 k=1 19
19 + z −1 z −1 + z −1 + b0 b1 bN−1 bN x[n] + z −1 z −1 + z −1 + a1 aN−1 aN y[n] w[n-1] w[n-2] w[n-N] w[n] Assume M = N . . . . . . Block Diagram Representation (Direct Form II) 1 0 ( ) ( ) ( ) M k k k W z Y z H z b z− = = = 2 1 1 ( ) ( ) ( ) 1 N k k k H z X z a W z z − = = = − Implementing poles Implementing zeros ( ) 0 2 1 0 1 1 1 ( ) ( ) ( ) 1 1 M k M k k k N N k k k k k k k k b z H z H z H z b z a z a z − − = − − = = = = = = − − 0 [ ] [ ] M k k y w n b n k = [ ] 1 [ ] [ ] = − N k k wn a n k n w x = = − +

Block Diagram Representation (Direct Form II) How many Adders? N+M 与交换前相比 How many multipliers? N+M+1 无变化 How many delays? N+M x[n] wn bo y[n] a w[n-1] w[n-2] aN-1 bN-1 Assume M=N w[n-N] bN 21
21 Block Diagram Representation (Direct Form II) How many Adders? How many multipliers? How many delays? + z −1 z −1 + z −1 + b0 b1 bN−1 bN x[n] + z −1 z −1 + z −1 + a1 aN−1 aN y[n] w[n-1] w[n-2] w[n-N] w[n] Assume M = N . . . . . . N N N+M +M +M+1 与交换前相比 无变化
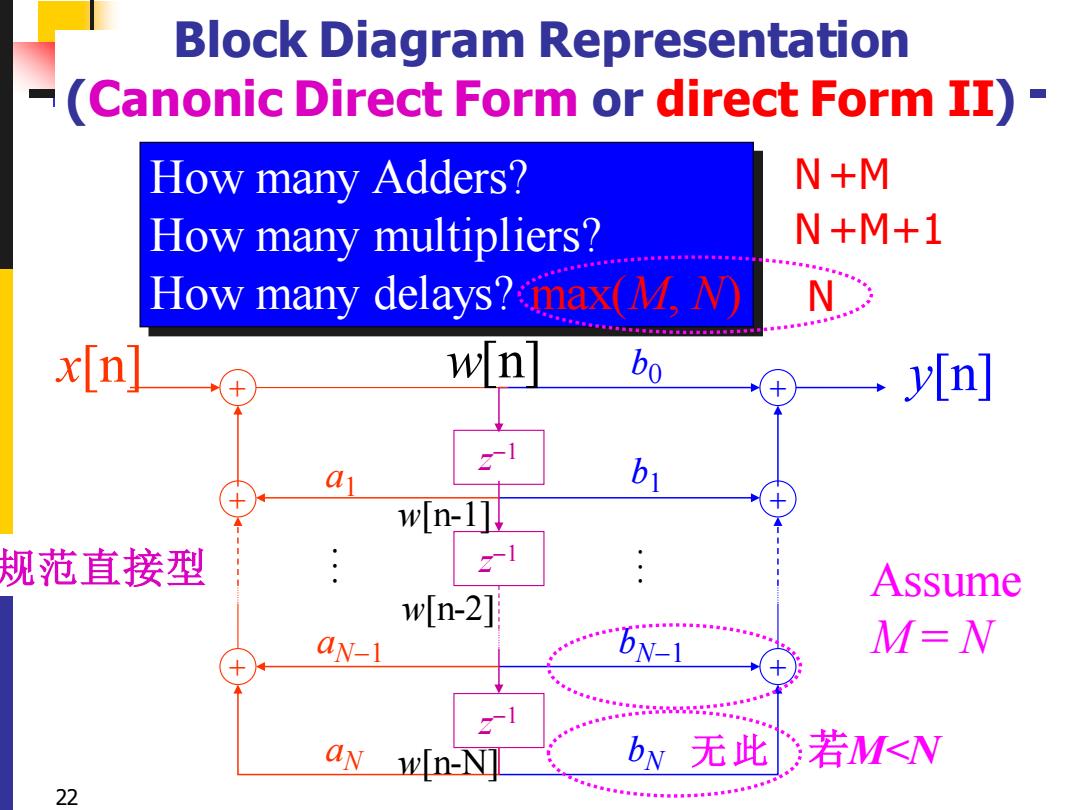
Block Diagram Representation (Canonic Direct Form or direct Form II)- How many Adders? N+M How many multipliers? N+M+1 How many delays?max(M,N) N x[nl w n bo y[n] wn-1 规范直接型 Assume w[n-2] an-1 W-1 M=N wIn-NI bN无此 若M<N 22
22 Block Diagram Representation (Canonic Direct Form or direct Form II) How many Adders? How many multipliers? How many delays? max(M, N) + + + b0 b1 bN−1 bN x[n] + z −1 z −1 + z −1 + a1 aN−1 aN y[n] N N +M +M+1 N w[n-1] w[n-2] w[n-N] Assume M = N w[n] 规范直接型 无此 若M<N . . . . . . (Canonic Direct Form or direct Form II) 规范直接型