《电力系统分析》课程教学课件（讲稿）09 电力系统三相短路电流的实用计算

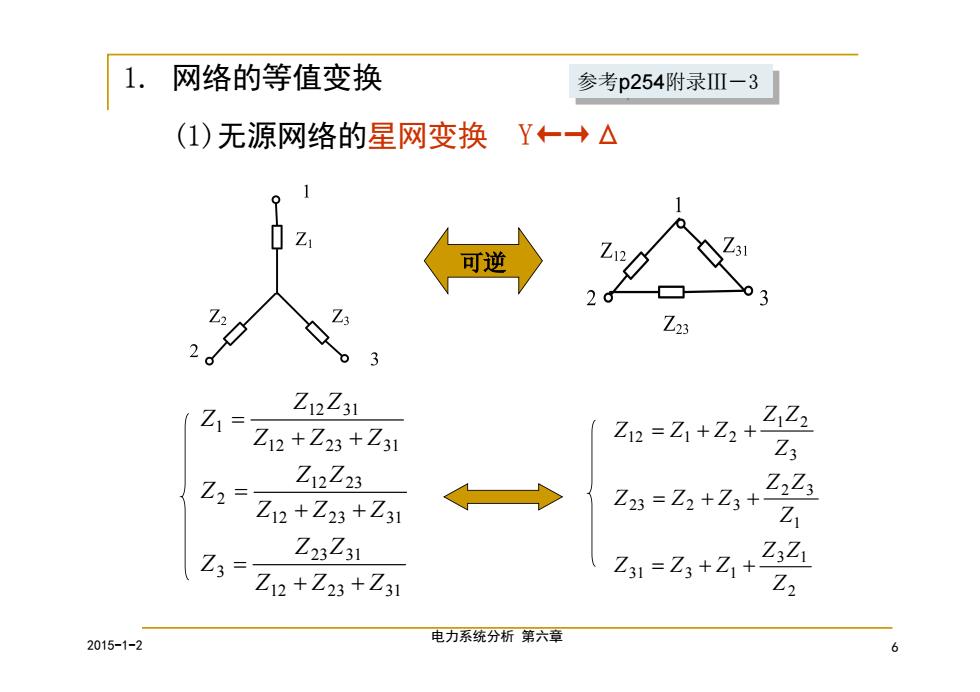
1. 网络的等值变换 参考p254附录IⅢ-3 (1)无源网络的星网变换Y←→△ 可逆 26 Z23 2。 ZI= Z12Z31 12+Z23+Z31 Z12=Z1+Z2+ ZiZ2 Z2= Z12Z23 Z23=Z2+Z3+ Z2Z3 Z12+Z23+Z31 Z Z3= Z23Z31 Z:Zi Z12+Z23+Z31 Z31=Z3+Z1+ Z2 2015-1-2 电力系统分析第六章 6

2015-1-2 电力系统分析 第六章 6 1. 网络的等值变换 (1)无源网络的星网变换 可逆 12 23 31 23 31 3 12 23 31 12 23 2 12 23 31 12 31 1 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z          2 3 1 31 3 1 1 2 3 23 2 3 3 1 2 12 1 2 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z          Y←→Δ 参考参考p254附录Ⅲ－3 p254附录Ⅲ－3

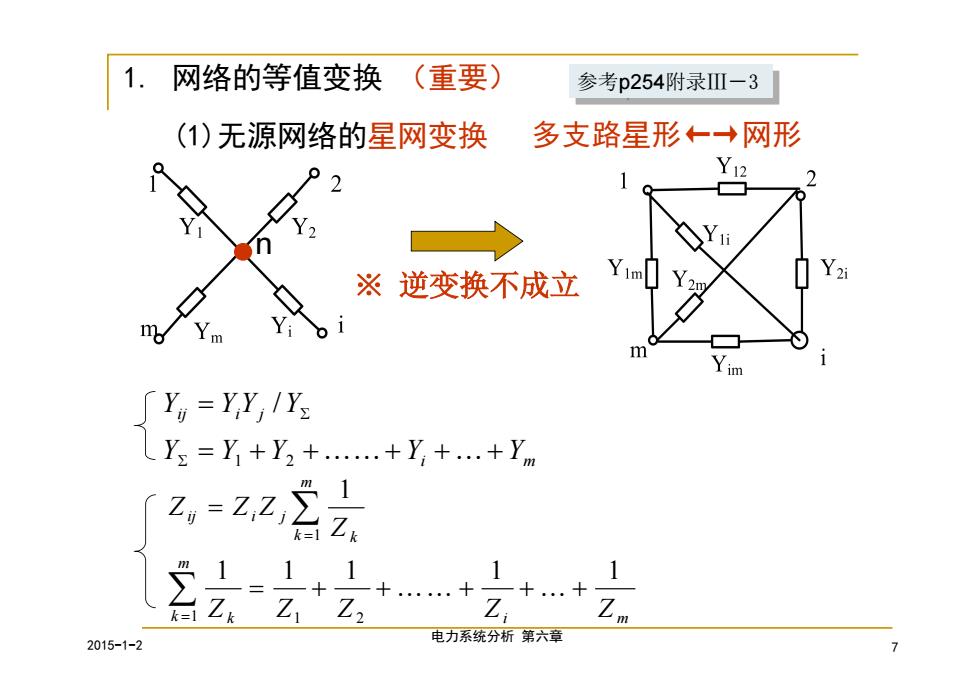
1. 网络的等值变换 (重要) 参考p254附录Ⅲ-3 (1)无源网络的星网变换 多支路星形←→网形 12 ※逆变换不成立 Yim Ym Y=YY,IYs 人Y2=Y+Y2+.+Y,+.+Ym 1 +.+ +.十 ZZ Z, Zm 2015-1-2 电力系统分析第六章 >

2015-1-2 电力系统分析 第六章 7 多支路星形←→网形 ※ 逆变换不成立 1. 网络的等值变换 （重要） (1)无源网络的星网变换 i m m k k m k k ij i j Z Z Z Z Z Z Z Z Z 1 1 1 1 1 1 1 1 2 1              i m ij i j Y Y Y Y Y Y Y Y Y          1 2   / n 参考参考p254附录Ⅲ－3 p254附录Ⅲ－3

证明：星网变换 参考p254附录Ⅲ-3 基尔霍夫定律，对于n节点有： g.-0-2xaa)-0 k=1 YΣ：以节点n为中心的星形电路所有支路导纳之和。 2015-1-2 电力系统分析第六章

2015-1-2 电力系统分析 第六章 8 证明：星网变换 n 基尔霍夫定律，对于n节点有：                 Y Y u Y Y u u I Y u u m k k k m k k m k k k n m k k k n m k kn 1 1 1 1 1 0 ( ) 0       YΣ:以节点n为中心的星形电路所有支路导纳之和。 参考参考p254附录Ⅲ－3 p254附录Ⅲ－3

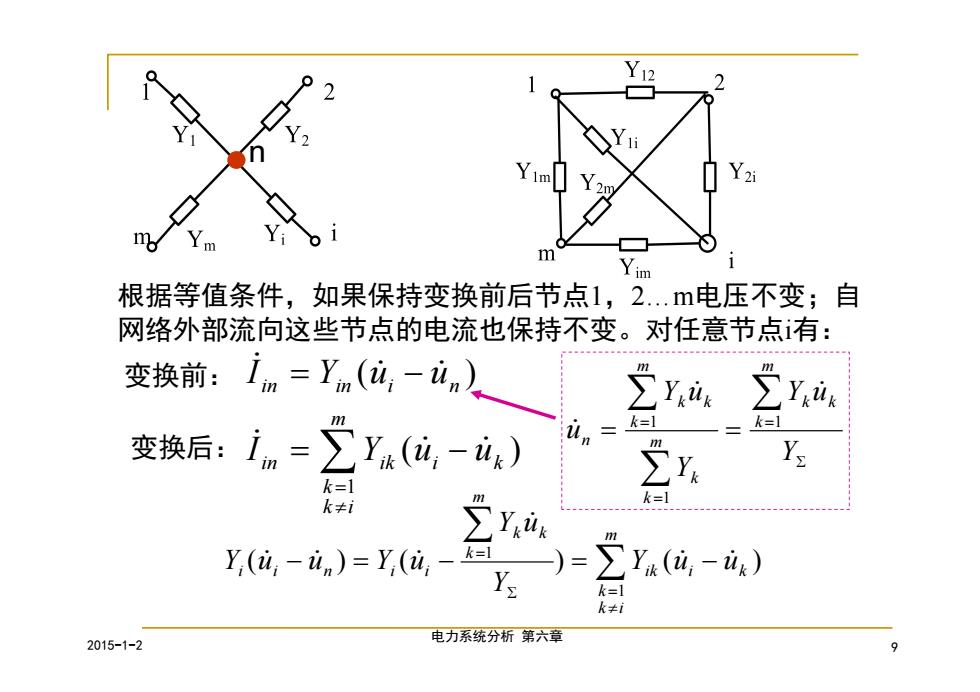
m 根据等值条件，如果保持变换前后节点1,2.m电压不变；自 网络外部流向这些节点的电流也保持不变。对任意节点有： 变换前：in=Yn(u,-un) ,4 k=1 变换后： in=∑y(a,-i) un = Y k=1 y. k=1 k≠i Y(u-in)=Y(i Y Yu (u-ug) k=1 k≠i 2015-1-2 电力系统分析第六章

2015-1-2 电力系统分析 第六章 9 n 根据等值条件，如果保持变换前后节点1，2.m电压不变；自 网络外部流向这些节点的电流也保持不变。对任意节点i有： ( ) ( ) 1 i k m k i k in ik in in i n I Y u u I Y u u              ( ) ( ) ( ) 1 1            m k i k ik i k m k k k i i n i i Y u u Y Y u Y u u Y u       变换前： 变换后：          Y Y u Y Y u u m k k k m k k m k k k n 1 1 1   

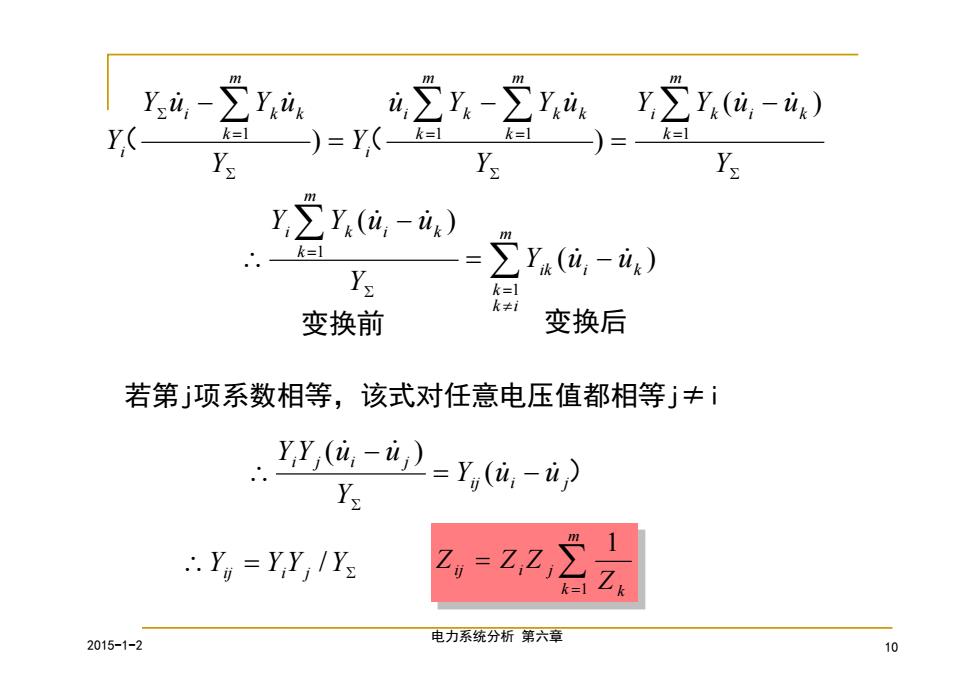
ram-Yam n2r-ri r.2r(u-i) Y( k=1 )=Y(L k=1 k=1 Y y∑y(位，-) k=1 Y 变换前 变换后 若第j项系数相等，该式对任意电压值都相等j丰1 .Ya-2=y,(a,-） Y .Y=YY,IYs 2=2,2 2015-1-2 电力系统分析第六章 10

2015-1-2 电力系统分析 第六章 10                 Y Y Y u u Y u Y Y u Y Y Y u Y u Y i k m k i k m k k k m k i k i m k i k k i ( ) ) ) 1 1 1 1       （ （ ( ) ( ) 1 1           m k i k ik i k i k m k i k Y u u Y Y Y u u     变换前 变换后 若第j项系数相等，该式对任意电压值都相等j≠i ij i j） i j i j Y u u Y Y Y u u          ( ( ) Yij  YiYj Y /   m k k ij i j Z Z Z Z 1 1