第3章静态电兹场及其边值问题的解 21 1.电容 电容是导体系统的一种基本属性,是描述导体系统储存电荷能 力的物理量。 孤立导体的电容 孤立导体的电容定义为所带电量q与其电位φ的比值,即 C=9 9=U 0 \p,=0 两个带等量异号电荷(士q)的 导体组成的电容器,其电容为 C-9 q U 01-p2 电容的大小只与导体系统的几何尺寸、形状和及周围电介质 的特性参数有关,而与导体的带电量和电位无关。 >>I
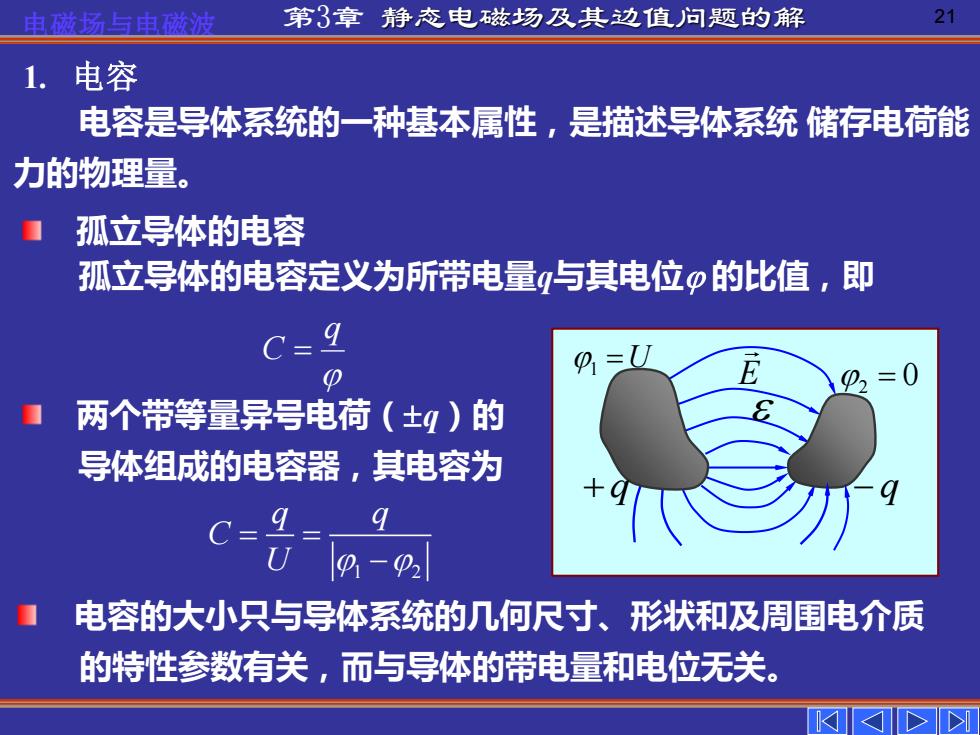
电磁场与电磁波 第3章 静态电磁场及其边值问题的解 21 电容是导体系统的一种基本属性,是描述导体系统 储存电荷能 力的物理量。 孤立导体的电容定义为所带电量q与其电位 的比值,即 q C = 1. 电容 孤立导体的电容 两个带等量异号电荷(q)的 导体组成的电容器,其电容为 1 2 q q C U = = − 电容的大小只与导体系统的几何尺寸、形状和及周围电介质 的特性参数有关,而与导体的带电量和电位无关。 E 2 = 0 1 =U + q − q

电磁场与电磁波 第3章静态电兹场及其边值问题的解 22 ■计算电容的方法一: (1)假定两导体上分别带电荷+q和-q; (2)计算两导体间的电场强度E: ③)由0=Ed,求出两导体间的电位差; (4)求比值C=q/U,即得出所求电容。 计算电容的方法二: (1)假定两电极间的电位差为U; (2)计算两电极间的电位分布0, (③)由E=-Vo得到E; (4)由Ps=EEn得到Ps; ⑤)由q=P,dS,求出导体的电荷g; (6)求比值C=q/U,即得出所求电容
电磁场与电磁波 第3章 静态电磁场及其边值问题的解 22 (1) 假定两导体上分别带电荷+q 和-q ; 计算电容的方法一: (4) 求比值 C = q U ,即得出所求电容。 = 2 1 E dl (3) 由 U ,求出两导体间的电位差; (2) 计算两导体间的电场强度E; 计算电容的方法二: (1) 假定两电极间的电位差为U ; (4) 由 得到 ; S En = S (2) 计算两电极间的电位分布 ; E = − (3) 由 得到E ; = S S (5) 由 q dS ,求出导体的电荷q ; (6) 求比值 C = q U,即得出所求电容

电磁场与电派 第3章静态电磁场及其边值问题的解 23 例3.1,4同心球形电容器的内导体半径为a、外导体半径为b,其 间填充介电常数为的均匀介质。求此球形电容器的电容。 解:设内导体的电荷为q,则由高斯定理可求得内外导体间 的电场 D =e 4元1 同心导体间的电压 q b-a 4元60 ab 球形电容器的电容 C= 4π8,ab U b-a 当b时 C=4π8a◆ 孤立导体球的电容 KKDH
电磁场与电磁波 第3章 静态电磁场及其边值问题的解 23 解:设内导体的电荷为q ,则由高斯定理可求得内外导体间 的电场 4π 4π r r 2 2 q q D e , E e r r = = 0 0 1 1 d ( ) 4π 4π b a q q b a U E r a b ab − = = − = 同心导体间的电压 0 q 4π ab C U b a = = − 球形电容器的电容 C a 4π 0 当 b → 时, = 例3.1.4 同心球形电容器的内导体半径为a 、外导体半径为b,其 间填充介电常数为ε的均匀介质。求此球形电容器的电容。 孤立导体球的电容 a b o
电诚场与电磁波 第3章静态电兹场及其边值问题的解 24 例3.1.5如图所示的平行双线传输线,导线半径为α,两导线 的轴线距离为D,且D>α,求传输线弹位长度的电容。 解设两导线单位长度带电量分别为+p和-P。由于D>a 故可近似地认为电荷分别均匀分布在两 导线的表面上。应用高斯定理和叠加原 理,可得到两导线之间的平面上任一点 P的电场强度为 E(x)=e 2元80 D- 两导线间的电位差 D-a D dx= 故单位长度的电容为G= 兀eo (F/m) U In[(D-a)/a]In(D/a)
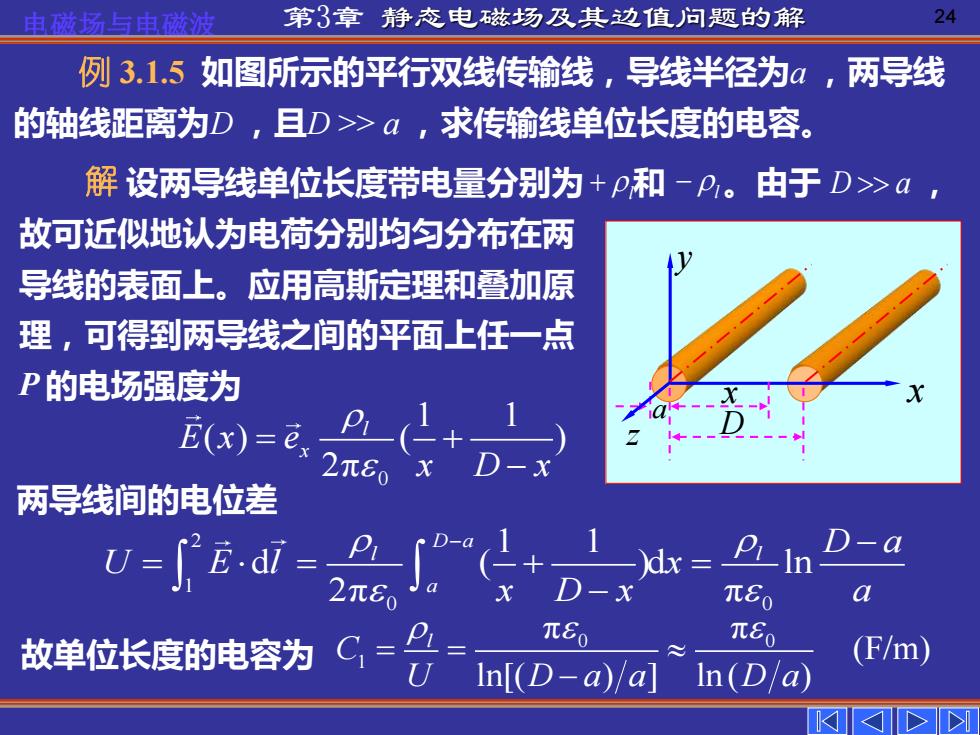
电磁场与电磁波 第3章 静态电磁场及其边值问题的解 24 例 3.1.5 如图所示的平行双线传输线,导线半径为a ,两导线 的轴线距离为D ,且D >> a ,求传输线单位长度的电容。 解 设两导线单位长度带电量分别为 + l 和 。由于 , 故可近似地认为电荷分别均匀分布在两 导线的表面上。应用高斯定理和叠加原 理,可得到两导线之间的平面上任一点 P 的电场强度为 − l D a 0 1 1 ( ) ( ) 2π l E x ex x D x = + − 两导线间的电位差 2 1 0 0 1 1 d ( )d ln 2π π D a l l a D a U E l x x D x a − − = = + = − 故单位长度的电容为 0 0 1 π π (F/m) ln[( ) ] ln ( ) l C U D a a D a = = − x y z x D a

电破场与申 第3章静态电滋场及其边值问题的解 25 例3.1.6同轴线内导体半径为a,外导体半径为b,内外导体 间填充的介电常数为ε的均匀介质,求同轴线单位长度的电容。 解设同轴线的内、外导体单位长度带电量分别为+P和一P, 应用高斯定理可得到内外导体间任一点的电场强度为 E(p)=@ 2πp 内外导体间的电位差 =ep元 同轴线 PLln(bla) 2元8 故得同轴线单位长度的电容为℃=A 2π8 (F/m) In(b/a)
电磁场与电磁波 第3章 静态电磁场及其边值问题的解 25 例3.1.6 同轴线内导体半径为a ,外导体半径为b ,内外导体 间填充的介电常数为 的均匀介质,求同轴线单位长度的电容。 ( ) 2π l E e = 内外导体间的电位差 1 ( ) d d 2π b b l a a U E e = = 解 设同轴线的内、外导体单位长度带电量分别为 + l 和 − l , 应用高斯定理可得到内外导体间任一点的电场强度为 故得同轴线单位长度的电容为 1 2π (F/m) ln( / ) l C U b a = = a b 同轴线 ln( / ) 2π l b a =