
第8章土压力理论 静止土压力系数K的确定 经验公式法: 式中 KoR =JOCR(1-sin p') KoR一超固结土的静止土压力系数 OCR一土的超固结比; 查表法: 静止土压力分布沿墙高呈三角形分布。 静止土压力系数值 若墙高为H,则作用于单位长度墙上的总静 土名 K 止土压力E为三角形的面积,即 砾石、卵石 0.20 砂土 0.25 亚砂土 0.35 亚粘土 0.45 粘土 0.55 E的作用点在距离墙地面高的H3处。 土质学与土力学 6211 吉林大学建设工程学院
土质学与土力学 62—11 吉林大学建设工程学院 静止土压力分布沿墙高呈三角形分布。 若墙高为H,则作用于单位长度墙上的总静 止土压力E0为三角形的面积,即 Eo的作用点在距离墙地面高的H/3处。 2 0 0 2 1 E = K H 静止土压力系数K0的确定 查表法: 经验公式法: 静止土压力系数值 土 名 K0 砾石、卵石 砂 土 亚砂土 亚粘土 粘 土 0.20 0.25 0.35 0.45 0.55 (1 sin ) K0 = OCR − R 式中 K0R ⎯超固结土的静止土压力系数 OCR⎯土的超固结比;

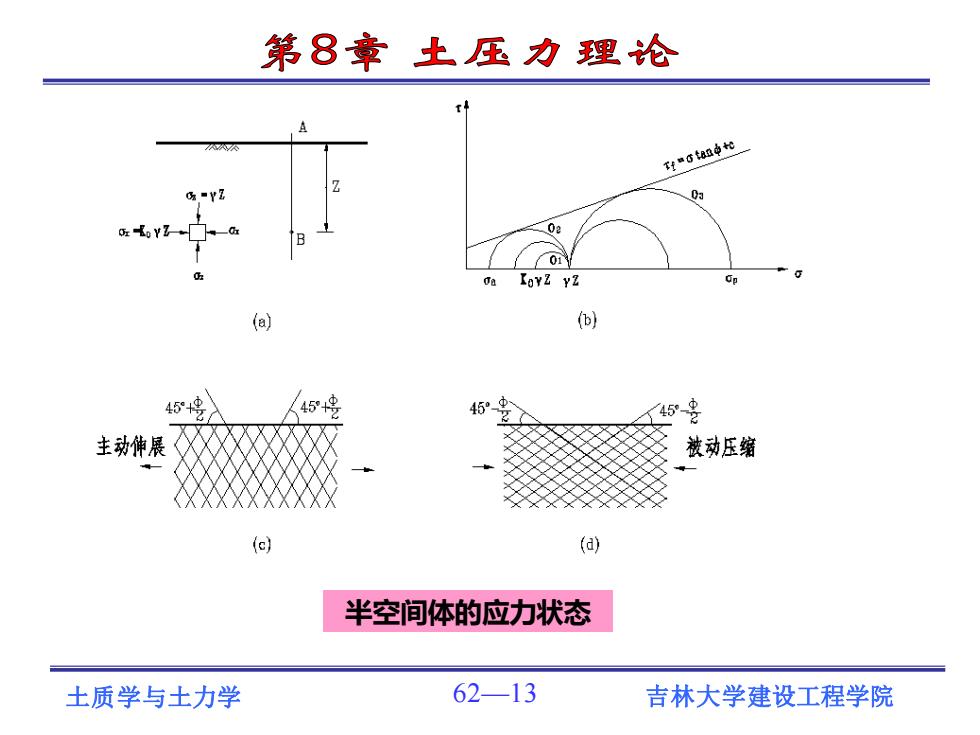
第8章土压力理论 第4节朗肯土压力理论 朗肯土压力理论基础:半空间体的应力状态和土的极限平衡理论 朗肯土压力理论基本假设: 墙背直立、光滑,墙后填土面水平;先做墙后填土。 墙背与填土界面上的剪应力为零,不改变右边土体中的应力状 态。当挡土墙的位移符合上述主动或被动极限平衡条件时,作用 在挡土墙墙背上的土压力即为朗肯主动土压力或朗肯被动土压力 0 土质学与土力学 62-12 吉林大学建设工程学院
土质学与土力学 62—12 吉林大学建设工程学院 朗肯土压力理论基础:半空间体的应力状态和土的极限平衡理论 墙背与填土界面上的剪应力为零,不改变右边土体中的应力状 态。当挡土墙的位移符合上述主动或被动极限平衡条件时,作用 在挡土墙墙背上的土压力即为朗肯主动土压力或朗肯被动土压力 。 第4节 朗肯土压力理论 朗肯土压力理论基本假设: 墙背直立、光滑,墙后填土面水平;先做墙后填土
第8章土压力理论 对*Gaa海地 0时 0: 019 a【OYZ YZ (m) () 45 45+9 45° 主动伸展 被动压缩 (c) (d) 半空间体的应力状态 土质学与土力学 62-13 吉林大学建设工程学院
土质学与土力学 62—13 吉林大学建设工程学院 半空间体的应力状态

第8章土压力理论 主动土压力计算 大主应力 01=0=Y 主动土压力状 态下的应力 小主应力 03 =Oh ka 主动土压力强度g=Gka 可以得到 .=m(45”-分-2ca45”-号 Oa=zK。-2c√K。 K。一朗肯主动士压力系数, Y土的重度: 土质学与土力学 62-14 吉林大学建设工程学院
土质学与土力学 62—14 吉林大学建设工程学院 主动土压力计算 大主应力 1 = v =z 小主应力 3 = h ka 主动土压力强度 a = h ka 主动土压力状 态下的应力 a a a o o a zK c K z c 2 ) 2 ) 2 tan(45 2 tan (45 2 = − = − − − 可以得到 Ka —朗肯主动土压力系数, —土的重度;

第8章土压力理论 对于无粘性土 ,=am'(45”-3)=K。 主动土压力的合力 Ea MH2K。 2 合力作用点在三角形的重心处,即在挡土墙墙底以上3处。 土质学与土力学 62-15 吉林大学建设工程学院
土质学与土力学 62—15 吉林大学建设工程学院 对于无粘性土 a o a z zK = − ) = 2 tan (45 2 主动土压力的合力 Ea H Ka 2 2 1 = 合力作用点在三角形的重心处,即在挡土墙墙底以上H/3处