
第8章土压力理论 粘性土的主动土压力强 度包括两部分: 1.土自重引起zK。 +】 2.粘聚力c引起2cK,12 -(H-z0) -YHK- YHK.-2cVK, 负侧压力对墙背产生拉应力,但在很小的拉力作用下就会分离(一般情况下 认为土不能承受拉应力),故计算时,这部分可忽略。 临界深度石 zoK。-2cVK。=0,→。= 2c 粘性土主动土压力 E,=K。-21vK+20 E,作用点位于墙底 以上(H-)/3处 土质学与土力学 62-16 吉林大学建设工程学院
土质学与土力学 62—16 吉林大学建设工程学院 粘性土的主动土压力强 度包括两部分: 1. 土自重引起γzKa 2. 粘聚力c引起2cKa 1/2 临界深度z0 a a a K c z K c K z 2 2 0, 0 − = 0 = 2 2 2 2 2 1 c Ea = H Ka − cH Ka + 负侧压力对墙背产生拉应力,但在很小的拉力作用下就会分离(一般情况下 认为土不能承受拉应力),故计算时,这部分可忽略。 粘性土主动土压力 Ea作用点位于墙底 以上(H-z0 )/3处

第8章土压力理论 【例题8-1】有8m高的直立挡土墙,填土的指标为y=l8kN/m3,c=20kPa,p= 12°,求作用在墙背上的朗肯主动土压力值。 解:(1)朗肯主动土压力系数: K.=tan2(45°-12°/2)=0.656 √Ka=0.810 (2)受拉区高度: 2c =2×20=2.74m yVK。18×0.81 H-x=8-2.74=5.26m (3)作用在墙背底面之=8m处的主动土压力强度: oa=yzK。-2c√Ka=18×8×0.656-2×20×0.81=62.1kPa (4)主动土压力合力: E。=号×62.1×5.26=163.3kN/m 合力作用点距墙底距离为5.26/3=1.75m 土质学与土力学 62-17 吉林大学建设工程学院
土质学与土力学 62—17 吉林大学建设工程学院 合力作用点距墙底距离为 5.26 / 3 = 1.75m
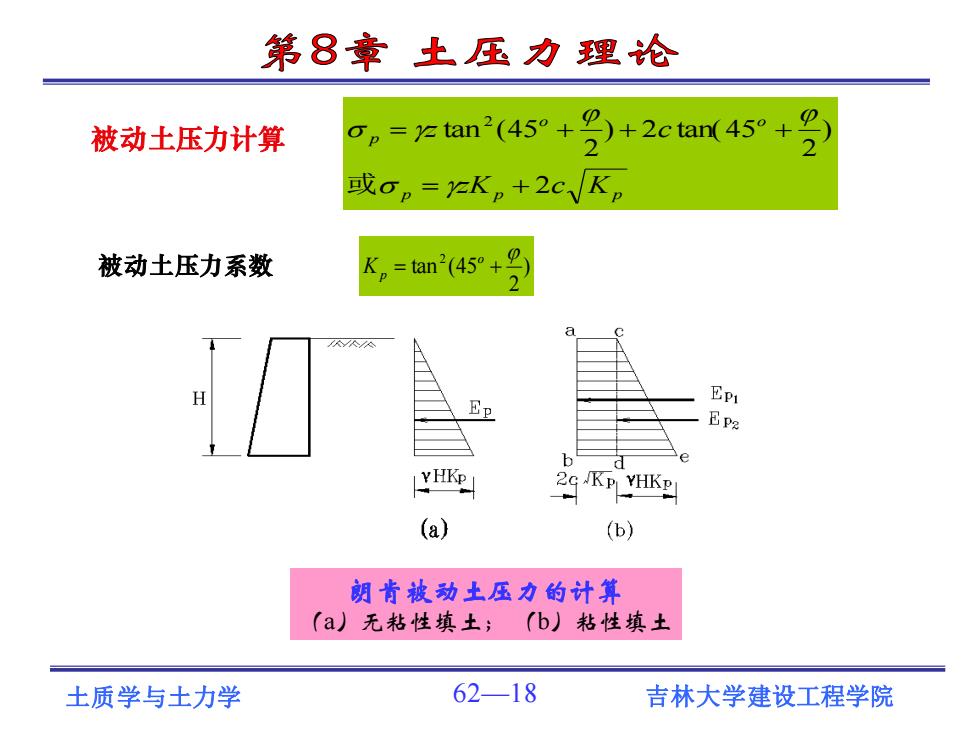
第8章土压力理论 被动土压力计算 op=y tan2(45+P)+2ctan(45+ 或op=K。+2c√K 被动土压力系数 K=tan(45°+ 9 Epy EP2 b 2G KP YHKP (a) (b) 朗肯被动土压力的计算 (a)无粘性填土;(b)粘性填土 土质学与土力学 62-18 吉林大学建设工程学院
土质学与土力学 62—18 吉林大学建设工程学院 被动土压力计算 p p p o o p zK c K z c 2 ) 2 ) 2 tan(45 2 tan (45 2 = + = + + + 或 ) 2 tan (45 2 = + o 被动土压力系数 Kp 朗肯被动土压力的计算 (a)无粘性填土; (b)粘性填土

第8章土压力理论 无粘性土的朗肯被动土压力沿深度呈三角形分布 Ep= 5H2K。 E方向垂直墙背,作用点位于作用点位于墙底以上H3处。 粘性土由于℃的存在增加了被动土压力,故被动土压力呈梯形 E。=HK。+2cHVK, E,方向垂直墙背,作用点位于作用点在梯形的形心上,也可求出。 土质学与土力学 62-19 吉林大学建设工程学院
土质学与土力学 62—19 吉林大学建设工程学院 粘性土由于c的存在增加了被动土压力,故被动土压力呈梯形 无粘性土的朗肯被动土压力沿深度呈三角形分布 Ep方向垂直墙背,作用点位于作用点位于墙底以上H /3处。 Ep H Kp 2 2 1 = p p Kp E H K 2cH 2 1 2 = + Ep方向垂直墙背,作用点位于作用点在梯形的形心上,也可求出

第8章土压力理论 关于朗肯条件的讨论 填土中存在朗肯主动应力状态的条件: ①挡土墙不阻碍第二破裂面的形成,即墙背倾角>夹角 ②位于第二破裂面与墙背之间的土楔CBA不沿墙背下滑,而是附在 墙背上与墙一起移动,即作用在墙背上的总压力与墙背法线的夹角 小于外摩擦角 对粗糙的挡土墙来说,用朗肯理论计算得到的主动土压力偏大, 被动土压力偏小,对于工程是偏于安全的。 土质学与土力学 62-20 吉林大学建设工程学院
土质学与土力学 62—20 吉林大学建设工程学院 关于朗肯条件的讨论 对粗糙的挡土墙来说,用朗肯理论计算得到的主动土压力偏大, 被动土压力偏小,对于工程是偏于安全的。 填土中存在朗肯主动应力状态的条件: ②位于第二破裂面与墙背之间的土楔CBA不沿墙背下滑,而是附在 墙背上与墙一起移动,即作用在墙背上的总压力与墙背法线的夹角 小于外摩擦角 ①挡土墙不阻碍第二破裂面的形成,即墙背倾角>夹角