
仪器分析(含实验) 《仪器分析》课程 第十四章 核磁共振被谱法 Chapter Fourteen Nuclear Magnetic Resonance Spectroscopy For Short:NMR
《仪器分析》课程 仪器分析(含实验) 第十四章 Chapter Fourteen Nuclear Magnetic Resonance Spectroscopy For Short: NMR 核磁共振波谱法

§14.1核磁共振基本原理 一、概述 1.NMR简介 NMR是研究处于磁场中的原子核对射频辐射(Radio-frequency Radiation)的吸收,它是对各种有机和无机物的成分、结构进行 定性分析的最强有力的工具之一,有时亦可进行定量分析。 在强磁场中,原子核发生自旋能级分裂(能级极小:在1.41T磁场中, 磁能级差约为25×10-3J),当吸收外来电磁辐射(109.-1010nm,4- 9O0MHz)时,将发生核自旋能级的跃迁-一产生所谓NMR现象。 sg■■8gg8g88gga■■8g888ggg■■88888g0g8gs8■SsaMEen8■■8s8ggg08gg88888888gggg■■■8888gg8g88想888 SEMsnEn■■8g88g 射频辐射→原子核(强磁场下能级分裂)→吸收→能级跃迁→NMR: 测定有机化合物的结构,HNMR-氢原子的位置、环境以 及官能团和C骨架上的H原子相对数目) 与UV-Vis和红外光谱法类似,NMR也属于吸收光谱,只是研究 的对象是处于强磁场中的原子核自旋能级对射频辐射的吸收。 2.发展历史 1924年:Pauli预言了NMR的基本理论,即:有些核同时具 有自旋和磁量子数,这些核在磁场中会发生分裂;
§14.1 核磁共振基本原理 1. NMR简介 ❖ 与UV-Vis和红外光谱法类似,NMR也属于吸收光谱,只是研究 的对象是处于强磁场中的原子核自旋能级对射频辐射的吸收。 ❖ NMR是研究处于磁场中的原子核对射频辐射(Radio-frequency Radiation)的吸收,它是对各种有机和无机物的成分、结构进行 定性分析的最强有力的工具之一,有时亦可进行定量分析。 ❖ 在强磁场中,原子核发生自旋能级分裂(能级极小:在1.41T磁场中, 磁能级差约为2510-3J),当吸收外来电磁辐射(109 -1010nm, 4- 900MHz)时,将发生核自旋能级的跃迁-产生所谓NMR现象。 射频辐射→原子核(强磁场下能级分裂) →吸收→能级跃迁→NMR 一、概述 测定有机化合物的结构,1H NMR─氢原子的位置、环境以 及官能团和C骨架上的H原子相对数目) 2. 发展历史 1924年:Pauli 预言了NMR的基本理论,即:有些核同时具 有自旋和磁量子数,这些核在磁场中会发生分裂;
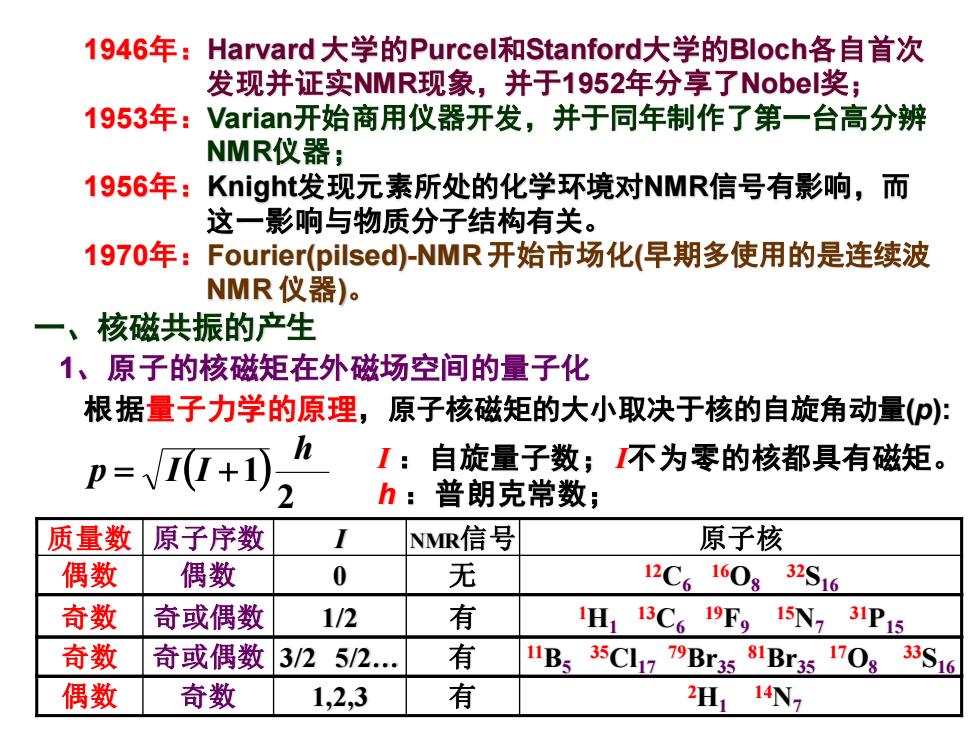
1946年:Harvard大学的Purcel和Stanford:大学的Bloch各自首次 发现并证实NMR现象,并于1952年分享了Nobel奖; 1953年:Varian:开始商用仪器开发,并于同年制作了第一台高分辨 NMR仪器; 1956年:Knight发现元素所处的化学环境对NMR信号有影响,而 这一影响与物质分子结构有关。 1970年:Fourier(pilsed)-NMR开始市场化(早期多使用的是连续波 NMR仪器)。 核磁共振的产生 1、原子的核磁矩在外磁场空间的量子化 根据量子力学的原理,原子核磁矩的大小取决于核的自旋角动量()小: h 1:自旋量子数;不为零的核都具有磁矩。 h:普朗克常数; 质量数原子序数 I NvMR信号 原子核 偶数 偶数 0 无 12C6160g 32S6 奇数 奇或偶数 1/2 有 H113C619Fg 15N73P15 奇数 奇或偶数3/25/2. 有 1B535Cl1779Br3581Br35170g 33S16 偶数 奇数 1,2,3 有 2H114N7
一、核磁共振的产生 1、原子的核磁矩在外磁场空间的量子化 ( ) 2 1 h p = I I + I :自旋量子数; I不为零的核都具有磁矩。 h :普朗克常数; 质量数 原子序数 I NMR信号 原子核 偶数 偶数 0 无 12C6 16O8 32S16 奇数 奇或偶数 1/2 有 1H1 13C6 19F9 15N7 31P15 奇数 奇或偶数 3/2 5/2. 有 11B5 35Cl17 79Br35 81Br35 17O8 33S16 偶数 奇数 1,2,3 有 2H1 14N7 根据量子力学的原理,原子核磁矩的大小取决于核的自旋角动量(p): 1946年:Harvard 大学的Purcel和Stanford大学的Bloch各自首次 发现并证实NMR现象,并于1952年分享了Nobel奖; 1953年:Varian开始商用仪器开发,并于同年制作了第一台高分辨 NMR仪器; 1956年:Knight发现元素所处的化学环境对NMR信号有影响,而 这一影响与物质分子结构有关。 1970年:Fourier(pilsed)-NMR 开始市场化(早期多使用的是连续波 NMR 仪器)

具有自旋角动量p)的核在自旋式会产生核磁矩(: u=y P y为磁旋比,不同的核有不同的磁旋比。 当将自旋核置于外加磁场H。中时,根据量子 力学原理,由于磁矩与磁场相互作用。磁矩相对 于外加磁场有不同的取向,它们在外磁场方向的 投影是量子化的,可以用磁量子数(m)描述: m=l,-1,-2,.-1 2=1个取向 右手定则 对于具有1,的核量子化能级的能量为: Ho:外加磁场强度(G-高斯); E=- -BHo B:核磁子(5.049×10-31J.G1); u:以为单位的磁旋比
具有自旋角动量(p)的核在自旋式会产生核磁矩(μ) : μ=γ P 右手定则 γ 为磁旋比,不同的核有不同的磁旋比。 当将自旋核置于外加磁场H0中时,根据量子 力学原理,由于磁矩与磁场相互作用。磁矩相对 于外加磁场有不同的取向,它们在外磁场方向的 投影是量子化的,可以用磁量子数(m)描述: μ 对于具有I、m的核量子化能级的能量为: H0 I m E = − H0:外加磁场强度(G-高斯); β:核磁子(5.049×10-31J.G-1 ); μ:以β为单位的磁旋比. m=I , I-1 ,I-2,.-I 2I=1个取向
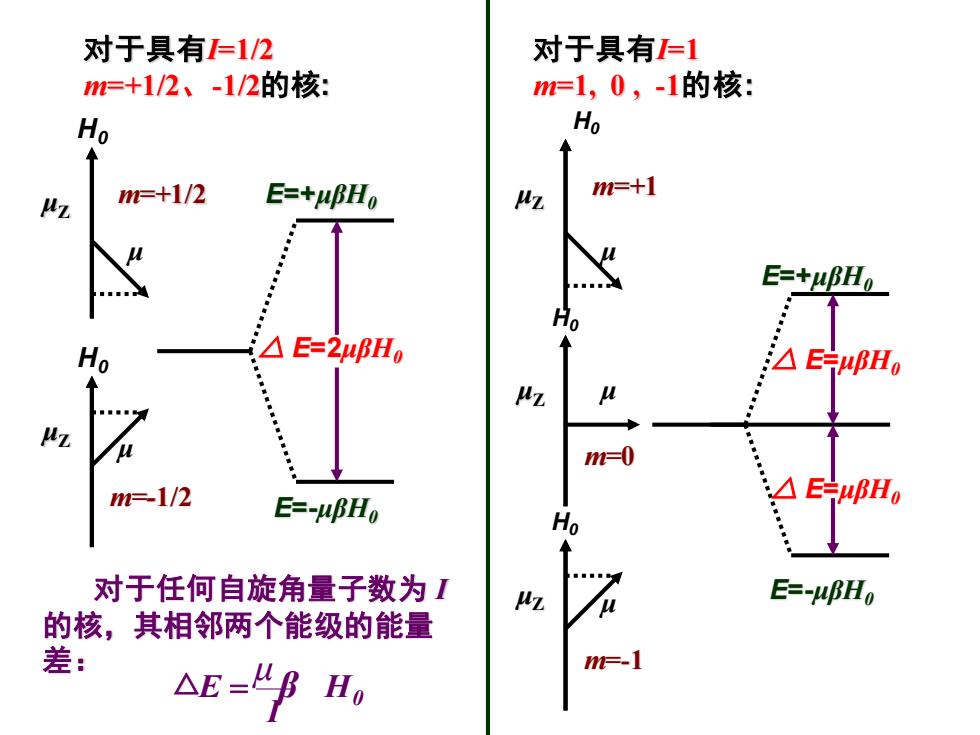
对于具有=1/2 对于具有=1 m=+1/2、-1/2的核: m=1,0,-1的核: Ho Ho m=+1 z m=+1/2 E=+uBHo MZ E=+uBHo Ho i△E=2H0 △EHG = m=1/2 △EHo E=-uBHo 对于任何自旋角量子数为 E=-uBHo 的核,其相邻两个能级的能量 差: △E= Ho
对于具有I=1/2 m=+1/2、-1/2的核: 对于具有I=1 m=1, 0 , -1的核: μZ m=0 H0 μ μZ m=+1/2 H0 μ μZ m=-1/2 H0 μ μZ m=+1 H0 μ μZ m=-1 H0 μ E=-μβH0 E=+μβH0 △ E=2μβH0 E=-μβH0 E=+μβH0 △ E=μβH0 △ E=μβH0 对于任何自旋角量子数为 I 的核,其相邻两个能级的能量 差: H0 I E = μ △ β