中国科学技术大学：《计算机视觉》课程教学资源（PPT课件讲稿）第三章 图像处理基础（1/2）

图像形式 ■2维灰度图像 ■ 3维密度图像 湖 2.5维距离图像

图像形式 § 2维灰度图像 § 3维密度图像 § 2.5维距离图像

与祥 麻

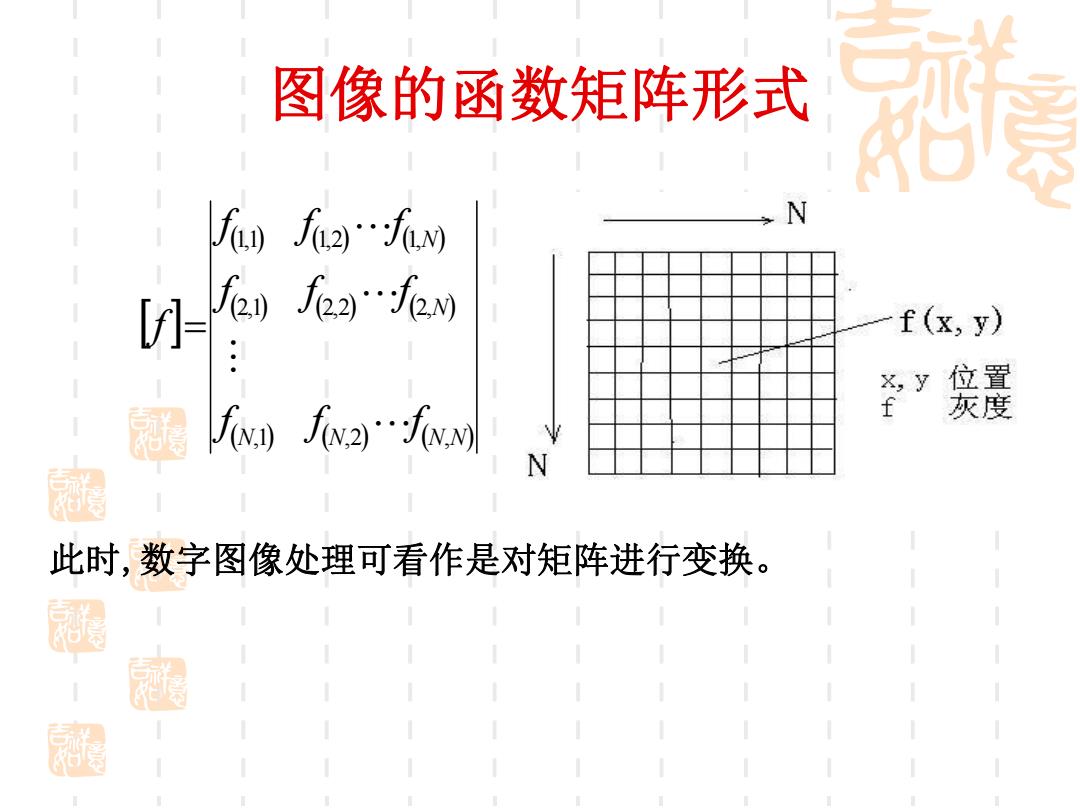
图像的函数矩阵形式 ff2…fiw Jen Je""e f(x,y) X,y 位置 不)无2不 灰度 N 此时，数字图像处理可看作是对矩阵进行变换。 湖

              N  N  N N N N f f f f f f f f f f ,1 ,2 , 2,1 2,2 2, 1,1 1,2 1,      此时,数字图像处理可看作是对矩阵进行变换。 图像的函数矩阵形式

图像也可以由向量来表示： 二维图像矩阵 fao Jz"faw NXN象素 门-侧流 fio fx"Jm f(2,1) 矩阵和矢量间关系： 表示成矢量 形式为： f(N,) 涵 f0,2) f-Σ[A]f]7。 n=] 矢量 f= 秋私 f(N,2) [f]=∑[A]'f n三 fa.N (n=k时提取第k 列理解) f (N .N

图像也可以由向量来表示： 二维图像矩阵 N×N象素               N  N  N N N N f f f f f f f f f f ,1 ,2 , 2,1 2,2 2, 1,1 1,2 1,      表示成矢量 形式为：              N N  N N N f f f f f f f f , 1 , , 2 1 , 2 ,1 2 ,1 1 ,1     矢量              N n n n N n n n f A f V f A f V 1 1 1 1 矩阵和矢量间关系： （n=k时提取第k 列理解）

图像的几何函数形式（流形 45 60 98 127 132 133 137 133 45 6的 93 123 126 128 131 133 47 65 96 115 119 123 135 137 47 63 91 107 113 122 133 134 50 59 80 97 110 123 133 134 49 53 68 83 97 113 128 133 50 50 58 70 84 102 16 126 50 50 52 58 6的 86 101 120 吉 履

图像的几何函数形式（流形）