
第二章量子力学基础 MTSD@UPC 第一节量子力学起源及相关实验事实 黑体辐射 例:298K时,比较某辐射体(如暖气片或白炽灯)在450nm(蓝光)和700 nm(红光)的能量输出。 解:可利用Planck分布来求算, p(,T) 入2 ehc/AaknT-1 e(A2,T) ehe/AikaT1 he (6.626×10-34Js)×(2.998×10°ms1) Xk7-(450×109m)×(1.381X1023JK)×(298K) =107.2. hc (6.626×1034Js)×(2.998×108ms1) T=(700×109m)×1.381×1023JK1)×(298K) =68.9. 故有: P(Ai,T) e68.9-1 p(2,T) 700X109m×。m.2-7 (450×109nm) =9.11×(2.30×1027)=2.10×1016 练习:太阳中心温度约为13.6MK,试比较此温度下蓝光和红光的能量输出。 2022/3/24 材料化学系:结构化学 11
MTSD@UPC 2022/3/24 材料化学系:结构化学 11 第二章 量子力学基础 第一节 量子力学起源及相关实验事实 黑体辐射 练习:太阳中心温度约为13.6 MK,试比较此温度下蓝光和红光的能量输出。 例:298K时,比较某辐射体(如暖气片或白炽灯)在450 nm(蓝光)和700 nm (红光)的能量输出。 解:可利用Planck分布来求算, 故有:

第二章量子力学基础 MTSD@UPC 第一节量子力学起源及相关实验事实 黑体辐射 ·Planck分布的物理意义 ·Planck分布能够解释已有实验结果,并能够预测实验 现象 ·黑体辐射中,辐射的电磁波由黑体表面原子的热运动 激发: ·经典力学:所有振子共享黑体提供的能量(能量均分原理) →高频振子也可以被激发→紫外灾难 ·普朗克量子假设:只有当黑体提供的能量超过v时才能激发 电磁振子→无足够能量激发高频振子→高频振子不能被激 发 量子化的效果:降低了高频振子被激发的可能性,从而降低了高频辐 射对能量密度的贡献→解决紫外灾难 2022/3/24 材料化学系:结构化学 12
MTSD@UPC • Planck分布的物理意义 • Planck分布能够解释已有实验结果,并能够预测实验 现象 • 黑体辐射中,辐射的电磁波由黑体表面原子的热运动 激发: • 经典力学:所有振子共享黑体提供的能量(能量均分原理) ➔ 高频振子也可以被激发 ➔ 紫外灾难 • 普朗克量子假设:只有当黑体提供的能量超过ℎ𝜈时才能激发 电磁振子 ➔ 无足够能量激发高频振子 ➔ 高频振子不能被激 发 2022/3/24 材料化学系:结构化学 12 第二章 量子力学基础 第一节 量子力学起源及相关实验事实 黑体辐射 量子化的效果:降低了高频振子被激发的可能性,从而降低了高频辐 射对能量密度的贡献➔ 解决紫外灾难

第二章量子力学基础 MTSD@UPC 第一节量子力学起源及相关实验事实 固体比热容 ·Dulong-Peit定律 ·19世纪早期,基于少量实验 Cv= aU OTv 25J K-1 mol-1 ·易用经典物理解释 ·原子在平衡位置附近振动 ·能量均分原理→每个自由度贡献kBT ·三维空间→三个自由度 U=3NAkT=3RT Cv= aU ∂Tv =3R ·然而,并不准确。。。(后来有了NB的制冷技术) 2022/3/24 材料化学系:结构化学 13
MTSD@UPC • Dulong-Petit 定律 • 19世纪早期,基于少量实验 • 易用经典物理解释 • 原子在平衡位置附近振动 • 能量均分原理➔每个自由度贡献𝑘𝐵𝑇 • 三维空间 ➔ 三个自由度 • 然而,并不准确。。。(后来有了NB的制冷技术) 2022/3/24 材料化学系:结构化学 13 第二章 量子力学基础 第一节 量子力学起源及相关实验事实 固体比热容
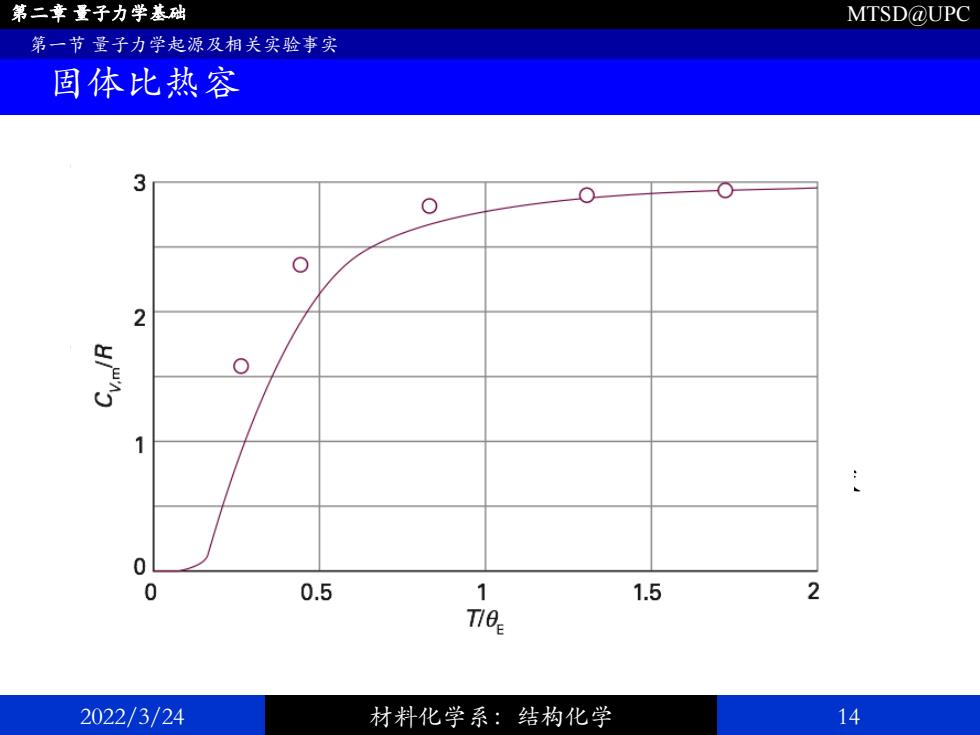
第二章量子力学基础 MTSD@UPC 第一节量子力学起源及相关实验事实 固体比热容 3 0 2 0 0 0.5 1 1.5 2 Tie 2022/3/24 材料化学系:结构化学 14
MTSD@UPC • Dulong-Petit 定律的局限: • 随制冷技术的发展,低温下测量热容成为可能 • 单原子固体的比热容在低温下低于3R • 𝑇 → 0时,𝐶𝑉 → 0 • Einstein公式: • 1905,每个原子以频率𝜈振动 • 采用Planck的假设,振子能量只能为ℎ𝜈的整数倍 • 抛弃能量均分原理,计算原子振动对比热容的贡献 • Einstein 温度:𝜃𝐸 = ℎ𝜈/𝑘𝐵 2022/3/24 材料化学系:结构化学 14 第二章 量子力学基础 第一节 量子力学起源及相关实验事实 固体比热容
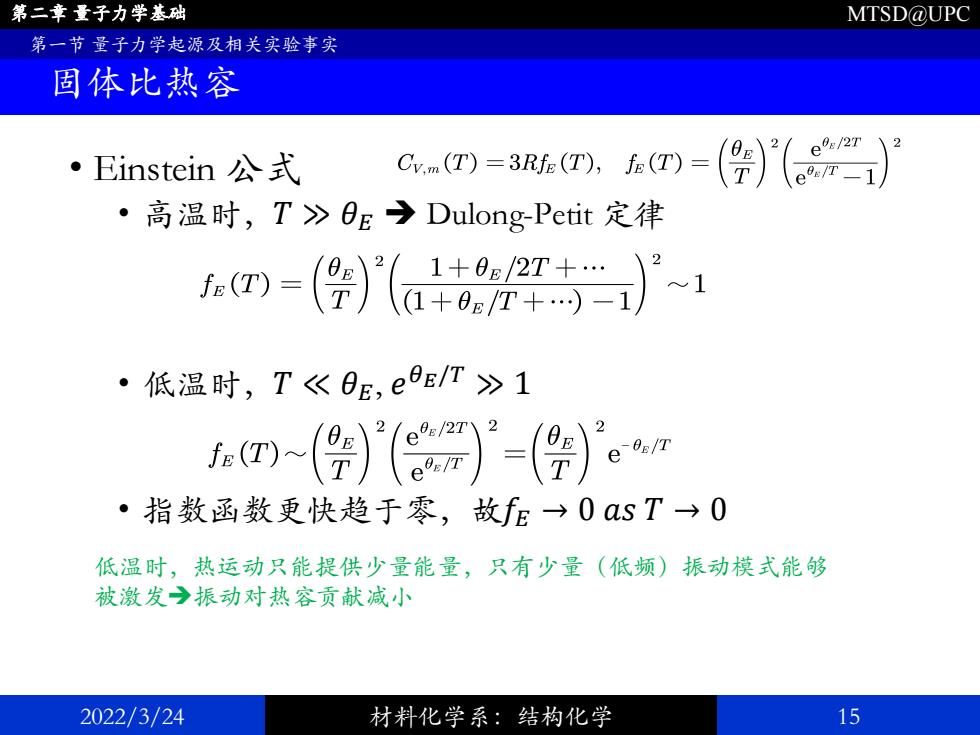
第二章量子力学基础 MTSD@UPC 第一节量子力学起源及相关实验事实 固体比热容 e/27 ·Einstein公式 cm=3a.=(=)'() ·高温时,T>BE→Dulong-Petit定律 四-(){a=1 ·低温时,T《0E,e8E/T>1 e-oe/T ·指数函数更快趋于零,故fE→0aST→0 低温时,热运动只能提供少量能量,只有少量(低频)振动模式能够 被激发振动对热容贡献减小 2022/3/24 材料化学系:结构化学 15
MTSD@UPC • Einstein 公式 • 高温时,𝑇 ≫ 𝜃𝐸 ➔ Dulong-Petit 定律 • 低温时,𝑇 ≪ 𝜃𝐸, 𝑒 𝜃𝐸/𝑇 ≫ 1 • 指数函数更快趋于零,故𝑓𝐸 → 0 𝑎𝑠 𝑇 → 0 2022/3/24 材料化学系:结构化学 15 第二章 量子力学基础 第一节 量子力学起源及相关实验事实 固体比热容 低温时,热运动只能提供少量能量,只有少量(低频)振动模式能够 被激发➔振动对热容贡献减小