
Chapter3群的类分解 1.共轭类 共轭:设f、h是群G的两个元素,若有元素g∈G,使得 8=h,则称元素h与f共轭。记为h~f 共轭具有传递性: 若~h,f方~h,则f~f2 证明: f-g.hg f=g2hg2 f=81(g2f382)81-(882f5(g82) 类:群G中所有互为共轭的元素集合组成一个类。 记:K(A)={8,g'}g,跑遍所有的群元素
Chapter 3 群的类分解 -1 gfg = , h h f 1 2 f f 1 -1 -1 1 1 2 22 -1 -1 -1 -1 -1 1 1 2 22 1 12 2 12 = = = ( ) =( ) ( ) f g hg f g hg f g g fg g gg f gg 1. 共轭类 共轭:设f、h是群 G 的两个元素,若有元素 使得 则称元素 h 与 f 共轭。记为 共轭具有传递性: 若 则 证明: 类:群 G 中所有互为共轭的元素集合组成一个类。 记: gi 跑遍所有的群元素。 -1 ( ) { } K A i i g ag g G , 1 2 f h, , f h
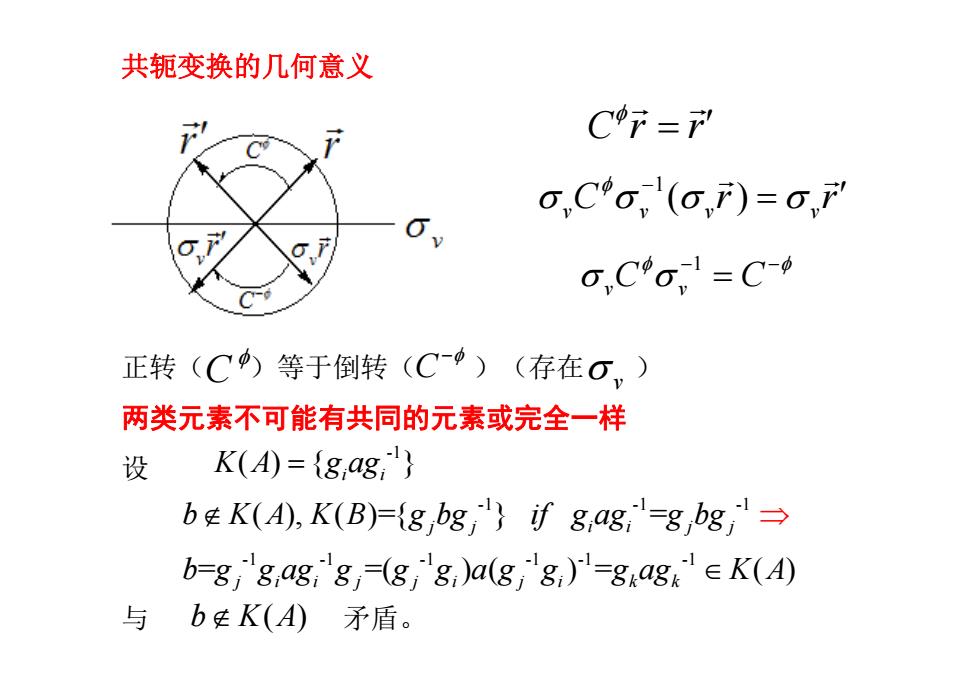
共轭变换的几何意义 C行= o,Co,(o,)=0,F O,Cσ,1=C-4 正转(C)等于倒转(C$)(存在O,) 两类元素不可能有共同的元素或完全一样 设 K(A)={8,ag,} bK(A),K(B)=(g bgi if gag;-g bg b=8,8,g,g,-(g,g,)a(g,g)'=84agk∈K(A) 与b庄K(A)矛盾
共轭变换的几何意义 正转( )等于倒转( )(存在 ) 两类元素不可能有共同的元素或完全一样 设 与 矛盾。 Cr r 1( ) v vv v C rr 1 v v C C C C v -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 ( ) { } ( ), ( )={ } = = =( ) ( ) = ( ) i i j j ii j j jii j ji ji kk K A g ag b K A K B g bg if g ag g bg b g g ag g g g a g g g ag K A b KA ( )

据此,可将群进行类分解: G={80,81,,8m-1} K(E)=(8,e g)=e Ko(E) K(A) K (4) bEK(A)→K(B)={8,bg,} K,(B) G=UK, 例子:C3m E.C.C.a.o..o." 类:{E} {C,C} {o,o,”,o,} 交换群群元素自成一类 8,ag,=88,a=a8∈G
0 1 -1 -1 0 1 -1 2 { , , ..., } ( ) { } ( ) ( ) ( ) ( ) ( ) { } ( ) n i i i i i G gg g K E geg e K E K A KA b K A K B gbg K B G K 2 3 33 , , , , , C EC C v vv v 2 3 3 , , , E CC vv v -1 -1 = = i i ii i g ag g g a a g G 据此,可将群进行类分解: 例子: 类: 交换群群元素自成一类
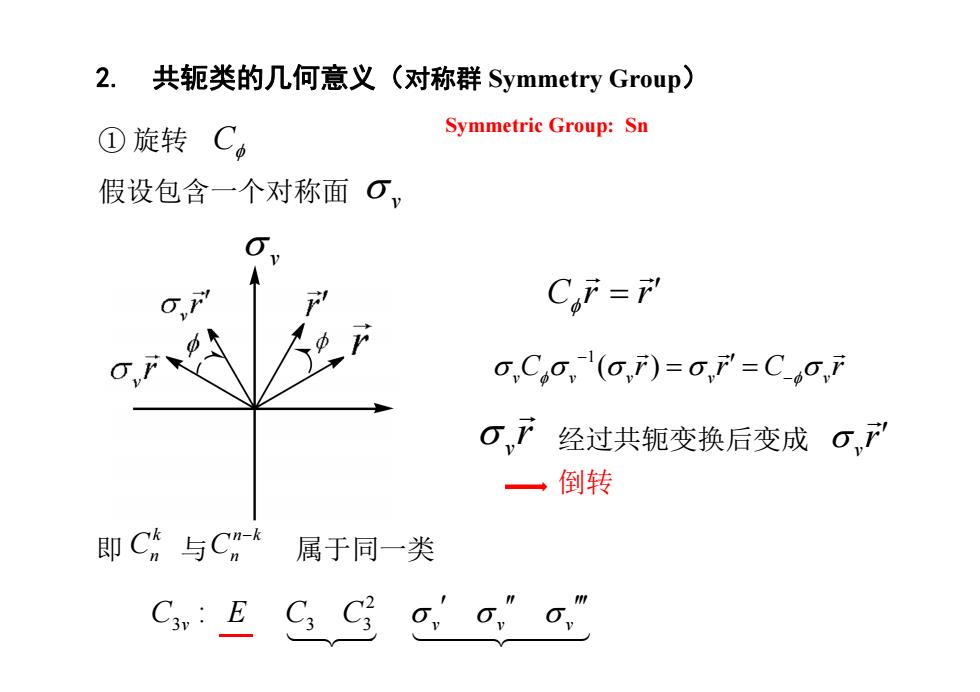
2.共轭类的几何意义(对称群Symmetry Group) ①旋转 C。 Symmetric Group:Sn 假设包含一个对称面可, CF=F 0C0,(o)=0,'=C0,f O,下经过共轭变换后变成σ” 一倒转 即C与CW 属于同一类 Ca:E C:Ci,"o
2. 共轭类的几何意义(对称群 Symmetry Group ) ① 旋转 假设包含一个对称面 C v Cr r 1( ) vvv v v C r rC r v r 经过共轭变换后变成 v r 即 与 属于同一类 k Cn n k Cn 2 3 33 : C ECC v vv v Symmetric Group: Sn v 倒转

如存在一个垂直C。的面O oCo6=C。 o[xy,]=[x,y,-] C6[x,y,]=[x,y,z] a,C.[x.y.=]=[x.y,-=] Co[xy,]=[x,y,-] →C606=0C6 ②对称面 i>OCn=COn 0h自成一类
C h 1 = ,, ,, ,, , , ,, , , ,, , , h h h h h h h C C xyz xy z C xyz x y z C xyz x y z C xyz x y z C C hn nh C C 如存在一个垂直 的面 ② 对称面 ⅰ> h 自成一类