
因为各处理重复数不等,必须先计算出平均重复 次数no 2 25-62+62+52+42+42 25 4.96 于是,标准误: Sx=VMe/n0=V1.94/4.96=0.625 上一张下一张主页退出
于是,标准误: 4.96 25 6 6 5 4 4 25 5 1 1 1 1 2 2 2 2 2 2 0 = + + + + − − = − − = i i i n n n k n Sx = MSe / n0 = 1.94 / 4.96 = 0.625 上一张 下一张 主 页 退 出 因为各处理重复数不等,必须先计算出平均重复 次数n0:
字母标记表示结果 处理 均值 5%显著水平 1%极显著水平 处理1 20.2 a A 处理4 19.6 a AB 处理3 18.3 ab ABC 处理2 17.2 处理5 16.6 QO BC
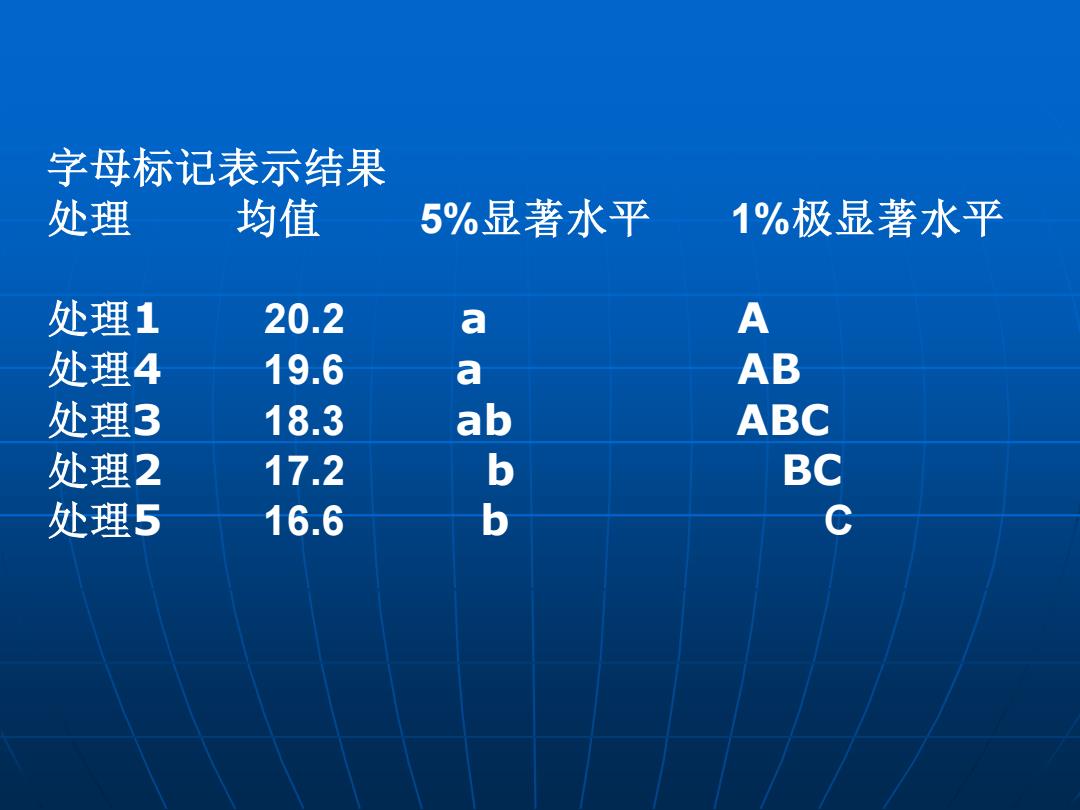
字母标记表示结果 处理 均值 5%显著水平 1%极显著水平 处理1 20.2 a A 处理4 19.6 a AB 处理3 18.3 ab ABC 处理2 17.2 b BC 处理5 16.6 b C

根据dfe=20,秩次距k=2,3,4,5,从附表 6中查出a=0.05与a=0.01的临界SSR值,乘以 0.625,即得各最小显极差,所得结果列于表6-19。 表6-19 SSR值及LSR值表 秩次距( SSRao SSRao LSRaos LSRaoP 20 2.95r 4.02 1.844 2.513 3和 3.10 4.22 1.938+ 2.638+ 20 4 3.18 4.33 1.988+ 2.706 5 3.25 4.40 2.031 2.750 上一张下一张主页退出
根据dfe=20,秩次距k=2,3,4,5,从附表 6中查出α=0.05与α=0.01的临界SSR值,乘以 0.625,即得各最小显极差,所得结果列于表6-19。 上一张 下一张 主 页 退 出 表6-19 SSR值及LSR值表

将表6-18中的各个差数与表6-19中相应的最小 显著极差比较,作出推断。检验结果已标记在表6-18 中。 多重比较结果表明 大B1、B4品种的平均增重极显著或显著高于B2、B5品 种的平均增重,其余不同品种之间差异不显著 。 大可以认为B1、B4品种增重最快,B2、B5品种增重较 差,B3品种居中
将表6-18中的各个差数与表6-19中相应的最小 显著极差比较,作出推断。检验结果已标记在表6-18 中。 多重比较结果表明: ★B1、B4品种的平均增重极显著或显著高于B2、B5品 种的平均增重,其余不同品种之间差异不显著。 ★可以认为B1、B4品种增重最快,B2、B5品种增重较 差,B3品种居中

两因素的试验资料的方差分析 一、交叉分组资料的方差分析 1、无重复的 P118 2、有重复的 P125 二、系统分组资料的方差分析 1、次级样本含量相等 P135 2、次级样本含量不等 P138
两因素的试验资料的方差分析 ◼ 一、交叉分组资料的方差分析 1、无重复的 P118 2、有重复的 P125 ◼ 二、系统分组资料的方差分析 1、次级样本含量相等 P135 2、次级样本含量不等 P138