
二、各处理重复数不等的方差分析 设处理数为k; 各处理重复数为n1,n2,,nk: 试验观测值总数为N=∑n,。则 C=x2/N SS,=∑∑x号-C df,=N-1 SS,=∑x/n,-C df,=k-1 SS。=SS7-SS, c。=dfr-f 上一张下一张主页退出
二、各处理重复数不等的方差分析 设处理数为k;各处理重复数为n1,n2,…,nk; 试验观测值总数为 。则 C x / N 2 .. = 上一张 下一张 主 页 退 出 SSt =xi / ni −C 2 . SST =xij −C 2 SSe = SST − SSt dfT = N −1 df = k −1 t dfe = dfT − dft N =ni
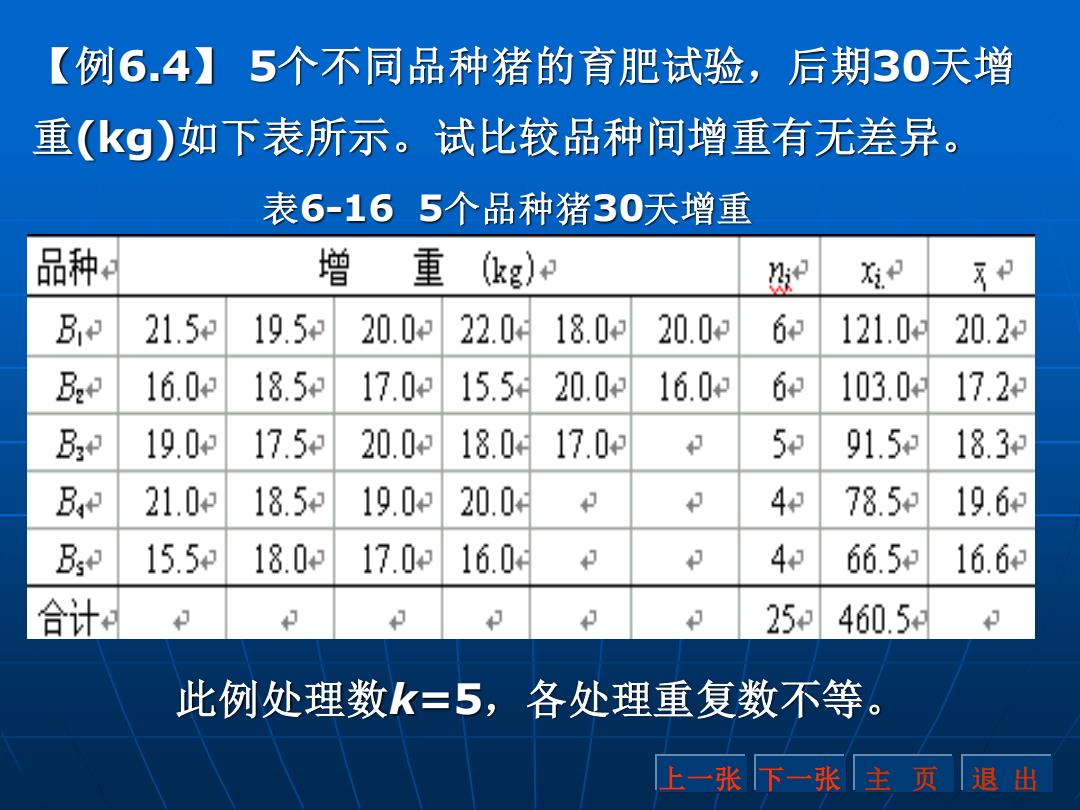
【例6.4】5个不同品种猪的育肥试验,后期30天增 重(kg)如下表所示。试比较品种间增重有无差异。 表6-165个品种猪30天增重 品种e 增重 (kg)e 数 x B 21.5 19.5 20.0 22.0 18.0 20.0 6和 121.0 20.2 Bre 16.0 18.5 17.0 15.5 20.0 16.0 6和 103.0 17.2 Bae 19.0 17.5 20.0 18.0 17.0 5 91.5 18.3 Be 21.0 18.5 19.0 20.0 4 78.5 19.6 Bye 15.5 18.0 17.0 16.0 4 66.5 16.6 合计 25460.5 此例处理数k=5,各处理重复数不等。 上一张下一张主页退出
【例6.4】 5个不同品种猪的育肥试验,后期30天增 重(kg)如下表所示。试比较品种间增重有无差异。 表6-16 5个品种猪30天增重 上一张 下一张 主 页 退 出 此例处理数k=5,各处理重复数不等

1、计算各项平方和与自由度 C=x2/N=460.52/25=8482.41 SS7=∑∑x7-C=(21.52+19.52+…+17.02+16.02)-8482.41 =8567.75-8482.41=85.34 SS,=∑x/n,C (121.02/6+103.02/6+91.52/5+78.82/4+66.52/4)-C 8528.91-8482.41=46.50 SS。=SS7-SS,=85.34-46.50=38.84 d=N-1=25-1=24 df=k-1=5-1=4 df。=d-d5=24-4=20 上一张下一张主页退出
1、计算各项平方和与自由度 / 460.5 / 25 8482.41 2 2 C = x.. N = = 上一张 下一张 主 页 退 出 8567.75 8482.41 85.34 (21.5 19.5 17.0 16.0 ) 8482.41 2 2 2 2 2 = − = SST =xi j −C = + ++ + − 8528.91 8482.41 46.50 (121.0 / 6 103.0 / 6 91.5 / 5 78.8 / 4 66.5 / 4) / 2 2 2 2 2 2 . = − = = + + + + − = − C SSt xi ni C SSe = SST − SSt = 85.34− 46.50 = 38.84 df = N −1= 25−1= 24 T df = k −1= 5−1= 4 t = − = 24− 4 = 20 e T t df df df
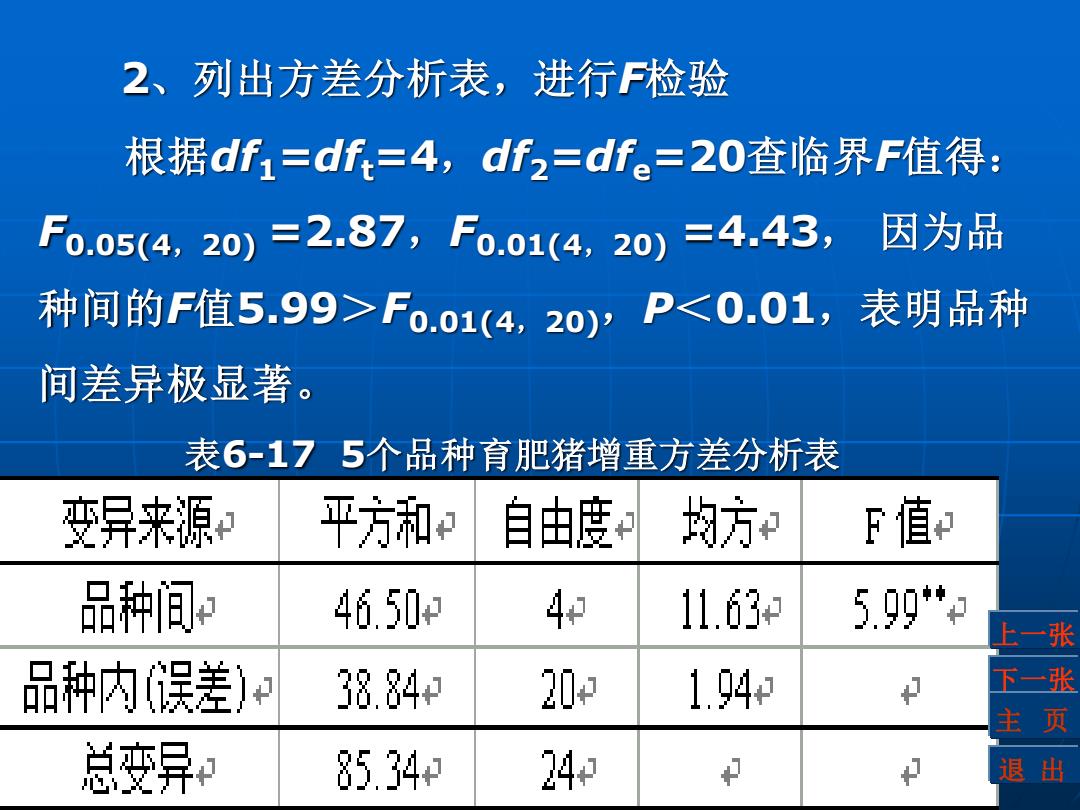
2、列出方差分析表,进行F检验 根据df1=df=4,df2=dfe=20查临界F值得: F0.05(4,20)=2.87,F0.01(4,20)=4.43, 因为品 种间的F值5.99>F0.o1(4,20yP<0.01,表明品种 间差异极显著。 表6-175个品种育肥猪增重方差分析表 变异来源 平方和 自由度利 均方和 F值 品种间 46.50 4 11.63 5.99* 张 品种内误差) 38.84+ 20 1.94 下一张 主页 总变异+ 85.34+ 24 中 退出
2、列出方差分析表,进行F检验 根据df1=dft=4,df2=dfe=20查临界F值得: F0.05(4,20) =2.87,F0.01(4,20) =4.43, 因为品 种间的F值5.99>F0.01(4,20),P<0.01,表明品种 间差异极显著。 下一张 主 页 退 出 上一张 表6-17 5个品种育肥猪增重方差分析表
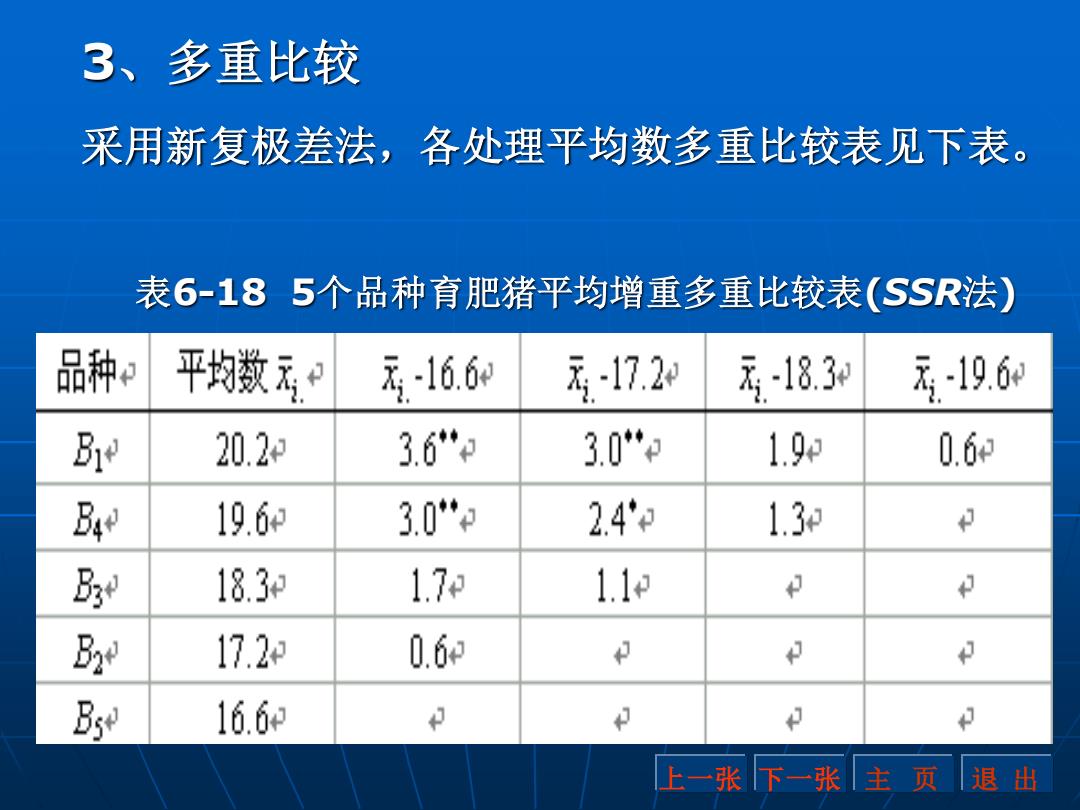
3、多重比较 采用新复极差法,各处理平均数多重比较表见下表。 表6-185个品种育肥猪平均增重多重比较表(SSR法) 品种e 平均数无P 元-16.6 元-17.2 元1830 元19.60 Bre 20.2 3.6" 3.0" 1.9p 0.6 Bd 19.6 3.0" 2.4 1.3 B 183 1.7 1.1 B 17.2 0.6 Bse 16.6 上一张下一张主页退出
表6-18 5个品种育肥猪平均增重多重比较表(SSR法) 上一张 下一张 主 页 退 出 3、多重比较 采用新复极差法,各处理平均数多重比较表见下表