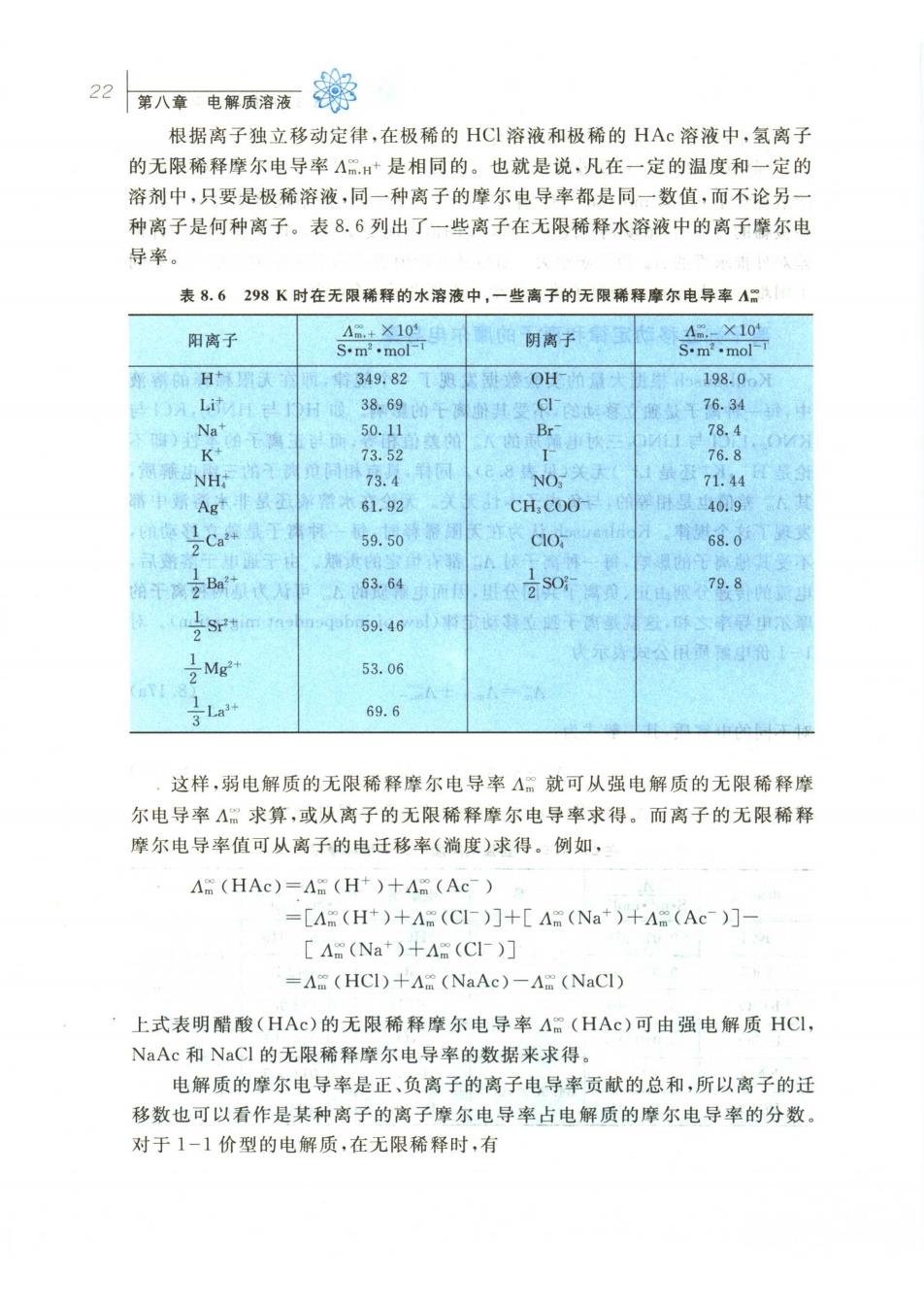
22 男八章电界质洛清黎 根据离子独立移动定律,在极稀的HC溶液和极稀的HAc溶液中,氢离子 的无限稀释摩尔电导率△m+是相同的。也就是说,凡在一定的温度和一定的 溶剂中,只要是极稀溶液,同一种离子的摩尔电导率都是同一数值,而不论另 种离子是何种离子。表8.6列出了一些离子在无限稀释水溶液中的离子摩尔电 导率。 表8.6298K时在无限稀释的水溶液中,一些离子的无限稀释摩尔电导率A 阳离子 阴离子宝 H州灵 349.82 OH 5198.06月 38,690 76.34 Br- 78,4 K 73.52 1 NH时 1同73.4 NO 76.8 71.44 中Ag 61.92 CH.COO- 时显40.9 59.50 68.0 Ba 63.64 79.8 pb59.46 53.06 69.6 这样,弱电解质的无限稀释摩尔电导率△:就可从强电解质的无限稀释摩 尔电导率A。求算,或从离子的无限稀释摩尔电导率求得。而离子的无限稀释 摩尔电导率值可从离子的电迁移率(淌度)求得。例如, A (HAc)=A (H+)+A (Ac-) =[A (H)+A (CI-)]+A (Na*)+A (Ac-)]- A (Na+)+A (C)] =A (HCI)+A (NaAc)-A (NaCI) 上式表明醋酸(HAc)的无限稀释摩尔电导率A(HAc)可由强电解质HCI, NaAc和NaCI的无限稀释摩尔电导率的数据来求得。 电解质的摩尔电导率是正、负离子的离子电导率贡献的总和,所以离子的迁 移数也可以看作是某种离子的离子摩尔电导率占电解质的摩尔电导率的分数 对于1-1价型的电解质,在无限稀释时,有

众583电解质溶液的电号23 4m=4m.+十Am.- (8.18) 对于浓度不太大的强电解质溶液,设它完全解离,可近似有 Am=4m.+十Am. 4= t=4 Am (8.19) t+,t-和A的值都可以由实验测得,从而就可以计算离子的摩尔电导率 离子的摩尔电导率可由离子的电迁移率求得。设图8.6的实验中电场是均 匀的,则5在数值上等于号又因为=:=u号,故式(85)可写成 I=caA(u十u-)号F (8.20) 已知 e=G片-名片 将式(8.20)代入上式,并整理得: k=cxaz+(u4十-)F 根据摩尔电导率的定义,这时电解质的浓度为cxz+,所以有 Am一cx2+ =a(u+十u-)F (8.21) 对无限稀释的电解质溶液,a=1,故 A==(年+2)F (8.22) 又因为 4m=Am.+十4m. 所以 Am.+=uTF Am.-=uF (8.23) 对于浓度不太大的强电解质溶液,设它完全解离,可近似有 Am.+=u+F An.-=u-F (8.24) 将式(8.24)与式(8.18)结合,可把t,u,4m+,4m.-和Am几个物理量联系在 起,从而可从实验易测的量来计算实验不易测的量或未知的量。 例题有一电导池,电极的有效面积A为2×10·m,两极片间的距离为 0.10m,电极间充以1-1价型的强电解质MN的水溶液,浓度为30mol·m3 两电极间的电势差E为3V,电流强度1为0.003A。已知正离子M的迁移数 t4=0.4

24第八章电系质帝液静 试求: (1)MN的摩尔电导率: (2)M离子的离子摩尔电导率 (3)M离子在上述电场中的移动速率。 解: 0dm×09A20 =1.67×10Sm'mol+ (2)Am.+=t4m=0.4×1.67×102Sm2mol =6.67×101Sm2mol 96 500 C.mol =2.07×10ms (S=01=合A=C、) 由表8.6可见,在水溶液中,H和OH离子的离子摩尔电导率特别大。在表8.1中,这 两个离子的电迁移率也较其他离子大几倍,这说明水溶液中H和OH离子在电场力的作 用下运动速率特别快。H和OH离子的这种异常现象只在水溶液(或含有O基的溶剂 例如ROH)中显现。 有人认为在水溶液中单个的溶剂化的质子的传导是通过一种质子传递机理即Gohu: 电导机理(格鲁萨斯,Grotthus mechanism),而并不是质子本身从溶液的一端迁向另一端,如 图8.13所示。因为质子可以在水分子间转移,所以随着质子从一个水分子传给另一个水分 子,电流就很快沿着氢键被传导,而水分子的排列形式从()变成(b)。以(b)排列方式的水分 子必须翻转,回复到()的排列状态才能再接受(或释放)质子,故电导率的大小取决于水分子 翻转的速度。 OH离子的摩尔电导率也很大,传导机理与上所述类似,只是质子从H,O分子上转移 到OH离子上,这个过程与OH在反方向的运动等价。 文献表明,也有人认为质子在水中形成了H,O离子(即H,O通过氢键再与三个水分 子结合在一起而形成H,O离子)。 电导测定的一些应用 有关溶液电导数据的应用是很广泛的,此处仅择其重要者略述 1,检验水的纯度 普通蒸馏水的电导率约为1×103S·m1,重蒸馏水(蒸馏水经用KMnO
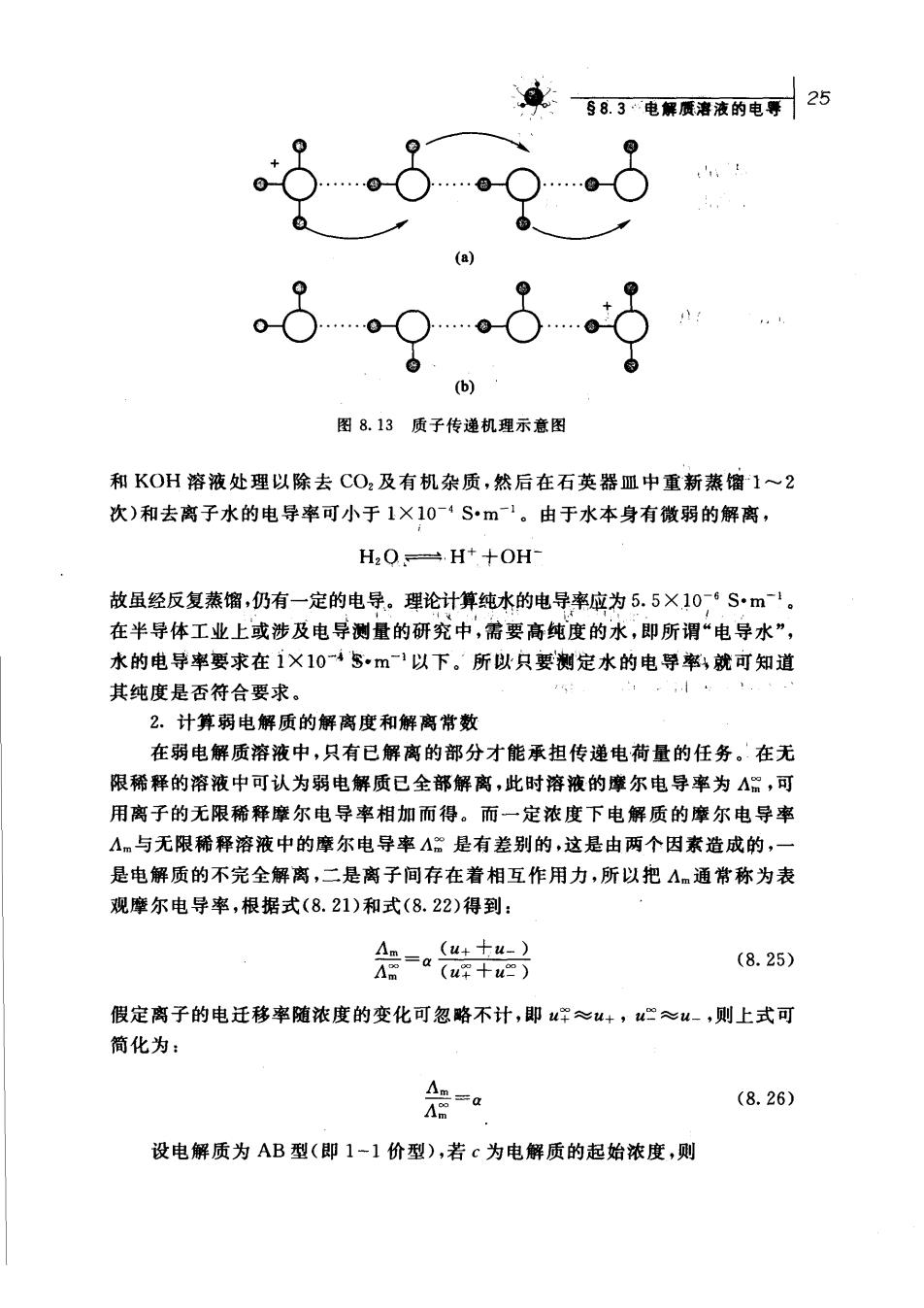
98,3电鼎质液的电导25 .0 (b) 图8.13质子传递机理示意图 和KOH溶液处理以除去CO2及有机杂质,然后在石英器皿中重新蒸馏1~2 次)和去离子水的电导率可小于1×104S•m。由于水本身有微弱的解离, H2O.H+十OH 故虽经反复蒸馏,仍有一定的电导。理论计算纯水的电导率应为5.5×106S·m。 在半导体工业上或涉及电导测量的研究中,需要高纯度的水,即所谓“电导水”, 水的电导率要求在1×104$·m1以下。所以只要测定水的电导率,就可知道 其纯度是否符合要求。 2.计算弱电解质的解离度和解离常数 在弱电解质溶液中,只有已解离的部分才能承担传递电荷量的任务。在无 限稀释的溶液中可认为弱电解质已全部解离,此时溶液的摩尔电导率为△细,可 用离子的无限稀释摩尔电导率相加而得。而一定浓度下电解质的摩尔电导率 A.与无限稀释溶液中的摩尔电导率A是有差别的,这是由两个因素造成的, 是电解质的不完全解离,二是离子间存在着相互作用力,所以把4通常称为表 观摩尔电导率,根据式(8.21)和式(8.22)得到: (8.25) 假定离子的电迁移率随浓度的变化可忽略不计,即学≈u+,u≈u-,则上式可 简化为: 会 (8.26) 设电解质为AB型(即1-1价型),若c为电解质的起始浓度,则

26第入童电界系表夜券 AB→A++B 起始时 0 0 平衡时 c(1-a)ca 将式(8.26)代入后,得 5A品 Am (Am -Am) (8.27) 1 上式也可写作 4.6 (8.28) 以大对A.作图,截距即为左,根据直线的斜率即可求得K”值 这就是Ostwald(奥斯特瓦尔德,1853一1932,俄籍德国物理化学家)的稀释 定律(Ostwald's dilution law)。 例题把浓度为15.81mol·m的酷醋酸溶液注入电导池,已知电导池常数 K是13.7m',此时测得电阻为655。运用表8.6的数值计算醋酸的A, 以及求出在给定条件下醋酸的解离度α和解离常数K。 解: 因为-10-2,0910sm A=兰-20d=132x05mma A■=Am(H+)十Am(Ac) =(349.82+40.9)×10-4Sm2mol =3.91×102Sm2mol =4m=1.32×103Sm2mol a=A2-3.907×10smm0=3.38X10 K2-1-a