
¢58:3电膜质溶液的电导27 15.81molm×(3.38×102)y -1 mol.dm -3.38×10 =1.87×10- Ostwald稀释定律的正确性可以通过实验来验证。表8.7是把稀释定律应 用于HCI和HAc的水溶液所得的数据。 从表8.7可以看出,醋酸的K在浓度不太高时接近于一个常数,但是强电 解质HC的K°值则远不是一个常数。因强电解质的溶液中几乎是全部解离 的,不存在所谓解离度问题,也就不遵守Ostwald稀释定律。 表8.7在298K时根据式(8.27)计算所得的K°值 HCI的水溶液 CH,COOH的水溶液 4m=426.16×10-Sm2mol-1 4=390.72×10-4S.m2.mo1-1 mol.m 4m10 Smmol KX10 mol-m K9X10 0.028408 42513 0.016 0.028014 210.38 1760 0.081181 12A只7 0.02666 015321 11205 1767 0.17743 423.94 0.03355 102821 A只146 1.781 0.31836 423.55 0.05139 2.41400 22917 1.789 0.59146 422.54 0.05995 5.91153 20.962 1.798 0.75404 421 78 0.07169 12.829 14.375 1803 1.5768 105g 50.000 7358 1808 1.8766 419.76 0.1212 52,303 7.202 1.811 3.测定难溶盐的溶解度 一些难溶盐如BSO,(s),AgCI(s)等在水中的溶解度很小,其浓度不能用 普通的滴定方法测定,但可用电导法来求得。以AgC1为例,先测定其饱和溶液 的电导率x(溶液),由于溶液极稀,水的电导率已占一定比例,不能忽略,所以必 需从中减去水的电导率才能得到AgCI的电导率: K(AgCI)=K(溶液)一K(H2O) 摩尔电导率的计算公式为 AAC)Ag器 由于难溶盐的溶解度很小,溶液极稀,所以可以认为Am≈A■,而A。的值可由 离子无限稀释摩尔电导率相加而得,因此可根据上式求得难溶盐的饱和溶液浓 度c(单位是mol·m),要注意所取粒子的基本单元在A.和c中应一致。例如 BaS0,可取A(BaS0,)和c(BaS0,),或A.(2BaS0,)和c号BaS0,),从而可

29第入章电帮浩素繁 计算难溶盐的溶解度 例题在298K时,测量BS),饱和溶液在电导池中的电阻,得到这个溶液 的电导率为4.20×10S·m1。已知在该温度下,水的电导率为1.05× 10S·m',试求BaSO,在该温度下饱和溶液的浓度 解 K(BaSO,)=K(溶液)一K(H,O) =(4.20-1.05)×10-4Sm1=3.15×101Sm A(2Bas0,)≈4.(2Bas0】 =A(2Ba)+A(2s0) =(63.64+79.8)×10-Sm2mol =1.434×10-2Sm2mol c(zBaSO.)= k(BaSO,) Am(2BaS0,】 3.15×10Sm1 1.434X10 S.m.mol =2.197×102molm c(BaS())-c(BaSO)-1.099 X10-mol.m =1.099×105 mol.dm 所以,BaSO,在该温度下饱和溶液的浓度为1,099×10molm或1.099× 105 mol.dm 4.电导滴定 利用滴定过程中溶液电导变化的转折来确定滴定终点的方法称为电导滴 定。如图8.14所示,用NaOH溶液滴定HC1溶液,以电导率为纵坐标,加入的 NaOH的体积为横坐标。在加入NaOH前,溶液中只有HCl一种电解质,因为 H+的离子电导率很大,所以HCI溶液的电导率也很大。当逐渐滴人NaOH 后,溶液中H与加入的OH结合生成H,O。这个过程可以看作是电导率较小 的Na+取代了电导率很大的H*,因此整个溶液的电导率逐渐变小,见图(1)中 的AB段。当加人的NaOH恰与HCl的物质的量相等时溶液的电导率最小,见 图1)中的B点,即为滴定终点。当NaOH加入过量后,由于OH离子电导率 很大,所以溶液的电导率又增加了,见图(1)中的BC段。根据B点所对应的横 坐标上所用NaOH溶液的体积就可计算未知HCl溶液的浓度。 如以强碱(如NaOH)滴定弱酸(如HAc),开始时溶液的电导率很低,加入
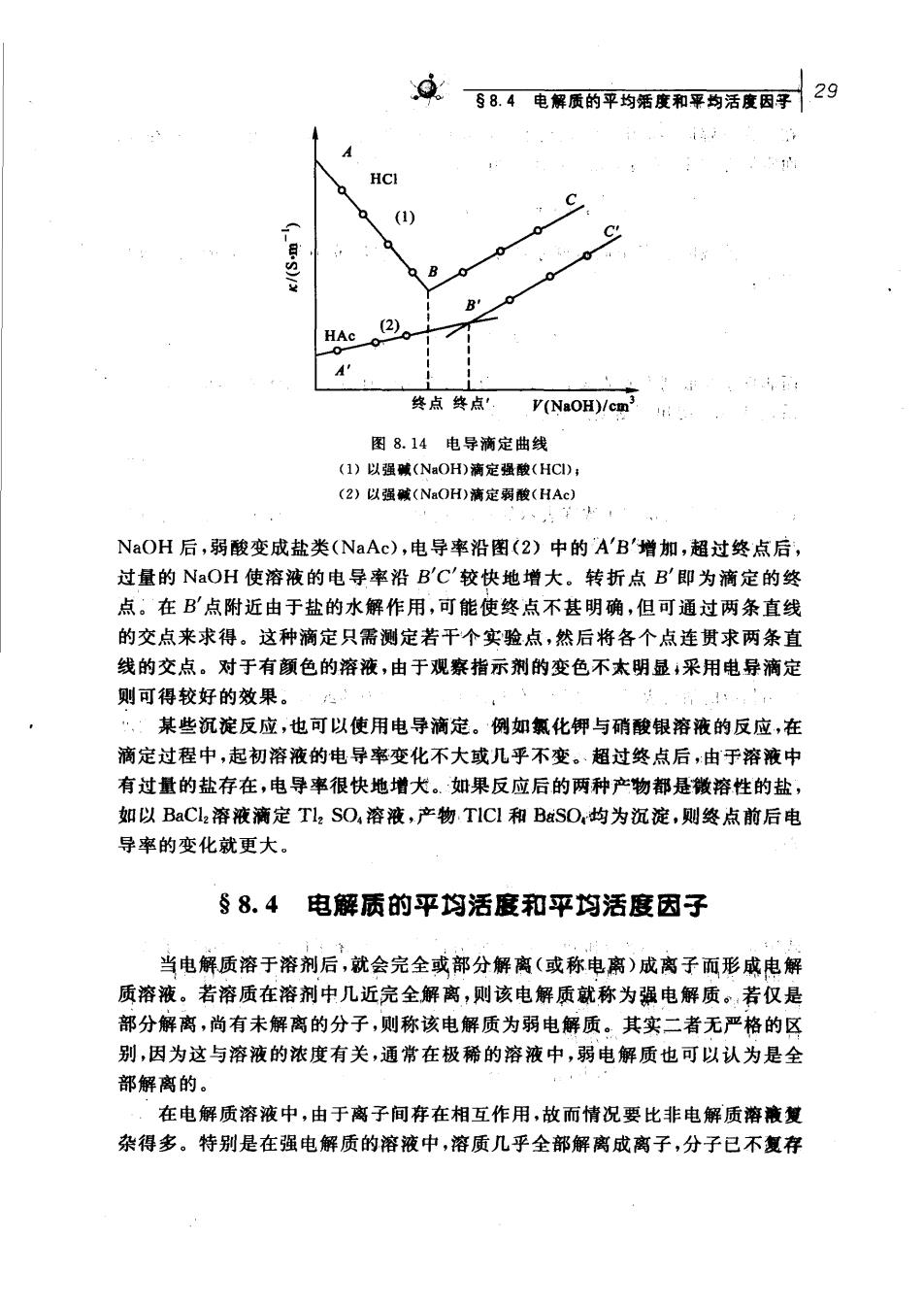
58.4电黑质的平均活度和平均活度因子29 A HCI () 31/ B B HAc②。 终点终点'V(NaOH)/cm 图8.14电导滴定曲线 (1)以强碱(NOH)流定强酸(H) (2)以强碱(NaOH)清定弱酸(HAc) NaOH后,弱酸变成盐类(NaAc),电导率沿图(2)中的A'B'增加,超过终点后 过量的NaOH使溶液的电导率沿B'C'较快地增大。转折点B'即为滴定的终 点。在B点附近由于盐的水解作用,可能使终点不甚明确,但可通过两条直线 的交点来求得。这种滴定只需测定若干个实验点,然后将各个点连贯求两条直 线的交点。对于有颜色的溶液,由于观察指示剂的变色不太明显,采用电异滴定 则可得较好的效果。 某些沉淀反应,也可以使用电导滴定。例如氯化钾与硝酸银溶液的反应,在 滴定过程中,起初溶液的电导率变化不大或儿乎不变。,超过终点后,由于溶液中 有过量的盐存在,电导率很快地增大。如果反应后的两种产物都是微溶性的盐, 如以BaC12溶液滴定Tl,SO,溶液,产物TlCl和BaSO,均为沉淀,则终点前后电 导率的变化就更大。 §8.4电解质的平均活度和平均活度因子 当电解质溶于溶剂后,就会完全或部分解离(或称电离)成离子而形成电解 质溶液。若溶质在溶剂中几近完全解离,则该电解质就称为强电解质。若仅是 部分解离,尚有未解离的分子,则称该电解质为弱电解质。其实二者无严格的区 别,因为这与溶液的浓度有关,通常在极稀的溶液中,弱电解质也可以认为是全 部解离的。 在电解质溶液中,由于离子间存在相互作用,故而情况要比非电解质溶液复 杂得多。特别是在强电解质的溶液中,溶质几乎全部解离成离子,分子已不复存

30第入束电聚质语有影 在。在电解质溶液中,正、负离子共存并且相互吸引,而不能自由地单独存在,故 而常需考虑正、负离子相互作用和相互影响的平均值。 电解质的平均活度和平均活度因子 当溶液的浓度用质量摩尔浓度表示时,理想溶液中某一组分的化学势可 写为: =(TD+RTa号 而非理想溶液则不遵从这个公式。为了使热力学计算仍然能保持简单的数学关 系式,Lewis提出了活度的概念,定义 a8=号 (8.29) 式中Y.B是以质量摩尔浓度表示的物质B的活度因子。当mg一0时,Ym.s→1, 对于非理想溶液,化学势的表示式为 (T)+RTIny.m (8.30) =唱(T)+RTlnam,B 这样,从理想溶液的公式出发所导得的一些热力学公式,只要把其中的浓度 项用相应的活度表示,就能用于任何溶液,包括理想的或非理想的溶液。若浓度 用c或x表示,则有与之对应的活度和活度因子(因电化学中用质量摩尔浓度 居多,故以下均以质量摩尔浓度为例讨论,并略去“m”下标)。 电解质溶液比非电解质溶液情况要复杂得多。强电解质溶于水后,几乎全 部电离成正、负离子,且离子间存在着静电引力。这样,对于各种正、负离子分 别有 4=+,a-=y% 式中a+(a-),y+(y-)和m+(m-)分别表示正(负)离子的活度、活度因子及离 子的质量摩尔浓度。现以1-1价型的HC1水溶液为例,表明离子的活度、活度 因子及质量摩尔浓度与整个电解质HCI的各种对应物理量之间的关系。设 HC!在稀水溶液中全部解离 HCl(aHc)-H+(aH+)+Cl(ac-) 解离前 uHcI=uRc (T)+RTInawc (8.31) 解离后 4H*=μ+(T)+RTlnag+ (8.32)

来雪84电邪质防平玛活夜和平鸡活度西子31 uor=u-(T)+RTInaa (8.33) 整个电解质(即HC)的化学势可以用各个离子的化学势之和来表示,即 Hc=H*十uaμa=+十品 (8.34) 将式(8.32)和式(8.33)代入式(8.34),得 uHc=(u+u)+RTIn (an+ac) -u+RTin (an'acr) 对照式(8.31),得 aHa=aH+aa- (8.35) 式中 am=mga=am号 现将HCl的正、负离子的平均活度a±(mean activity of ions).、平均质量摩尔浓 度m±(mean molality of ions)和平均话度因子yt(mean activity factor of ions). 分别定义为: a生址(an da)t (8.36a) n兰(ma)止 (8.36b) Y生世(ma)t (8.36c) a4=生特 (8.37) 上述平均值均为几何平均值,根据式(8.35),则应有 ana=ant aa-=a (8.38) 以上讨论的是1-1价型的电解质溶液,对于任意价型的强电解质B,设其化 学式为M,A,则应有 M,A,.→+M++u-A 式中z十和x一代表正、负离子的价数。与上述讨论的HC1类似: :u-u (T)+RTInan +u(T)+RTIna+ u-=u(T)+RTIna-. 因此 uB=++十-