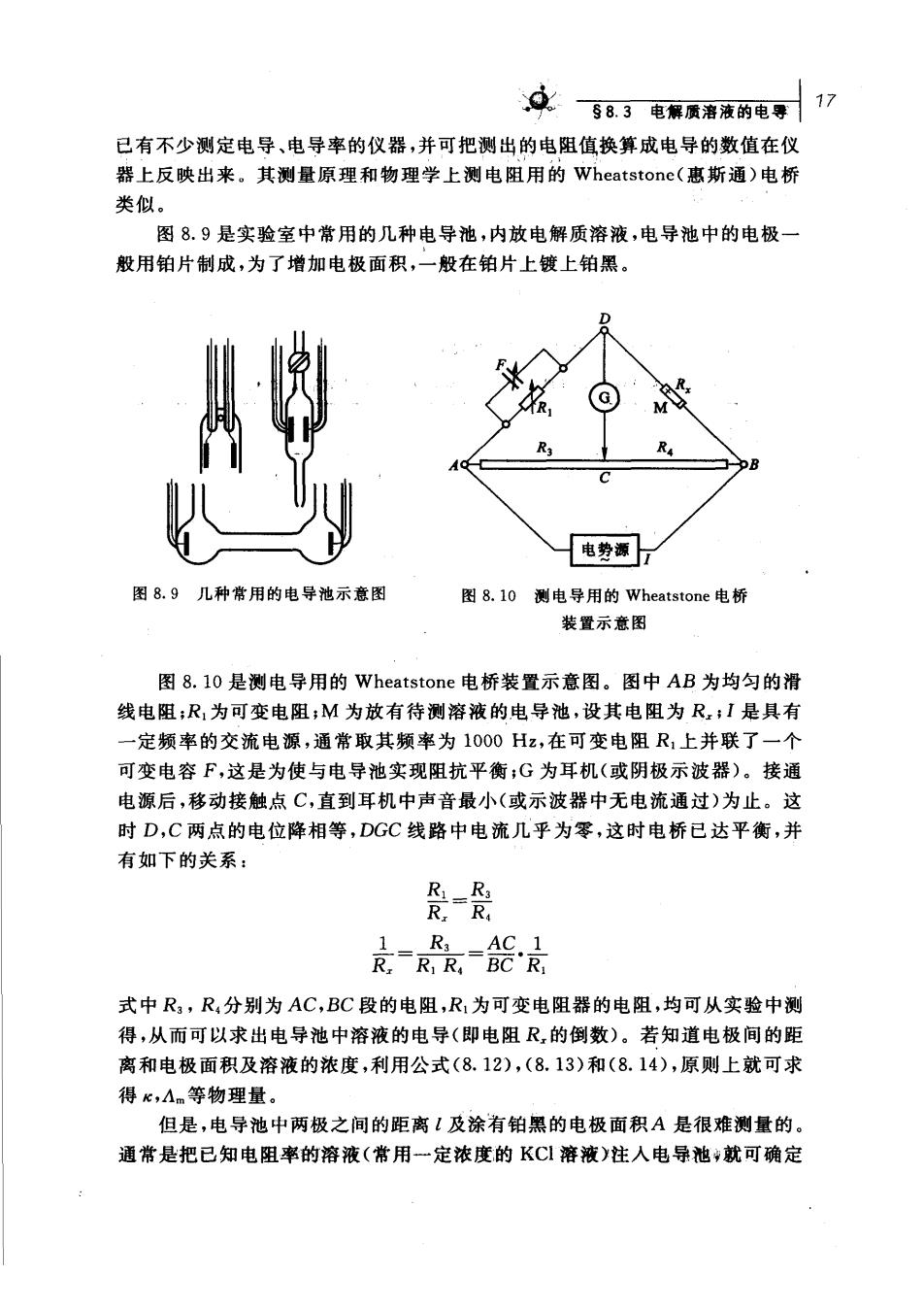
文58日电带质洛液的电琴17 已有不少测定电导、电导率的仪器,并可把测出的电阻值换算成电导的数值在仪 器上反映出来。其测量原理和物理学上测电阻用的Wheatstone(惠斯通)电桥 类似。 图8.9是实验室中常用的几种电导池,内放电解质溶液,电导池中的电极一 般用铂片制成,为了增加电极面积,一般在铂片上镀上铂黑。 电势源 图8.9几种常用的电导池示意图 图8.10测电导用的Wheatstone电桥 装置示意图 图8.l0是测电导用的Wheatstone电桥装置示意图。图中AB为均匀的滑 线电阻:R1为可变电阻,M为放有待测溶液的电导池,设其电阻为R;I是具有 一定频率的交流电源,通常取其频率为1000Hz,在可变电阻R1上并联了一个 可变电容F,这是为使与电导池实现阻抗平衡:G为耳机(或阴极示波器)。接通 电源后,移动接触点C,直到耳机中声音最小(或示波器中无电流通过)为止。这 时D,C两点的电位降相等,DGC线路中电流几乎为零,这时电桥已达平衡,并 有如下的关系: R.R 克x瓷完 式中R,R,分别为AC,BC段的电阻,R为可变电阻器的电阻,均可从实验中测 得,从而可以求出电导池中溶液的电导(即电阻R的倒数)。若知道电极间的距 离和电极面积及溶液的浓度,利用公式(8.12),(8.13)和(8.14),原则上就可求 得心,Am等物理量。 但是,电导池中两极之间的距离!及涂有铂黑的电极面积A是很难测量的 通常是把已知电阻率的溶液(常用一定浓度的KC1溶液)注人电导池就可确定
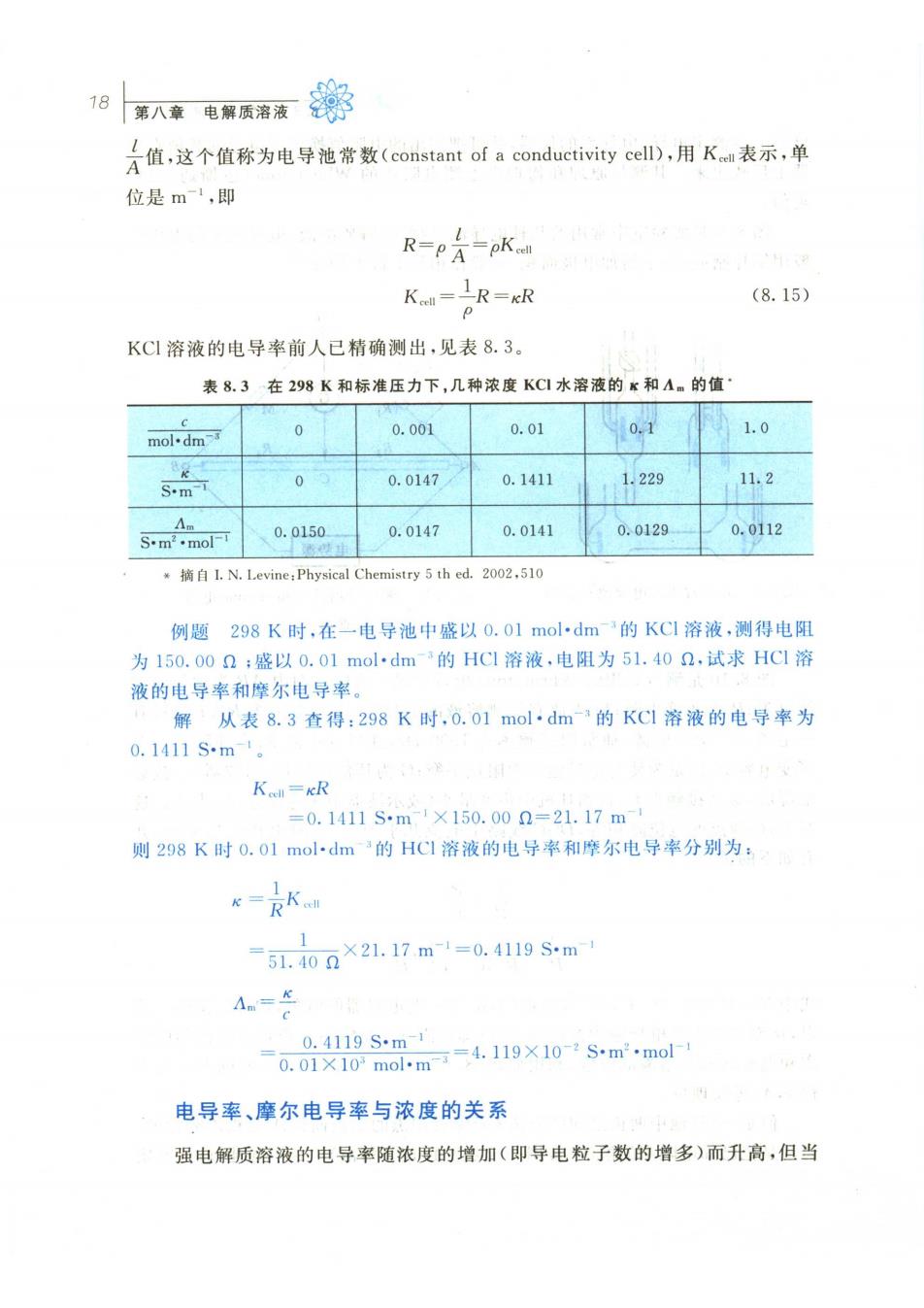
旧多八章电聚质带看黎 合值,这个值称为电导池常数(constant of a conductivityce),用Km表示,单 位是m1,即 R-pA-pK K.-IR-gR (8.15) KC1溶液的电导率前人已精确测出,见表8.3。 表8.3在298K和标准压力下,几种浓度KC水溶液的x和Am的值 mol.dm 0 0.00 0.01 0.1 1.0 0 0.0147 0.1411 1.229 11.2 Am S.m'.mol- 0.0150 0.0147 0.0141 0.0129 0.0112 I.N.Levine:Physical Chemistry 5 th ed.2002.510 例题298K时,在一电导池中盛以0.01mol·dm的KC1溶液,测得电阳 为150.000:盛以0.01mol·dm的HC1溶液,电阻为51.402,试求HCI溶 液的电导率和摩尔电导率。 解从表8.3查得:298K时,0.01mol·dm3的KC1溶液的电导率为 0.1411Sm Ko=R =0.1411Sm1×150.000=21.17m 则298K时0.01 mol-dm3的HC1溶液的电导率和摩尔电导率分别为: k-ka 51.40n×21.17m1=0.419sm An= 0.4119Sm 0.01×10molm=4.119×102Sm2mol 电导率、摩尔电导率与浓度的关系 强电解质溶液的电导率随浓度的增加(即导电粒子数的增多)而升高,但当
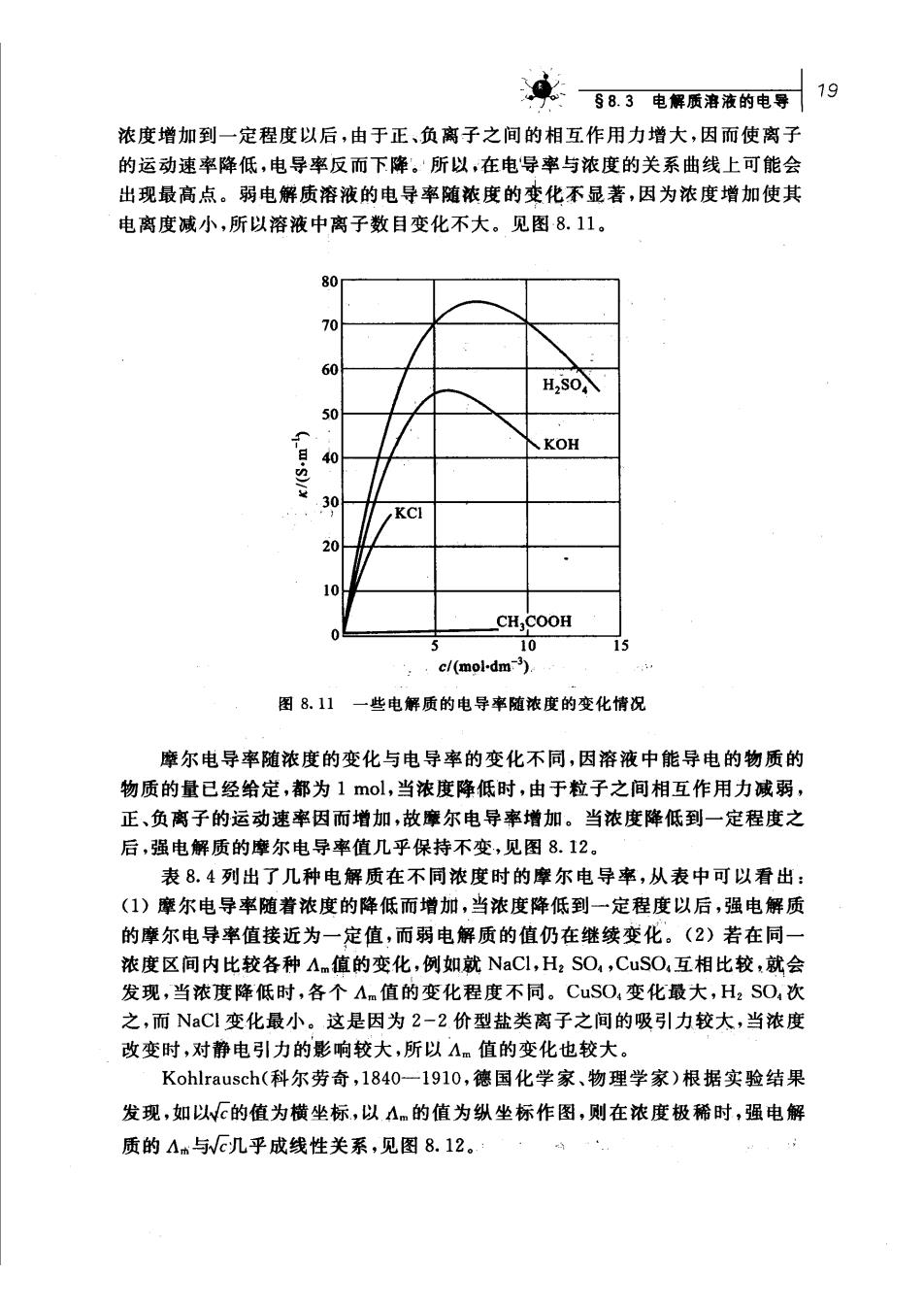
文:583电解质滑液的电号19 浓度增加到一定程度以后,由于正,负离子之间的相互作用力增大,因而使离子 的运动速率降低,电导率反而下降。所以,在电导率与浓度的关系曲线上可能会 出现最高点。弱电解质溶液的电导率随浓度的变化不显著,因为浓度增加使其 电离度减小,所以溶液中离子数目变化不大。见图8.11。 80 60 KOH KC 20 CH,COOH 10 c/(mol-dm). 图8.11 一些电解质的电导率随浓度的变化情况 摩尔电导率随浓度的变化与电导率的变化不同,因溶液中能导电的物质的 物质的量已经给定,都为1mol,当浓度降低时,由于粒子之间相互作用力诚弱, 正、负离子的运动速率因而增加,故摩尔电导率增加。当浓度降低到一定程度之 后,强电解质的摩尔电导率值几乎保持不变,见图8.12。 表8.4列出了几种电解质在不同浓度时的摩尔电导率,从表中可以看出: (1)摩尔电导率随着浓度的降低而增加,当浓度降低到一定程度以后,强电解质 的摩尔电导率值接近为一定值,而弱电解质的值仍在继续变化。(2)若在同一 浓度区间内比较各种Am值的变化,例如就NaCl,HzSO,CuSO,互相比较,就会 发现,当浓度降低时,各个A.值的变化程度不同。CuSO,变化最大,H,SO,次 之,而NaC1变化最小。这是因为2-2价型盐类离子之间的吸引力较大,当浓度 改变时,对静电引力的影响较大,所以A。值的变化也较大。 Kohlrausch(科尔劳奇,l840一1910,德国化学家、物理学家)根据实验结果 发现,如以N的值为横坐标,以Am的值为纵坐标作图,则在浓度极稀时,强电解 质的A与儿乎成线性关系,见图8.12
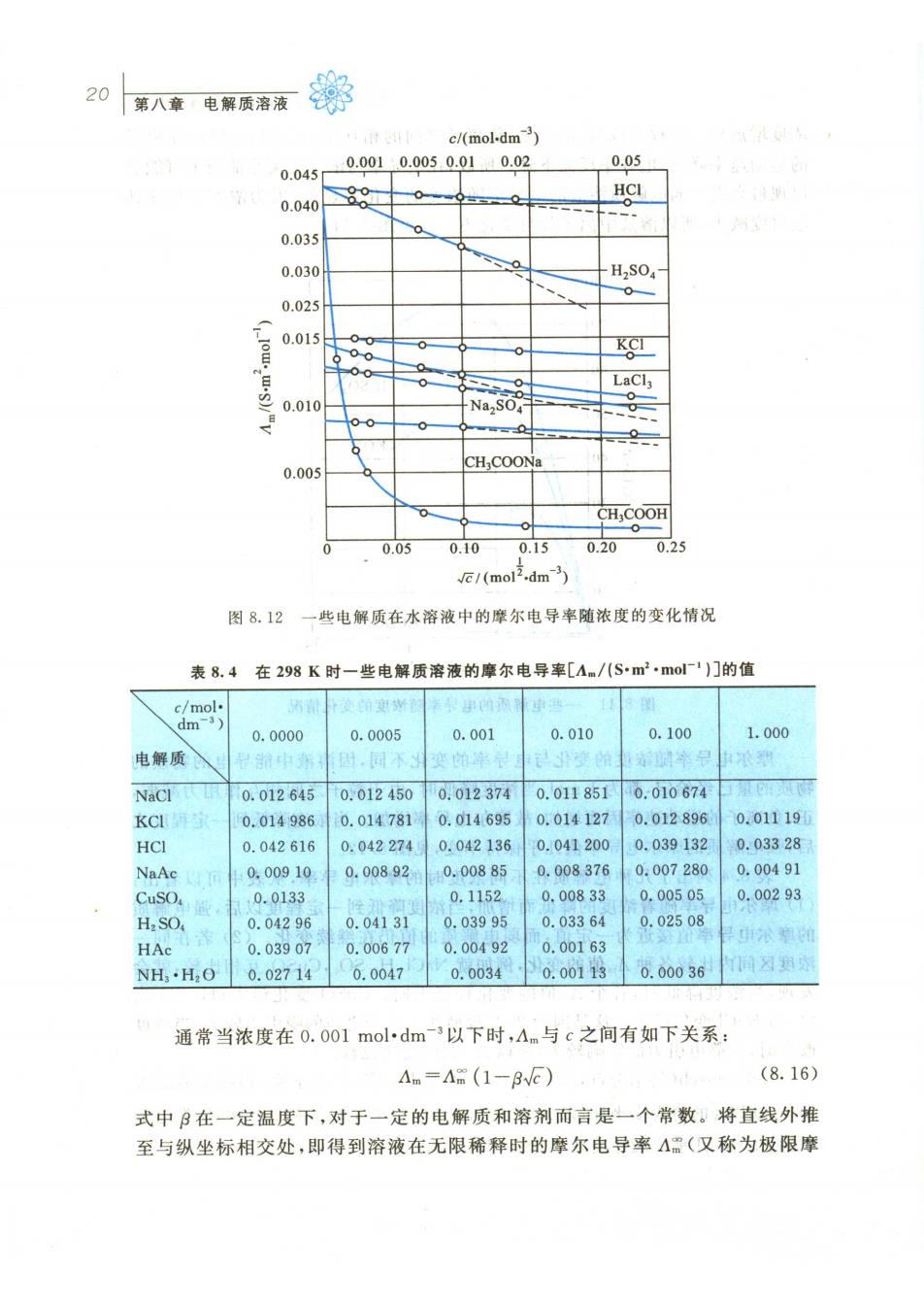
20 八电质有 c/(mol-dm) 0.045 0.0010.0050.010.0 0.05 0.0408 HCI 0.035 0.030 H.so. 0.02 0015 LaCl 0.01 Na SO .005 CH COON H.COOH 0.05 0.10 0.15 0.20 025 /(mol.dm) 图8.12 一些电解质在水溶液中的摩尔电导率随浓度的变化情况 表8.4在298K时一些电解质溶液的摩尔电导率[4m/八Sm2·mo')门的值 0.0000 0.0005 0.001 0.010 0.100 1.000 电解质 0.01264 0.0124500.0123740.0118510.010674 KCI 0.014986 0.0147810.01469 0.01412 0.012896 0.01119 HCI 0.042616 0.0422740042136 0.041200 0.039132 0,03328 NaAc 0.00910 0.00892 0.00885 0.008376 0007280 0.00491 0.0133 0.1152 0,0083 0,0050 0.00293 H:SO 0.04296 0.04131 0.03995 0.03364 0.02508 HA 003907 0.00677 0.00492 0.00163 NH·HO 0.027140.0047 0.0034 0.001130.00036 通常当浓度在0.001 mol.dm-3以下时,A.与c之间有如下关系 Am=A(1-8vc) (8.16) 式中B在一定温度下,对于一定的电解质和溶剂而言是一个常数。将直线外推 至与纵坐标相交处,即得到溶液在无限稀释时的摩尔电导率A品(又称为极限摩
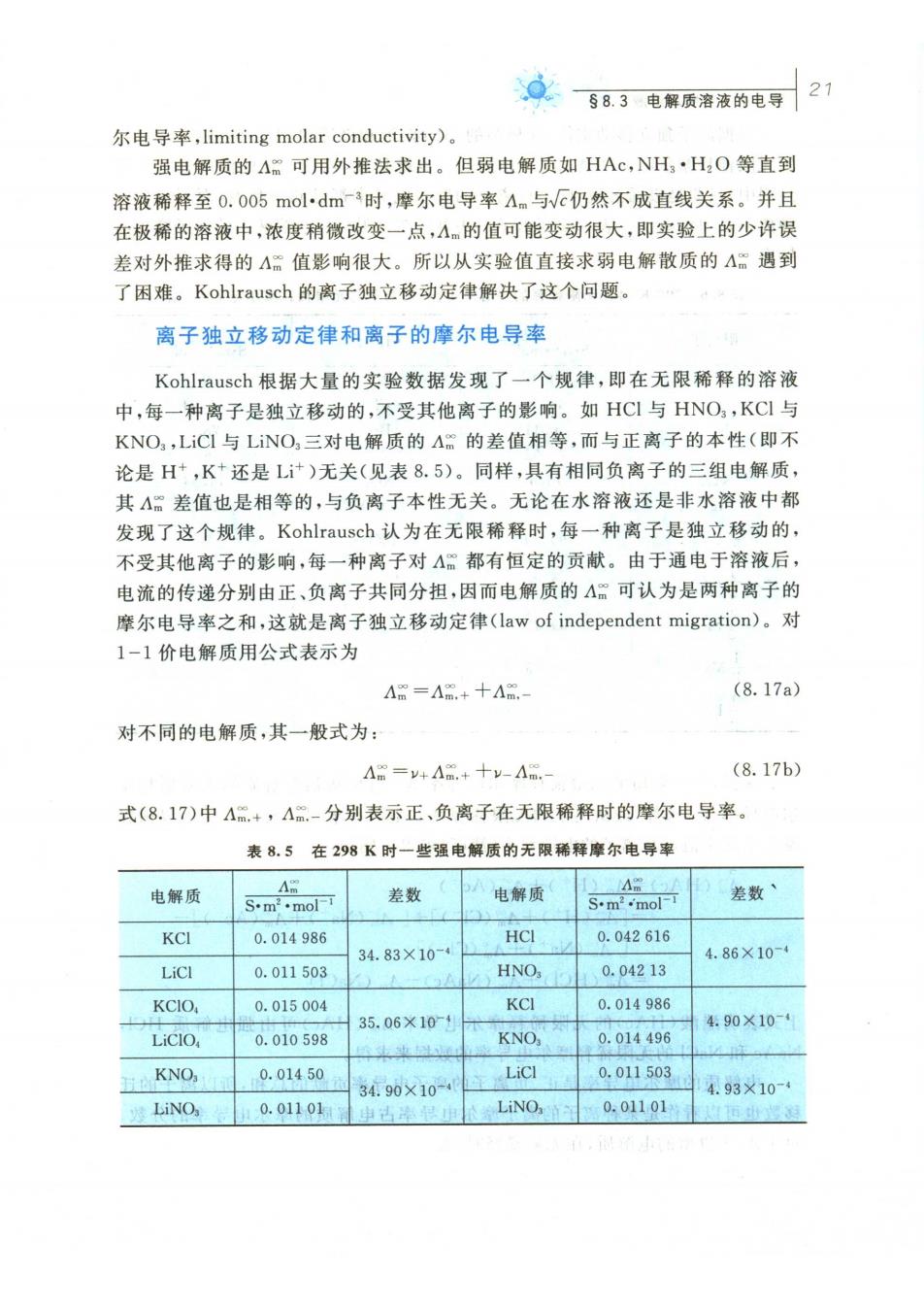
众683电解质溶液的电导 21 尔电导率,limiting molar conductivity) 强电解质的A可用外推法求出。但弱电解质如HAc,NH·H2O等直到 溶液稀释至0.005mol·dm-3时,摩尔电导率Am与VE仍然不成直线关系。并且 在极稀的溶液中,浓度稍微改变一点,Am的值可能变动很大,即实验上的少许误 差对外推求得的A:值影响很大。所以从实验值直接求弱电解散质的A遇到 了困难。Kohlrausch的离子独立移动定律解决了这个问题。 离子独立移动定律和离子的摩尔电导率 Kohlrausch根据大量的实验数据发现了一个规律,即在无限稀释的溶液 中,每一种离子是独立移动的,不受其他离子的影响。如HCI与HNO,KC与 KNO,LiC1与LiNO,三对电解质的A的差值相等,而与正离子的本性(即不 论是H,K+还是L计)无关(见表8.5)。同样,具有相同负离子的三组电解质 其A差值也是相等的,与负离子本性无关。无论在水溶液还是非水溶液中都 发现了这个规律。Kohlrausch认为在无限稀释时,每一种离子是独立移动的, 不受其他离子的影响,每一种离子对△。都有恒定的贡献。由于通电于溶液后 电流的传递分别由正、负离子共同分担,因而电解质的A云可认为是两种离子的 摩尔电导率之和,这就是离子独立移动定律(law of independent migration)。对 1-1价电解质用公式表示为 (8.17a) 对不同的电解质,其一般式为: Am=+Am+十-Am (8.17b) 式(8.17)中A“+,A-分别表示正、负离子在无限稀释时的摩尔电导率。 表8.5在298K时一些强电解质的无限稀释摩尔电导率 电解质 S.mmol 差数 电解质 S.m mol 差数 KCI 0.014986 HCI 0.042616 34.83×10-4 4.86×10 0.011503 HNO, 0.04213 KCIO, 0.015004 KCI 0.014986 35.06X10-1 4.90×10-4 0.010598 KNO, 0.014496 KNO, 0.01450 LiCl 0.011503 3490×10-4 403×10- 发LiNO 0.01101 LiN030.01101