
12八食电限质洛资券 2Cm++e一2cu() 。Cu(s)在阴极区的物质的量的变化为: 已知2CuS0,的摩尔质量为M(2CuS0)=79.75gmol,银的摩尔质量为 M(Ag)=107.88gmol1,则 1.1090 "sfT79.,75gm6=l.3906X10mol 1.1276g ms=79.75gm0=1.4139X102mol ma107.88gnm0=3.751×10ml 0.0405g 刀证移二刀了一刀起十电 =[(1.3906-1.4139)×10+3.754×10]mol =1.424×10-mol t-=1-t4年1-0.38=0.62 如果首先计算S(离子的迁移数,阴极部S0离子浓度的改变只是由于 S)离子的迁出造成的,S心离子在阴极上不发生化学反应,故号SO在阴 极部物质的量的变化为: 力修r=刀起始一刀旺移 刀证移一刀显始一1降了 =[(1.4139-1.3906)×102]mol=2.33×10-mol t4=1-t=0.38 如果选取C作为基本质点,其余的计算方法完全相同,只是库仑计中对 应的两个银的摩尔质量为M(2Ag)=107.88gmo'×2,这样计算得到的迁移 数是一样的。 Hittorf法的原理简单,但在实验过程中很难避免由于对流、扩散、振动等引 起溶液相混,所以不易获得准确结果。另外,在计算时没有考虑水分子随离子的

2离子的电正移率和迁移数13 迁移,这样得到的迁移数常称为表观迁移数(apparent transference number或称 Hittorf迁移数)。 2.界面移动法 界面移动法简称界移法(boundary 熹安培计 moving method),此法能获得较为精确的 结果。它是直接测定溶液中离子的移动速 率(或淌度)。这种方法所使用的两种电解 质溶液具有一种共同的离子,它们被小心 电明 地放在一个垂直的细管内,利用溶液密度 HCI- 的不同,使这两种溶液之间形成一个明显 的界面(通常可以借助于溶液的颜色或折 可变电阻 射率的不同使界面清晰可见)。如图8.6cdC, 所示。在管中先放CdCl,溶液,然后再小心 放入HCI溶液,形成bb界面。在通电过程 人心电香仅 中,C从阳极上溶解下来,H,(g)在上面阴图8.6界面移动法测定迁移数装置 极上放出,溶液中H*向上移动,bb界面也 上移。由于C+的淌度比H+小,C+跟在H之后向上移动,所以不会产生 新的界面。根据管子的横截面积、在通电的时间内界面移动的距离及通过该电 解池的电荷量就可计算出离子的迁移数。 例题参阅图8.6.设玻璃管的横截面积为1.0×10m,HC1的浓度为 10.0mol·m,当通以0.01A的电流,历时200s后,界面从bb移到aa',移动 了0.17m,求H的迁移数。 解在bb与aa'区间内的H离子,均通过aa面而上移,设这个区间的体 积是V,通过a'面的H离子的个数为cV,它所迁移的电荷量为 cVL3e=3cVF 经历时间:后通人的总电荷量为,根据迁移数的定义 -H能-严 通过的总电荷量 -1×10.0 mol.mx(0.17×1.0×10)m3×96500C·mol 0.01C·s1×200s =0.82 在图8.6中,CCl2溶液的作用是作为指示溶液,Cd+的移动速率不能大于 H的移动速率,否则会使界面模糊不清。要使界面清晰,两种离子的移动速率 应尽可能接近
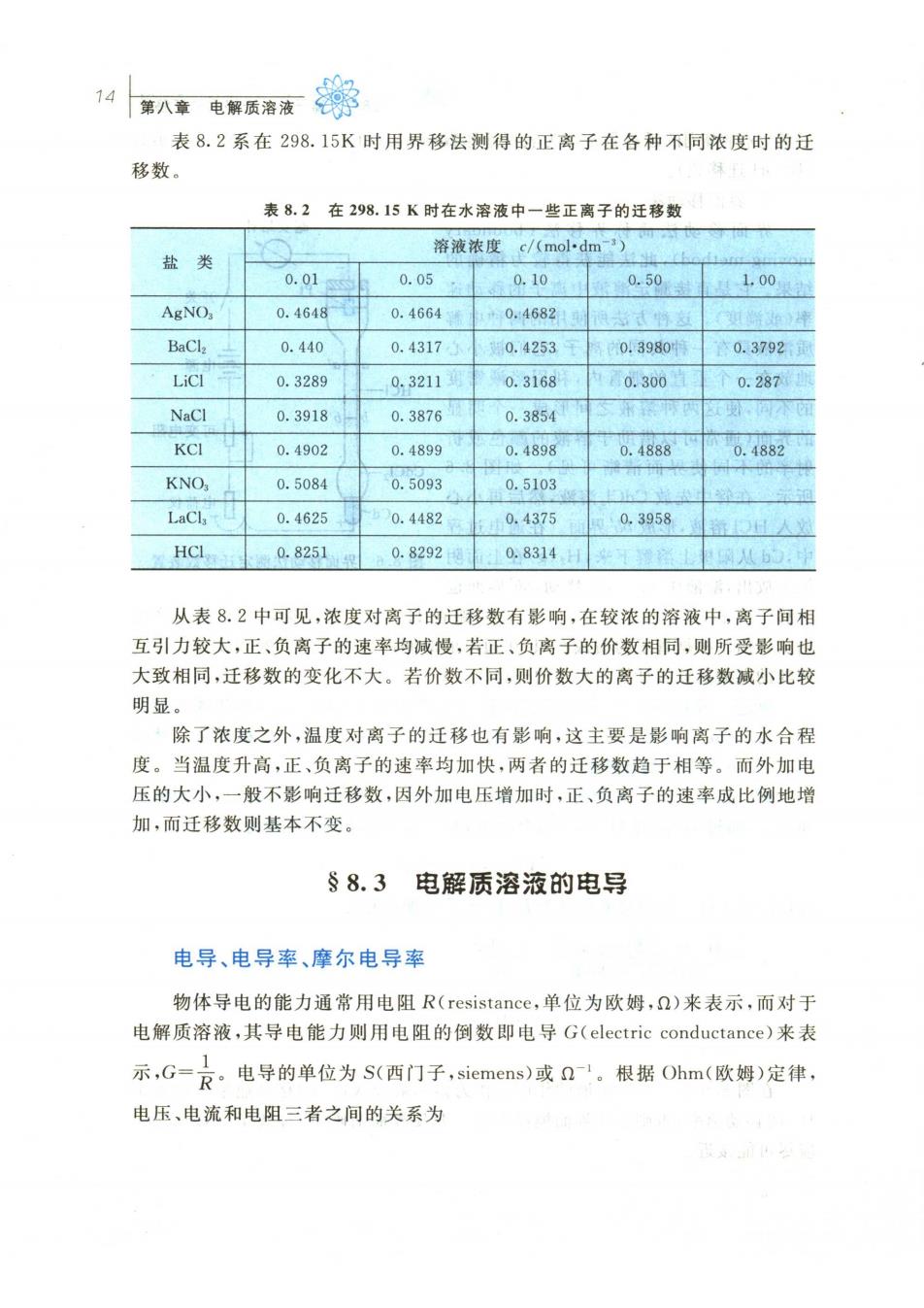
14 表8.2系在298.15K时用界移法测得的正离子在各种不同浓度时的迁 移数。 表8.2在298.15K时在水溶液中一些正离子的迁移数 溶液浓度c/(mol·dm) 盐类 0.01 0.05 0.10 0.50 100 AgNO, 0.4648 0.4664 +0.46821 BaCla 0.440 0.43175 150.4253¥0.3980 次0.3792日 LiCl 0.3289 -0,32113期 0.31680.300 0.287 NaCl 0.3918 0.3876 0.3854 KCI 0.4902 0.4899 0.48980.488 0.4882 KNO 0.5084 0.5093 0.5103 0.4625 0.4482 0.437500,3958 HCl 0.8251 0.82920.8314H165 从表8.2中可见,浓度对离子的迁移数有影响,在较浓的溶液中,离子间相 互引力较大,正、负离子的速率均减慢,若正、负离子的价数相同,则所受影响也 大致相同,迁移数的变化不大。若价数不同,则价数大的离子的迁移数减小比较 明显。 除了浓度之外,温度对离子的迁移也有影响,这主要是影响离子的水合程 度。当温度升高,正、负离子的速率均加快,两者的迁移数趋于相等。而外加电 压的大小,一般不影响迁移数,因外加电压增加时,正、负离子的速率成比例地增 加,而迁移数则基本不变。 §8.3电解质溶液的电导 电导、电导率、摩尔电导率 物体导电的能力通常用电阻R(resistance,单位为欧姆,Q)来表示,而对于 电解质溶液,其导电能力则用电阻的倒数即电导G(electric conductance)来表 示,G=。电导的单位为S(西门子,siemens)或'。根据Ohm(欧姆)定律, 电压、电流和电阻三者之间的关系为
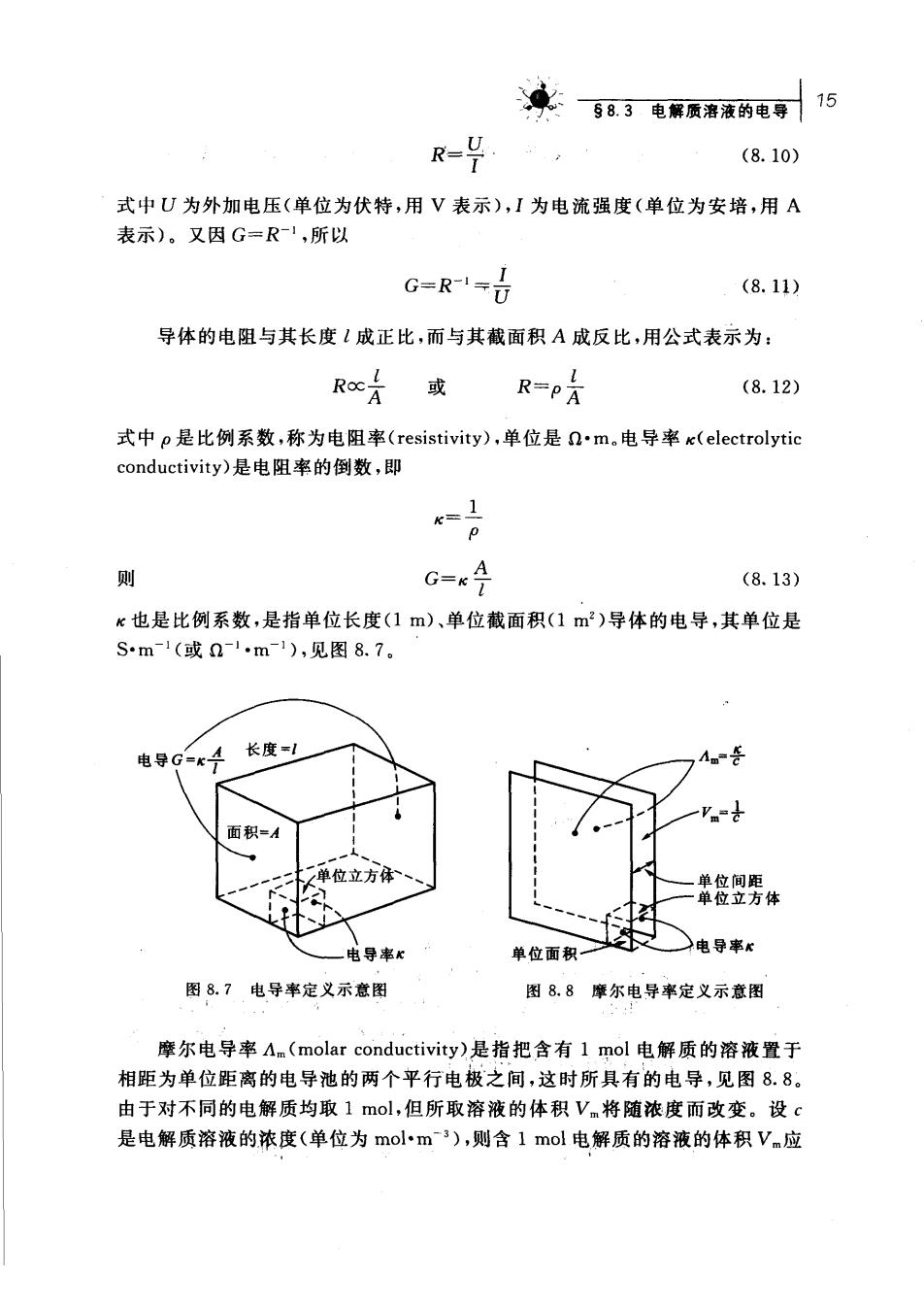
来583电限预潘液的电存15 R=兴 (8.10) 式中U为外加电压(单位为伏特,用V表示),I为电流强度(单位为安培,用A 表示)。又因G=R1,所以 G=R1= (8.11) 导体的电阻与其长度1成正比,而与其截面积A成反比,用公式表示为: Roc片 或 R=P月 (8.12) 式中p是比例系数,称为电阻率(resistivity),单位是nm.电导率e(electrolytic conductivity)是电阻率的倒数,即 =日 奥 G-x4 (8.13) K也是比例系数,是指单位长度(1m)、单位截面积(1m)导体的电导,其单位是 Sm-1(或n-1m-1),见图8.7。 导 G-K4 长度 面积=A ,单位立方体 染倍园秀体 电导率心 单位面积一 )电导率x 图8.7电导率定义示意图 图8.8摩尔电导率定义示意图 摩尔电导率An(molar conductivity)是指把含有1mol电解质的溶液置于 相距为单位距离的电导池的两个平行电极之间,这时所具有的电导,见图8.8。 由于对不同的电解质均取1mol,但所取溶液的体积Vm将随浓度而改变。设G 是电解质溶液的浓度(单位为mol小m3),则含1mol电解质的溶液的体积Vm应

16第八电系质帝液家 等于二,根据电导率x的定义,摩尔电导率A与电导率x之间的关系用公式表 示为 A= (8.14) 因为x的单位为S·m1,c的单位为mol·m3,所以摩尔电导率Am的单位为 Sm2mol1。 例题在291K时,浓度为10mol·m3的CuSO,溶液的电导率为 0.1434Sm',试求CuSO,的摩尔电导率A.(CuS),)和。CuSO),的摩尔电导率 A.(2CuS()) 解 A (CuSO)=(CuSO. -0,1434sm=14.34×10Sm2mol 10 mol.m Am(2Cus0,)= (2cuso】 =2x10m0:m=7.17×10 S.m.mol 0.1434Sm 注意:(1)当浓度c的单位是以mol.dm表示时,则要换算成以mol·m 表示,然后进行计算。即在数字运算的同时,单位也进行运算,才能获得正确的 结果。 (2)在使用摩尔电导率这个量时,应将浓度为c的物质的基本单元置于A。 后的括号中,以免出错。例如,A(CuS0,)和A(2CuS0,)都可称为摩尔电号 率,只是所取的基本单元不同,显然A(CuS),)=2A.(号CuSO,) 引入摩尔电导率的概念是很有用的。因为一般电解质的电导率在不太浓的 情况下都随着浓度的增高而变大,因为导电粒子数增加了。为了便于对不同类 型的电解质进行导电能力的比较,人们常选用摩尔电导率,因为这时不但电解质 有相同的量(都含有1mol的电解质),而且电极间距离也都是单位距离。当然, 在比较时所选取的电解质基本粒子的荷电荷量应相同。 电导的测定 电导的测定在实验中实际上是测定电阻。随着实验技术的不断发展,目前