
众58:2离子的电迁移率和迁移数7 例题需在10×10cm的薄铜片两面镀上0.005cm厚的Ni层[镀液用 N(NO):溶液],假定镀层均匀分布,用2.0A的电流得到上述厚度的镍层需通 电多长时间?设电流效率为96.0%。已知金属镍的密度为8.9gcm.Ni(s) 的摩尔质量为58.69gmol 解电极反应为: Ni'(aq)+2e -Ni(s) 镀层中含Ni(s)的质量为: 10×10cm×2X0.005cm×8.9gcm3=8.9g 按所写电极反应,析出8.9gN(s)的反应进度为」 8.9g 58.69 gmol=0.152ml 理论用电荷量为: Q=xFe=2×96500C·mol1×0.152mol=2.9×10C 实际用电荷量为:Q(实际)=2.9X10C=3.0X10C 0.96 通电时间为:1=Q(实际)=号0X10S=1.5×10≈4.2h 2.0C.s §8.2离子的电迁移率和迁移数 离子的电迁移现象 离子在外电场的作用下发生定向运动称为离子的电迁移(electromigra- tio)。当通电于电解质溶液之后,溶液中承担导电任务的阴、阳离子分别向阳、 阴两极移动,并在相应的两电极界面上发生氧化或还原作用,从而两极旁溶液的 浓度也发生变化。这个过程可用图8.3来示意说明。 设想在两个惰性电极之间的溶液中,有想象的平面AA和BB,将溶液分为 阳极部、中部及阴极部三个部分。假定在未通电前,各部分均含有都为一价的 正,负离子各5mol,分别用十,一号的数量来表示正、负离子的物质的量。今有 4mol电子的电荷量通过之后,在阳极上有4mol负离子发生氧化反应,同时在 阴极上有4mol正离子发生还原反应,在溶液中的离子也同时发生迁移。当溶 液中通过4mol电子的电荷量时整个导电任务是由正、负离子共同分担的,每种 离子所迁移的电荷量随着它们迁移的速率不同而不同(因已设离子所带的电荷
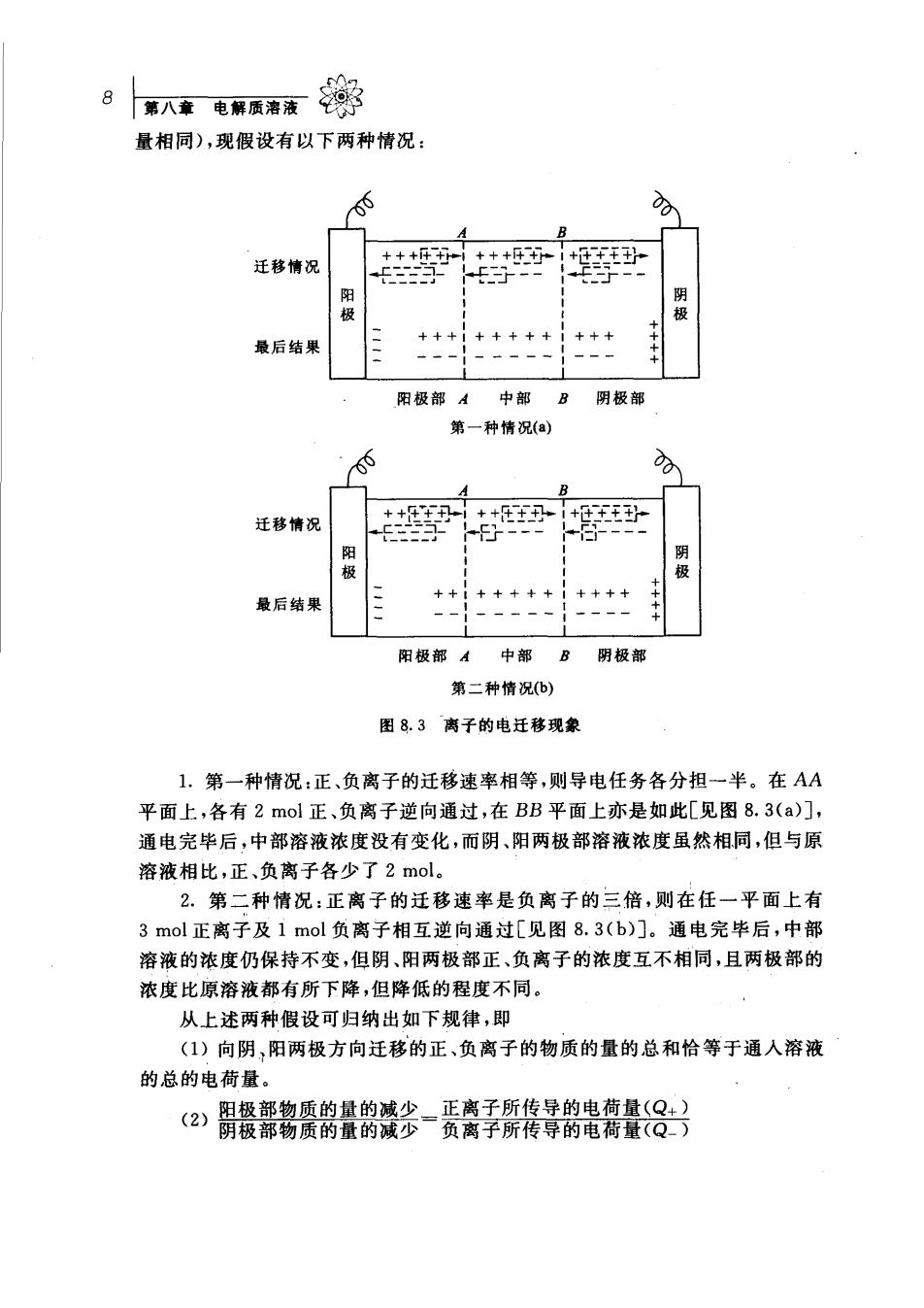
量相同),现假设有以下两种情况: 00 B 迁移情识 +++ +++ 阳极 最后结果 +++i+++++i+++ 阳极部A中部B阴极部 第一种情况(a) 0 y 迁移情况 ++ +王 +++ 最后结果 阳极部A中部B阴极部 第二种情况b) 图8.3离子的电迁移现象 1.第一种情况:正、负离子的迁移速率相等,则导电任务各分担一半。在AA 平面上,各有2mol正、负离子逆向通过,在BB平面上亦是如此[见图8.3(a)], 通电完毕后,中部溶液浓度没有变化,而阴、阳两极部溶液浓度虽然相同,但与原 溶液相比,正、负离子各少了2mol。 2.第二种情况:正离子的迁移速率是负离子的三倍,则在任一平面上有 3mol正离子及1mol负离子相互逆向通过[见图8.3(b)]。通电完毕后,中部 溶液的浓度仍保持不变,但阴、阳两极部正、负离子的浓度互不相同,且两极部的 浓度比原溶液都有所下降,但降低的程度不同。 从上述两种假设可归纳出如下规律,即 ()向阴,阳两极方向迁移的正、负离子的物质的量的总和恰等于通入溶液 的总的电荷量。 (2)關餐部铭爱鹄量韵餮多-贡资手所传寻鹤老离量8

众582离子的电廷移率和移数 上述讨论的是惰性电极的情况。若电极本身也参加反应,若正、负离子的电 荷量不同,则阴、阳两极溶液浓度变化情况要复杂一些。可根据电极上的具体反 应进行分析。 离子的电迁移率和迁移数 离子在电场中运动的速率除了与离子的本性(包括离子半径、离子水化程 度、所带电荷等)以及溶剂的性质(如黏度等)有关以外,还与电场的电位梯度 (electric potential gradient)dE/dl有关,显然电位梯度越大,离子运动的推动力 也越大,因此离子的运动速率可以写作: (8.2) 式(8.2)中的比例系数u+和4-相当于单位电位梯度(1V·m)时离子的运动速 率,称为离子电迁移率(又称为离子淌度,ionic mobility),单位为m2·s1.V-1 离子电迁移率的大小与温度、浓度等因素有关,它的数值可用界面移动实验来测 定(见下节)。表8.1列出了在298.15K无限稀释时几种离子的电迁移率。 由于正、负离子移动的速率不同,所带电荷不等,因此它们在迁移电荷量时 所分担的份额也不同。把离子B所运载的电流与总电流之比称为离子B的迁 移数(transference number),用符号tB表示,其定义式为: (8.3) 是离子B迁移电荷量的分数,其单位为1。 表8.1298.15K时一些离子在无限稀释水溶液中的离子电迁移率 正离子 围,中负离子 H+ 36.30 20.52 8) OH K 7.62 SO阳 8.27 Ba+ 6.59 CI 5.19 89 7.40 4.01 HCO 4.61 如图8.4所示,设有距离为1面积为A的两个平行铂电极,左方为阴极,右 方为阳极,外加电压为E,在电极间充以电解质为(M,N,)的溶液,其浓度为(

10入事电系质有擦 (单位为molm3),设它的解离度为a,则 M,N,=rM++yN c(1-a). cxa cya 如果正离子的迁移速率为r+,则单 位时间向阴极移动通过任意截面 SS,正离子所迁移的电荷量为: 82=1,=(cxa+Ar+)F (8.4a) 图8.4离子的电迁移 同理,负离子所迁移的电荷量为: Q-1-(cxas-Ar-)F (8.4b) 因为溶液总是电中性的,x之+=y2-,所以在单位时间内通过任一截面的总电 量为: 9-%+9=1,+1=1 I=(cxaz+Ar++cyaz-Ar-)F =cxa2+A(r+十r-)F =cyaz-A(r++r-)F (8.5) 根据迁移数的定义,则正、负离子的迁移数分别为 t+=7=+十r 1=r (8.6) 由于正、负离子处于同一电位梯度中,因此式(8.6)又可写作 t+=u+十w 4+ t-=u+十u 4- (8.7) 从式(8.6)和式(8.7)可得: ±=r土=《± (8.8) t-r-'u- t++t-=1 (8.9) 若溶液中的正、负离子不止一种,则任一离子B的迁移数为:

¢58,2离子的电迁移串和迁移敬 11 ∑=∑t4+∑t=1 “离子迁移数的测定 迁移数的测定最常用的方法有以下几种:(1)Hittorf(希托夫)法,(2)界面 移动法,(3)电动势法等(电动势法将在第9章中讨论)。 1.Hittorf法 图8.5是Hittorf法的实验装置示 意图。在管内装有已知浓度的电解质 电一 可变电阻 溶液,接通电源,适当控制电压,让很小 电流计 量 的电流通过电解质溶液,这时正、负离 子分别向阴、阳两极迁移,同时在电极 上有反应发生,致使电极附近的溶液浓 度不断改变,而中部溶液的浓度基本不 变。通电一段时间后,把阴极部(或阳 极部)的溶液小心放出,进行称量和分 析,从而根据阴极部(或阳极部)溶液中 电解质含量的变化及串联在电路中的 电荷量计上测出的通过的总电荷量,就 可算出离子的迁移数。若有的离子只 发生迁移而并不在电极界面上反应,则 其迁移数的计算就更为简单。通过下图8.5 Hittorf法测定迁移数的装置 面的例题可以了解迁移数的计算方法。 例题设在Hittorf迁移管中用Cu电极来电解已知浓度的CuSO,溶液,溶 液中通以20mA的直流电约2~3h,通电完毕后,串联在电路中的银库仑计阴 极上有0.0405g银析出。阴极部溶液的质量为36.434g,据分析知,在通电前 其中含CuS0,1.1276g,通电后含CuS0,1.1090g试求Cu2+和S)离子的 迁移数。 解分析阴极部的溶液浓度的变化,首先计算C+离子的迁移数。阴极部 Cu+离子浓度的改变是由两种原因引起的:(1)Cu离子的迁入,(2)Cu+离 子在阴极上发生还原反应。现在选取2C+作为基本质点,2C在阴极上发 生还原反应的方程式为: