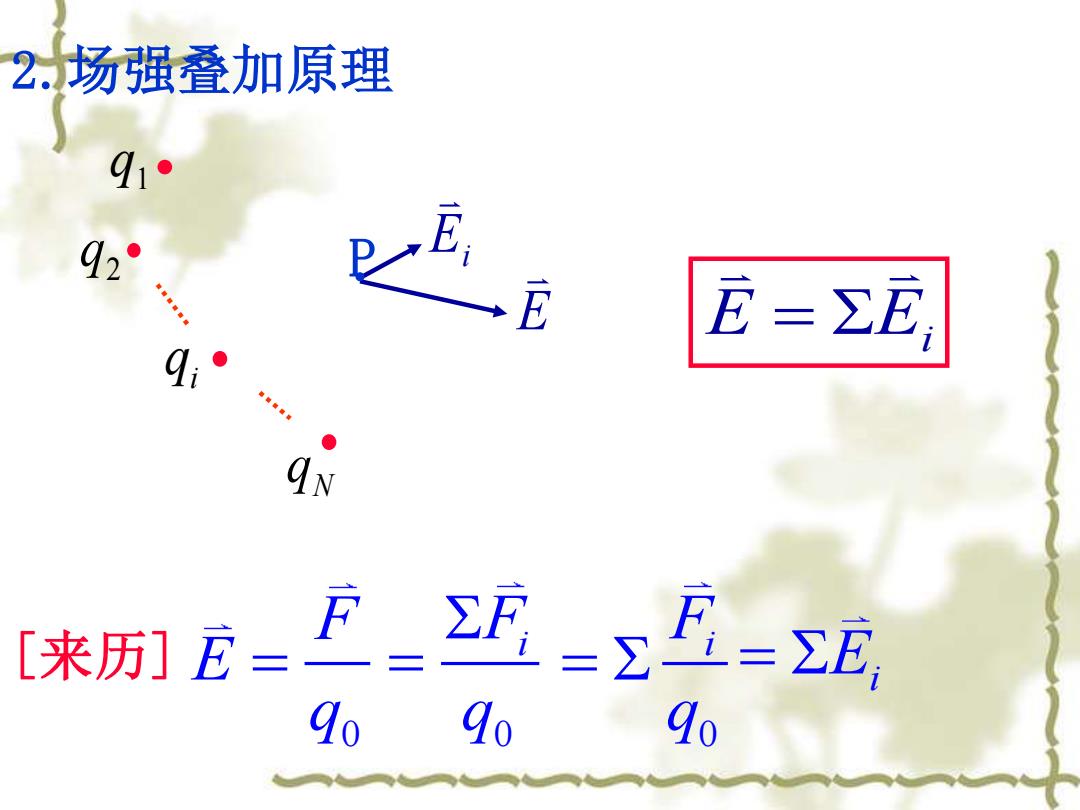
2.场强叠加原理 92° E=乃E, 9 ● [来历]龙= F_5-zE=ΣE 9090 9o
2.场强叠加原理 E Ei = q1 2 q E i q N q Ei P [来历] 0 F E q = = Ei 0 Fi q = 0 Fi q =

电荷连续分布情形: E= 电荷元dq产生的场强 Note: 点电荷场强十场强叠加原理=计算场 强的基本方法
电荷连续分布情形: E = dE 点电荷场强+场强叠加原理=计算场 强的基本方法 电荷元dq产生的场强 Note:
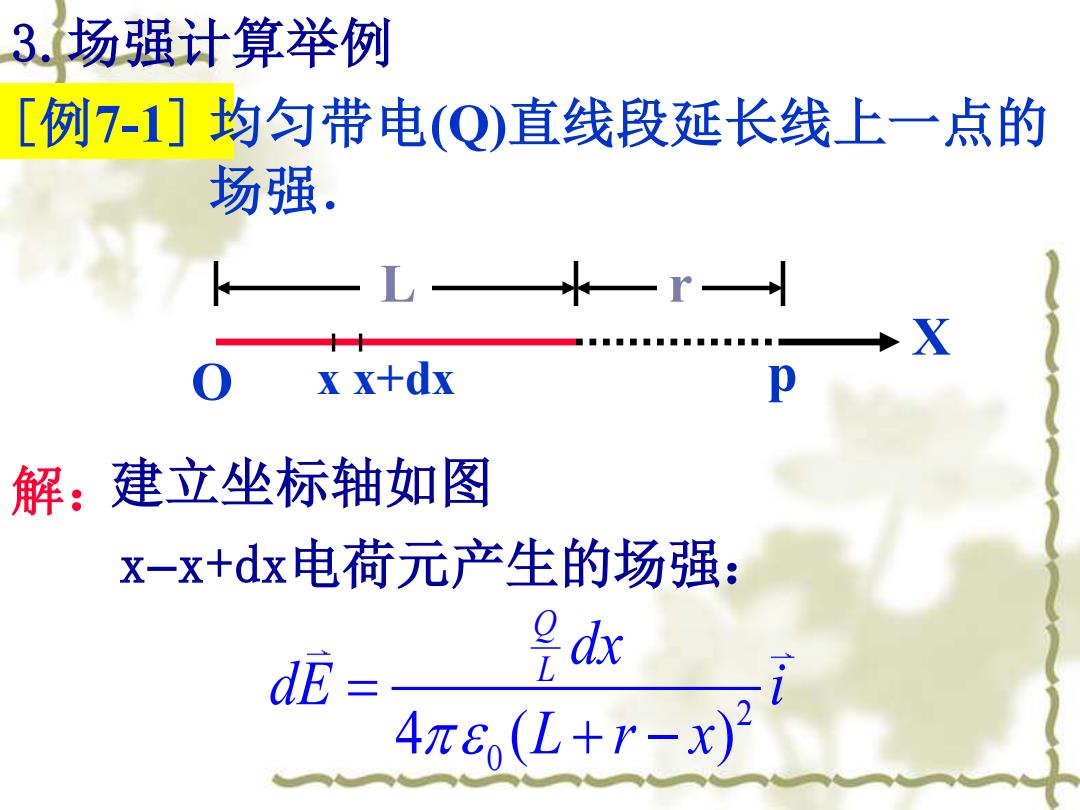
3.场强计算举例 [例7-1]均匀带电(Q)直线段延长线上一点的 场强。 r X xx+dx 解:建立坐标轴如图 x-x+dx电荷元产生的场强: d龙= 是d 4π6(L+r-x)
[例7-1] 均匀带电(Q)直线段延长线上一点的 场强. 建立坐标轴如图 x−x+dx电荷元产生的场强: 3.场强计算举例 X O L r x x+dx p 解: 2 0 4 ( ) Q L dx dE i L r x = + −

P点的总场强: Ejs=时 dx 4π(L+r) [讨论]若r>>L,则 龙= 点电荷的场强 4πG
2 0 0 4 ( ) Q dx L E dE i L L r x = = + − P点的总场强: 0 4 ( ) Q i r L r = + [讨论]若 r >> L,则 2 0 4 Q E i r = ——点电荷的场强
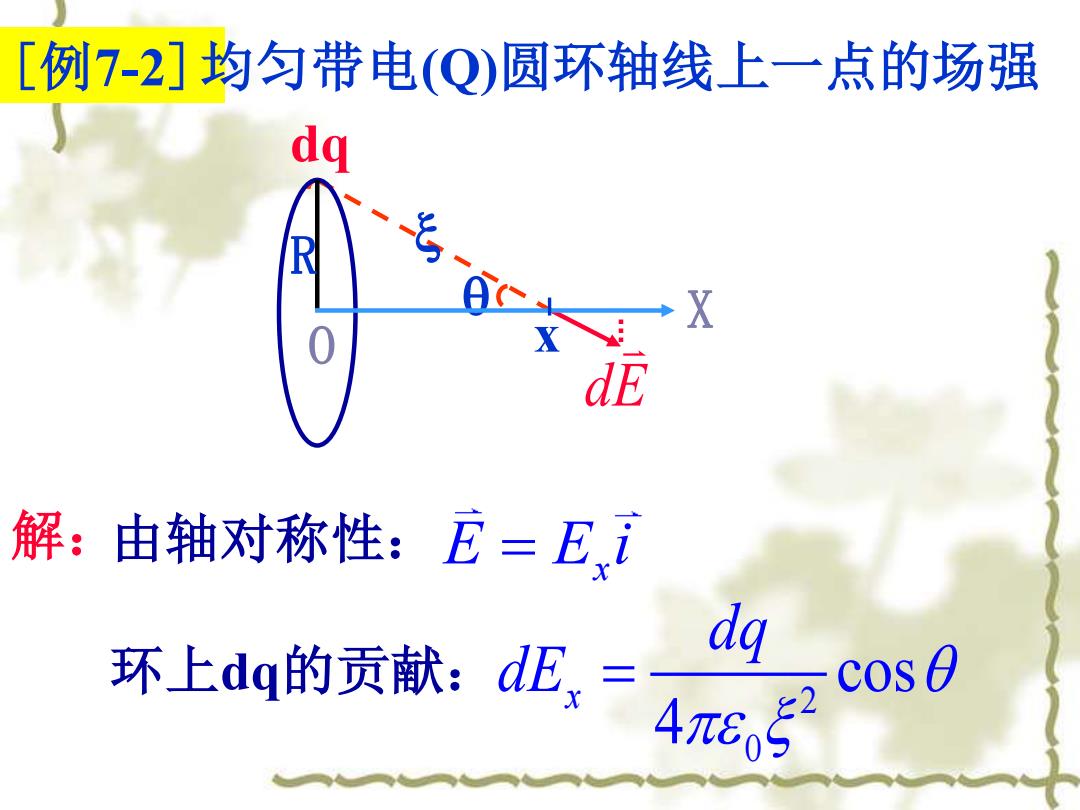
[例7-2]均匀带电(Q)圆环轴线上一点的场强 dg R dE 解:由轴对称性:E=E,i 环上dq的贡献:dE,= dq E53 cos 0
[例7-2]均匀带电(Q)圆环轴线上一点的场强 dE 由轴对称性: E E i = x 环上dq的贡献: 2 0 cos 4 x dq dE = dq 解: X O x R