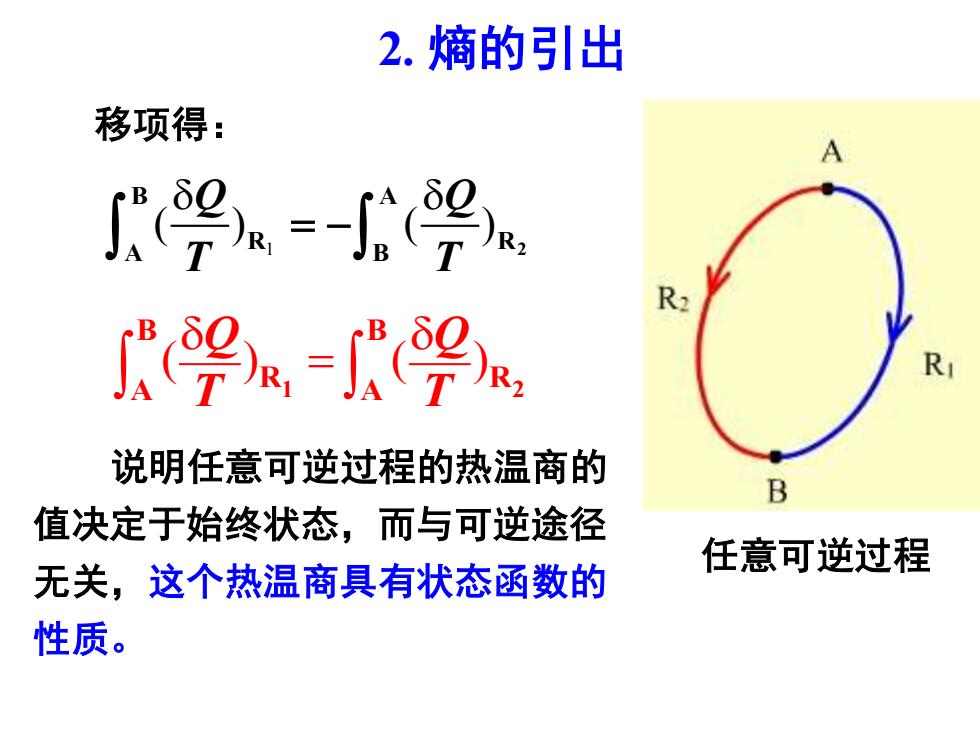
2.熵的引出 移项得: A ∫9a=-号 0 'a9e R 说明任意可逆过程的热温商的 B 值决定于始终状态,而与可逆途径 任意可逆过程 无关,这个热温商具有状态函数的 性质
2. 熵的引出 说明任意可逆过程的热温商的 值决定于始终状态,而与可逆途径 无关,这个热温商具有状态函数的 性质。 移项得: ( ) ( ) Q Q T T = 1 2 B B R R A A 任意可逆过程 1 ( ) ( ) 2 B A R R A B Q Q T T = −

2.熵的引出 Clausius根据可逆过程的热温商值决定于始终态而与 可逆过程无关这一事实定义了“熵”(entropy)这 个函数,用符号“S”表示,单位为:JK 设始、终态A,B的熵分别为SA和S,则: S。-S=心-2。 或 对微小变化 as=(9 这几个熵变的计算式习惯上称为熵的定义式, 即熵的变化值可用可逆过程的热温商值来衡量
Clausius根据可逆过程的热温商值决定于始终态而与 可逆过程无关这一事实定义了“熵”(entropy)这 个函数,用符号“S”表示,单位为: 1 J K− ( ) Q S T 对微小变化 d = R 这几个熵变的计算式习惯上称为熵的定义式, 即熵的变化值可用可逆过程的热温商值来衡量。 ( ) Q S S S T − = = B B A R A ( )i i i Q S T − = R ( )i 0 i i Q S T 或 = R 设始、终态A,B的熵分别为 SA 和 SB ,则: 2. 熵的引出

2.熵的引出 说明: (1)熵是状态函数,广度性质; (2)公式中的温度为环境温度,在可逆过程中 也是系统的温度; (3)S计算需通过可逆过程进行,但并不是只 有可逆过程才有熵变。不可逆过程的需要通过 在同样的始终态间设计可逆途径来计算
2. 熵的引出 说明: (1)熵是状态函数,广度性质; (2)公式中的温度为环境温度,在可逆过程中 也是系统的温度; (3)ΔS计算需通过可逆过程进行,但并不是只 有可逆过程才有熵变。不可逆过程的需要通过 在同样的始终态间设计可逆途径来计算

§3.5 Clausius不等式与熵增加原理 Clausius不等式 热力学第二定律的数学表达式 熵增加原理
§3.5 Clausius 不等式与熵增加原理 Clausius 不等式—— 热力学第二定律的数学表达式 熵增加原理

l.Clausius不等式 设温度相同的两个高、低温热源间有一个可逆 热机和一个不可逆热机。 则:n=+=1+ T-=1- 2 2. T T 根据Carnot定理: 7:<7R 则 2+g<0 T Th 推广为与个热源接触的任意不可逆过程,得: ②
1. Clausius 不等式 设温度相同的两个高、低温热源间有一个可逆 热机和一个不可逆热机。 T T T T T − = = − h c c R h h 1 根据Carnot定理: I R Q Q T T + c h c h 则 0 I 0 n i i i Q T < 推广为与n个热源接触的任意不可逆过程,得: h c c I h h 1 Q Q Q Q Q + 则: = = +