
特征变换 h(o) g(0) ,多分辨分解 。高分辨率图像可分解为低分辨图像+细节矩阵 ai+1 →ai →ai+l g 2di di g 。细节矩阵通过高通滤波器g()获得。 g(o)=eoh*(o+π)
多分辨分解 ◦ 高分辨率图像可分解为低分辨图像+细节矩阵 ◦ 细节矩阵通过高通滤波器g(n)获得。 h g ↑2 + ↑2 ai di h ai+1 g ai di ai+1 ↓2 ↓2 h( ) g( ) * ˆ( ) ( ) j g e h

特征变换 h(o) g(0) ,多分辨分解 。高分辨率图像可分解为低分辨图像+细节矩阵 ai+1 →ai →ai+l g 2di di g 。细节矩阵通过高通滤波器g()获得。 g(o)=eoh*(o+π)
多分辨分解 ◦ 高分辨率图像可分解为低分辨图像+细节矩阵 ◦ 细节矩阵通过高通滤波器g(n)获得。 h g ↑2 + ↑2 ai di h ai+1 g ai di ai+1 ↓2 ↓2 h( ) g( ) * ˆ( ) ( ) j g e h
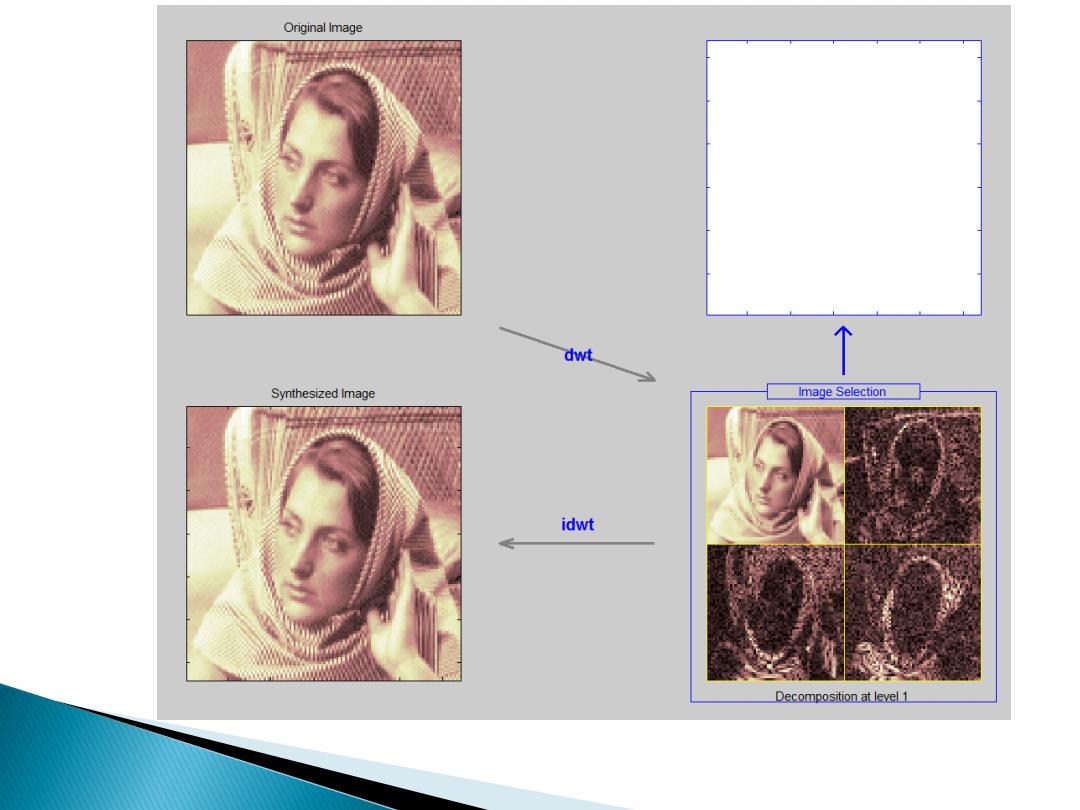
Original Image dwt Synthesized Image Image Selection idwt Decomposition at level 1
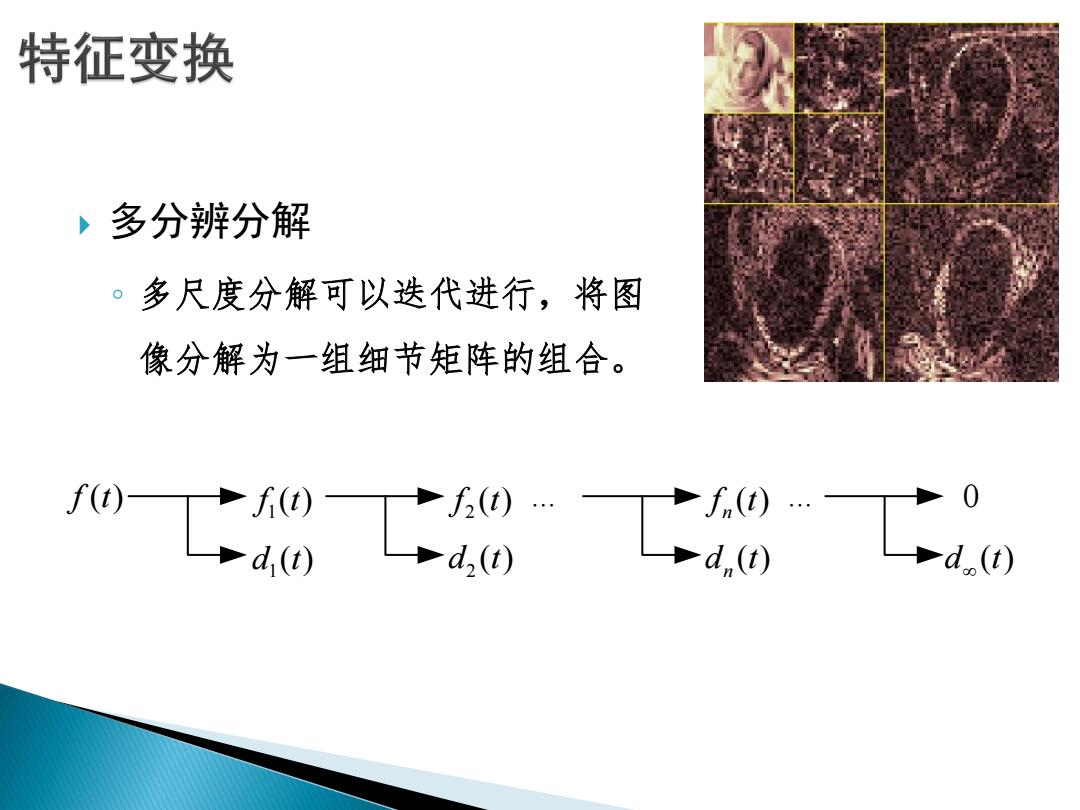
特征变换 ,多分辨分解 。多尺度分解可以迭代进行,将图 像分解为一组细节矩阵的组合。 004m9Tia
多分辨分解 ◦ 多尺度分解可以迭代进行,将图 像分解为一组细节矩阵的组合。 f t( ) 1 f t( ) 1 d t( ) 2 f t( ) 2 d t( ) ( ) n f t( ) n d t ... ... 0 d t( )

特征变换 统计方法:统计方法损失了 分析对象元素之间的序的信 息(元素之间的距离),确 知信号随机排序=随机信号, 随机信号排序=单调函数 ,统计信号分析 。对于随机变化信号,无法采用信号空间变换方法进行分 析,此时只能从中发掘其统计意义上的特征。 频谱 信号 P 200 400 500 800 700 800 900 1002003004005006007008009001000 时频谱
统计信号分析 ◦ 对于随机变化信号,无法采用信号空间变换方法进行分 析,此时只能从中发掘其统计意义上的特征。 0 100 200 300 400 500 600 700 800 900 1000 -4 -3 -2 -1 0 1 2 3 0 100 200 300 400 500 600 700 800 900 1000 0 10 20 30 40 50 60 70 80 90 2 3 4 5 6 7 8 0 5 10 15 20 25 30 35 40 45 50 Time Frequency (Hz) 信号 频谱 时频谱 统计方法:统计方法损失了 分析对象元素之间的序的信 息(元素之间的距离),确 知信号随机排序=随机信号, 随机信号排序=单调函数