
特征变换 clear all close all clc x=randn(1,1000) y fft(x) spectrogram(x,kaiser(256,5),220,512,100,'yaxis') ,统计信号分析 figure;plot(x) figure;plot(abs(y)) 。统计直方图 hist(x,200) 25 20 15 40 -2 0
统计信号分析 ◦ 统计直方图 -4 -3 -2 -1 0 1 2 3 4 0 5 10 15 20 25 clear all close all clc x = randn(1, 1000) y = fft(x) spectrogram(x,kaiser(256,5),220,512,100,'yaxis') figure; plot(x) figure; plot(abs(y)) hist(x, 200)
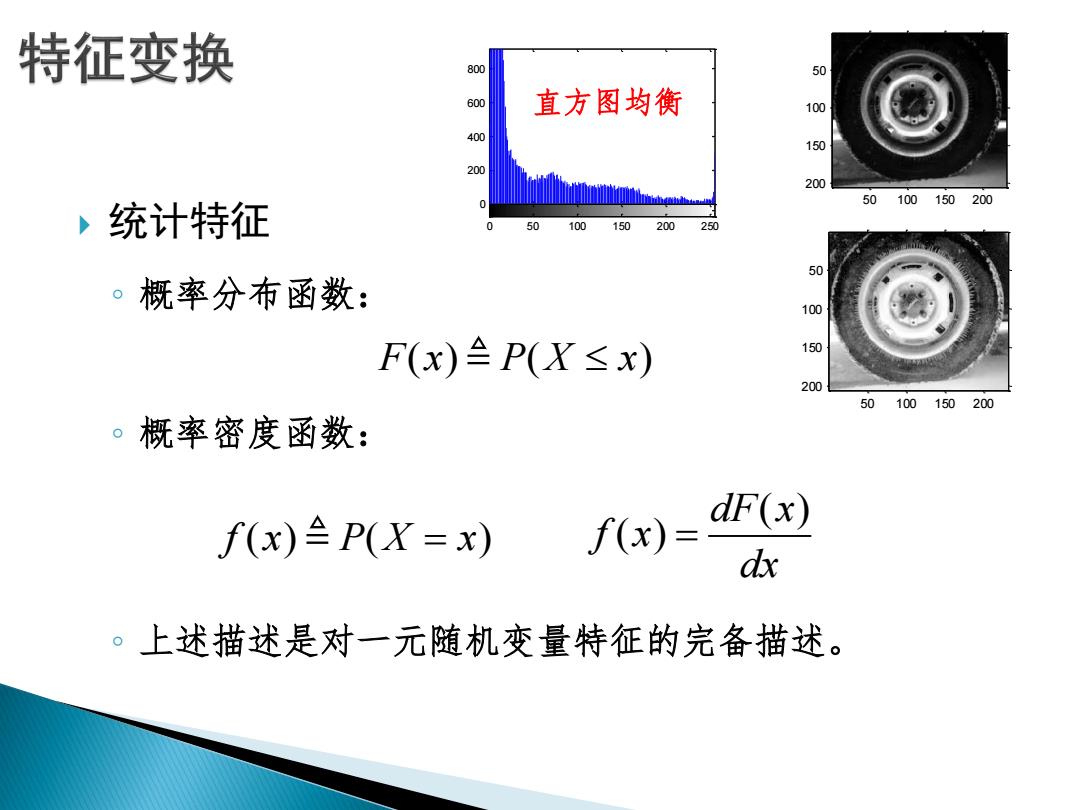
特征变换 800 50 600 直方图均衡 100 400 150 200 200 50100150200 ,统计特征 50 100 150 200 250 50 。概率分布函数: 100 F(x)≌P(X≤x) 150 200 50100150200 。概率密度函数: f(x)≌P(X=x) f(x)= dF(x) dx 。上述描述是对一元随机变量特征的完备描述
统计特征 ◦ 概率分布函数: ◦ 概率密度函数: ◦ 上述描述是对一元随机变量特征的完备描述。 f x P X x ( ) ( ) ( ) ( ) dF x f x dx F x P X x ( ) ( ) 50 100 150 200 50 100 150 200 50 100 150 200 50 100 150 200 0 200 400 600 800 0 50 100 150 200 250 直方图均衡
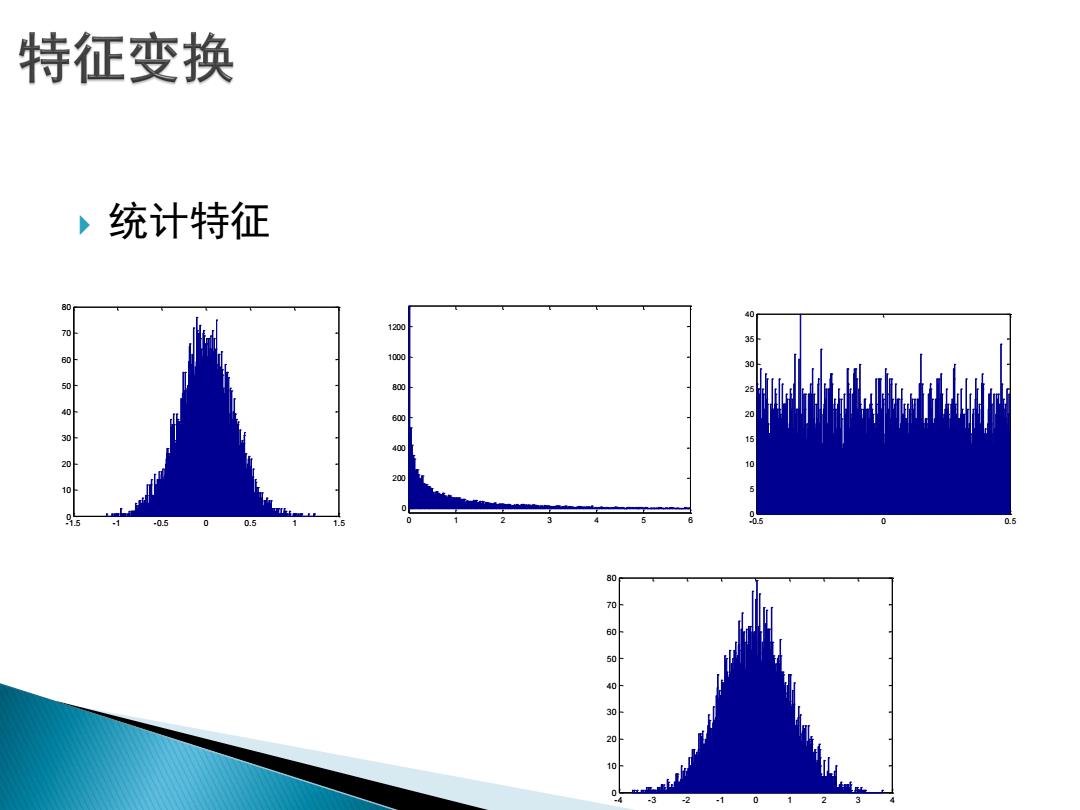
特征变换 ,统计特征 70 60 50 40 w 30 10 20 05 0.5 05 60 50 -3 -2 0 3
统计特征 -1.5 -1 -0.5 0 0.5 1 1.5 0 10 20 30 40 50 60 70 80 -4 -3 -2 -1 0 1 2 3 4 0 10 20 30 40 50 60 70 80 -0.5 0 0.5 0 5 10 15 20 25 30 35 40 0 1 2 3 4 5 6 0 200 400 600 800 1000 1200

特征变换 ,衍生函数 。特征函数(矩生成函数) ·概率密度函数的傅里叶变换 Φ(o)≌」nf(x)eora 。第二特征函数 平(o)≡lnΦ(o)
衍生函数 ◦ 特征函数(矩生成函数) 概率密度函数的傅里叶变换 ◦ 第二特征函数 ( ) ( ) j x f x e dx ( ) ln ( )

特征变换 ,统计量一一将函数参数化、指标化 。矩特征 m.=(")(x)=d"() do” 10=0 ·各阶矩相当于对特征函数的泰勒展开 ·所有阶矩可以完备表示无穷可导的PDF
统计量——将函数参数化、指标化 ◦ 矩特征 各阶矩相当于对特征函数的泰勒展开 所有阶矩可以完备表示无穷可导的PDF 0 ( ) ( ) ( ) n n n n n d m E X x f x dx d