电子科技大学：《机器学习 Machine Learning》课程教学资源（课件讲稿）第9章 Markov马尔科夫分类

马尔科夫分类 电子科技大学 师君

电子科技大学 师 君

隐马尔科夫分类 分类器训川练 系统识列

隐马尔科夫分类 分类器训练 系统识别

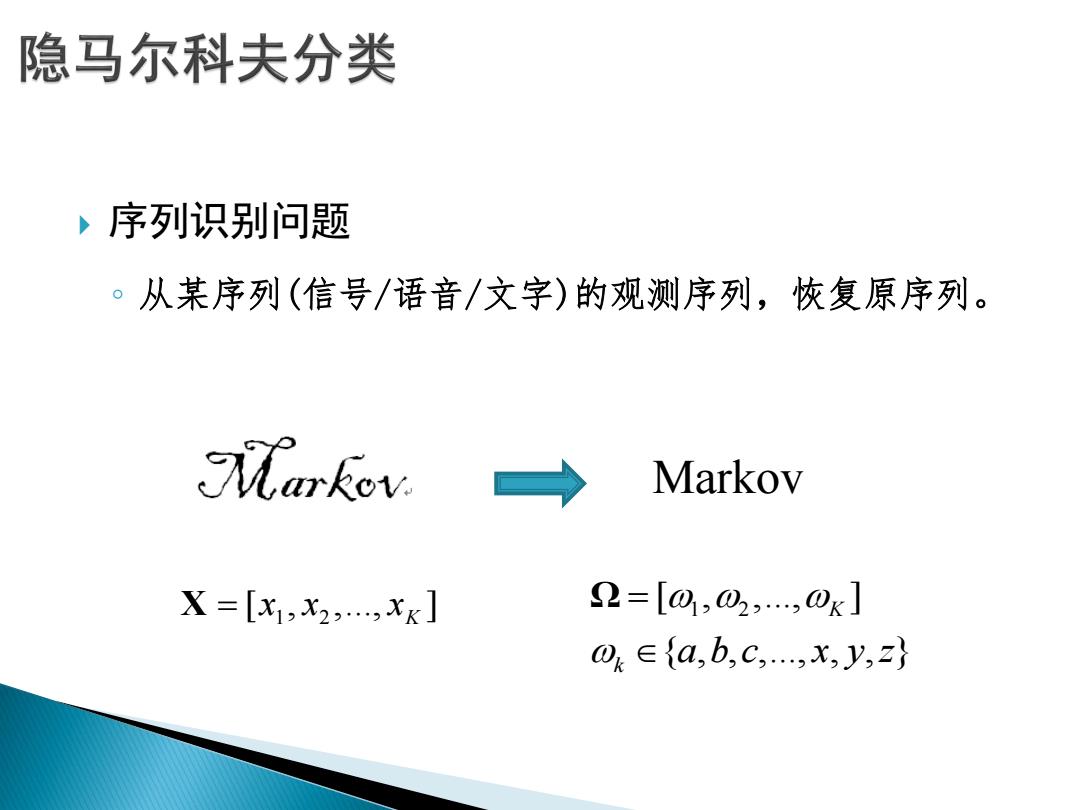
隐马尔科夫分类 ,序列识别问题 。从某序列（信号/语音/文字）的观测序列，恢复原序列。 Markov → Markov X=[X1,X2,,XK] 2=[01,02,,0k] 0∈{a,b,C,,x,y,z}

 序列识别问题 ◦ 从某序列(信号/语音/文字)的观测序列，恢复原序列。 1 2 [ , ,..., ] K X  x x x Markov 1 2 [ , ,..., ] { , , ,..., , , } K k a b c x y z       Ω

隐马尔科夫分类 ,序列识别的统计模型 。观测的独立同分布假设 ·由于噪声而产生随机性，给定状态条件下，观测量服从独 立同分布。 p(XI,)=p(xx10x) 。状态的马尔可夫假设 ·序列中某个状态出现概率与且只与其前一个状态有关。 P(0K/0K-1,,02,0）=P(0K10k-1)

 序列识别的统计模型 ◦ 观测的独立同分布假设  由于噪声而产生随机性，给定状态条件下，观测量服从独 立同分布。 ◦ 状态的马尔可夫假设  序列中某个状态出现概率与且只与其前一个状态有关。 ( / ) ( / ) i k k k p p x X Ω   1 2 1 1 ( / ,..., , ) ( / ) P P       K K K K   

隐马尔科夫分类 P(2i)=P(0k0k-1,,02,0) ,最优化模型 =P(0,)P(0k/ok-1) 。最大后验概率准则 2*=arg max(P(/X)) -agmaxP(o)P(x!P(o.)pi) k=2

 最优化模型 ◦ 最大后验概率准则 1 2 1 1 1 ( ) ( ,..., , ) ( ) ( / ) i K K k k k P P P P             Ω   1 1 1 1 2 * arg max ( / ) arg max ( ) ( / ) ( / ) ( / ) i k k k k k P P P x P p x                 Ω Ω Ω Ω X