
绘制根轨迹的基本法则 基本法测 绘制根轨迹的基本法则 法则1根轨迹的起点和终点 根轨迹起始于开环极点(×),终止于开环零点(O);如果开环零点个数 m少于开环极点个数n,则有n-m条根轨迹终止于无穷远处。 例2 G(sH(s)= s(s+2) 4口4得,4二¥4三至0Q0 第四章根轨迹法 自动控制膜理 电子信息学院11157
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 绘制根轨迹的基本法则 基本法则 绘制根轨迹的基本法则 法则 1 根轨迹的起点和终点 根轨迹起始于开环极点( ),终止于开环零点( );如果开环零点个数 m 少于开环极点个数 n,则有 n − m 条根轨迹终止于无穷远处。 例 2 G(s)H(s) = K∗ s(s + 2) j K∗ = 0 K∗ → ∞ K∗ = 0 K∗ → ∞ [s] 0 第四章 根轨迹法 自动控制原理 电子信息学院 11 / 57

绘制根轨迹的率本法则 基本法侧 绘制根轨迹的基本法则 法则2根轨迹的分支数,对称性和连续性 根轨迹的分支数=开环极点数;根轨迹连续且对称于实轴。 法则3实轴上的根轨迹 其右侧开环实零点与实极点数目之和为奇数的区域必是根轨迹。 1口。8,之¥三至)只0 第四章根轨透法 自动控制原理 电子信息学院12157
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 绘制根轨迹的基本法则 基本法则 绘制根轨迹的基本法则 法则 2 根轨迹的分支数,对称性和连续性 根轨迹的分支数 = 开环极点数 n;根轨迹连续且对称于实轴。 法则 3 实轴上的根轨迹 其右侧开环实零点与实极点数目之和为奇数的区域必是根轨迹。 j [s] 0 j 第四章 根轨迹法 自动控制原理 电子信息学院 12 / 57

绘制根轨迹的基本法则 基本法测 绘制根轨迹的基本法则 法则4新近线 ∑1P:-∑兴1马 n-m (2k+1)π n-m n>m时,n-m条根轨迹分支趋于无穷远处的规律。 口·40,立,1三,至分QC 第四章根轨迹法 自动控制膜理 电子信息学院13157
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 绘制根轨迹的基本法则 基本法则 绘制根轨迹的基本法则 法则 4 渐近线 σa = ∑n i=1 pi − ∑m j=1 zj n − m ψa = (2k + 1)π n − m n > m 时,n − m 条根轨迹分支趋于无穷远处的规律。 第四章 根轨迹法 自动控制原理 电子信息学院 13 / 57
绘制根轨迹的率本法则 基本法侧 绘制根轨迹的基本法则 例3系统开环传递函数为 G(s)= K s(s+2) 试绘制根轨迹。 解:1,实轴上的根轨迹:2,0;2,渐近 线 ∑21P%-∑名_-2+0 0a= =-1 n-m 2-0 54320 (2k+1)π ψa= =士90° n-m 123 -5 型)00 第四章根轨透法 自动控制原理 电子信息学院14157
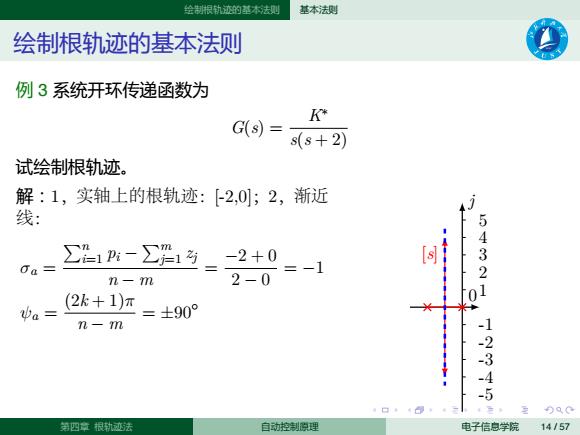
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 绘制根轨迹的基本法则 基本法则 绘制根轨迹的基本法则 例 3 系统开环传递函数为 G(s) = K∗ s(s + 2) 试绘制根轨迹。 解:1,实轴上的根轨迹:[-2,0];2,渐近 线: σa = ∑n i=1 pi − ∑m j=1 zj n − m = −2 + 0 2 − 0 = −1 ψa = (2k + 1)π n − m = ±90◦ j -5 -4 -3 -2 -1 1 2 3 4 5 [s] 0 第四章 根轨迹法 自动控制原理 电子信息学院 14 / 57

绘制根轨迹的基本法则 基本法测 绘制根轨迹的基本法则 例4单位反馈系统的开环传递函数为 G(s)= s(s+1)(s+2) 试绘制根轨迹。 解:1,实轴上的根轨迹:【-0∞-2, [-1,0;2,渐近线: 0-1-2 0a= =-1 3 a=2k+1)m =±60°,180° 3 口4二 DaG 第四章根轨迹法 自动控制膜理 电子信息学院15/57
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 绘制根轨迹的基本法则 基本法则 绘制根轨迹的基本法则 例 4 单位反馈系统的开环传递函数为 G(s) = K∗ s(s + 1)(s + 2) 试绘制根轨迹。 解:1,实轴上的根轨迹:[−∞, −2], [−1, 0];2,渐近线: σa = 0 − 1 − 2 3 = −1 ψa = (2k + 1)π 3 = ±60◦ , 180◦ j -2 -1 1 2 第四章 根轨迹法 自动控制原理 电子信息学院 15 / 57