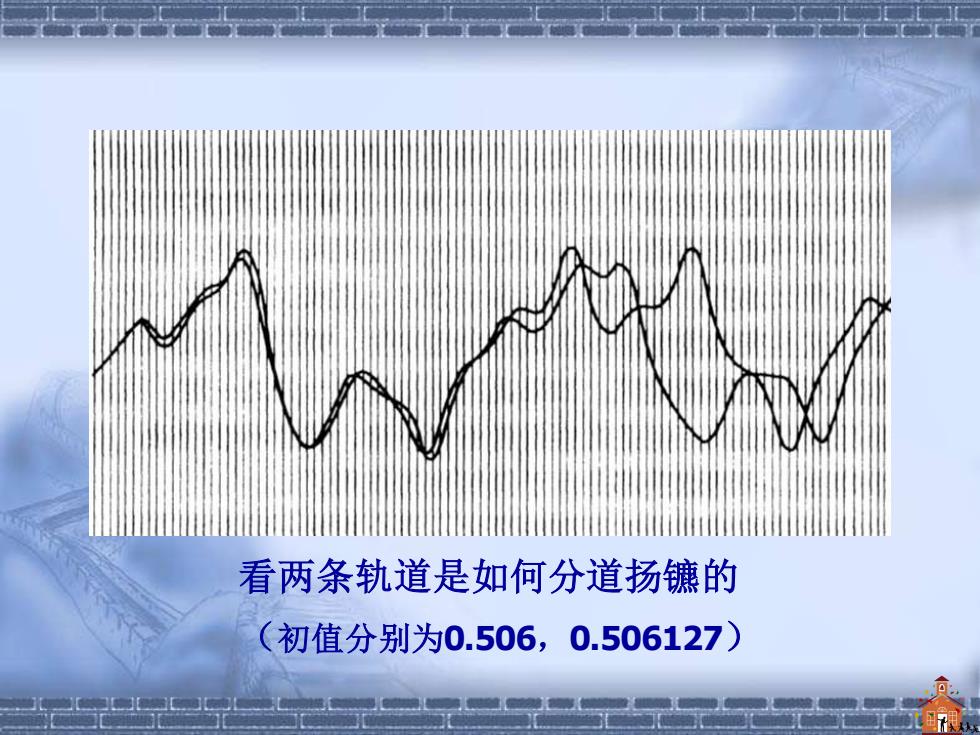
看两条轨道是如何分道扬镳的 (初值分别为0.506,0.506127)
看两条轨道是如何分道扬镳的 (初值分别为0.506,0.506127)

倍周期分岔 解释倍周期分岔现象,我们从混沌描述中最重要的的一维 非线性迭代方程式入手。这类方程中最有典型意义的是虫口方程。 x+1=Ax,(1-x) 式中的是与虫口增长率有关的控制参数,同时它的大小也 反映了系统非线性的强弱。当1<λ≤3时,不管初值是多少, 经过足够长的迭代,结果都会达到同一个确定值x。→1-1/入 这个值就叫做周期一或不动点,我们可以把这一结果想象成每 年的虫口都一样。 下一页
倍周期分岔 解释倍周期分岔现象,我们从混沌描述中最重要的的一维 非线性迭代方程式入手。这类方程中最有典型意义的是虫口方程。 (1 ) n 1 n n x = x − x + 式中的 是与虫口增长率有关的控制参数,同时它的大小也 反映了系统非线性的强弱。当 时,不管初值是多少, 经过足够长的迭代,结果都会达到同一个确定值 1 3 x →1−1/ 这个值就叫做周期一或不动点,我们可以把这一结果想象成每 年的虫口都一样。 下一页

继续增大参数入,当)>3,周期一点不再稳 定。初值稍有变化,迭代的结果就再也不会 回到周期一点1-1久,而出现了周期二。 例如: 当=33时,0.7是周期一点。现用0.669去 迭代,就会出现周期二。迭代情况如下: 无法品示该图 0.669--0.738--0.644-0.764-0.601--0.799- 0.545-0.829--0.472--0.830--0.469-0.830- 0.470--0.830-0.470. 一页
继续增大参数,当>3,周期一点不再稳 定。初值稍有变化,迭代的结果就再也不会 回到周期一点 1-1/,而出现了周期二。 例如: 当= 时,0.7是周期一点。现用0.669去 迭代,就会出现周期二。迭代情况如下: 0.669---0.738---0.644---0.764---0.601---0.799--- 0.545---0.829---0.472---0.830---0.469---0.830--- 0.470---0.830---0.470…… 3 下一页 3 1 3

现在,让参数入再增大,当=3.449时,周期二解 也变的不稳定了,取而代之的是稳定的周期四解。当 参数继续增大,使得λ=3.544时,周期四解又变的不稳 定了,取而代之的是稳定的周期八解。一直迭代下去, 还会出现周期十六、周期三十二等等。这就是著名的 倍周期分岔现象。 值得注意的是,周期倍增过程没有限制,可以一 直这样分下去,但对应的入值却有一个极限入。,到达 入。时,迭代的稳定解是2∞周期解--周期无穷大,也就 是没有周期。所以这时得到的是非周期解,迭代的数 据到处乱跑,无法把握,系统进入混沌状态。 倍周期分岔产生的混沌,在心脏生理学方面有潜 在的应用价值。心律不齐,心肌梗塞这些医学难题, 有可能找到正确的答案。 下一页
现在,让参数再增大,当=3.449时,周期二解 也变的不稳定了,取而代之的是稳定的周期四解。当 参数继续增大,使得=3.544时,周期四解又变的不稳 定了,取而代之的是稳定的周期八解。一直迭代下去, 还会出现周期十六、周期三十二等等。这就是著名的 倍周期分岔现象。 值得注意的是,周期倍增过程没有限制,可以一 直这样分下去,但对应的值却有一个极限, ,到达 , 时,迭代的稳定解是2 周期解---周期无穷大,也就 是没有周期。所以这时得到的是非周期解,迭代的数 据到处乱跑,无法把握,系统进入混沌状态。 倍周期分岔产生的混沌,在心脏生理学方面有潜 在的应用价值。心律不齐,心肌梗塞这些医学难题, 有可能找到正确的答案。 下一页

SP 3P 6P 2P 2.92401 3.92 倍周期分岔图
倍周期分岔图