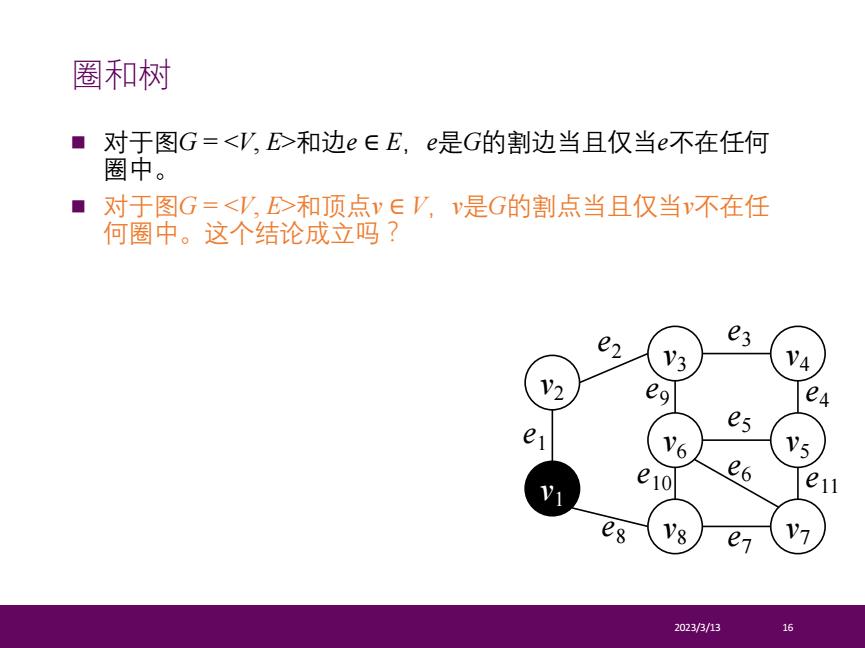
圈和树 ■对于图G=<V,E>和边e∈E,e是G的割边当且仅当e不在任何 圈中。 ■ 对于图G=<V,>和顶点v∈V,v是G的割点当且仅当v不在任 何圈中。这个结论成立吗? e2 e3 '3 V4 V2 eg es e10 e6 e e8 V7 2023/3/13 16
n 对于图G = <V, E>和边e ∈ E,e是G的割边当且仅当e不在任何 圈中。 n 对于图G = <V, E>和顶点v ∈ V,v是G的割点当且仅当v不在任 何圈中。这个结论成立吗? 2023/3/13 16 圈和树 v1 e1 v2 v3 v6 v8 v4 v5 v7 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11

圈和树 ■树:不含圈的连通图 V5 y 内 '3 2023/3/13 17
n 树:不含圈的连通图 2023/3/13 17 圈和树 v1 v2 v3 v4 v5
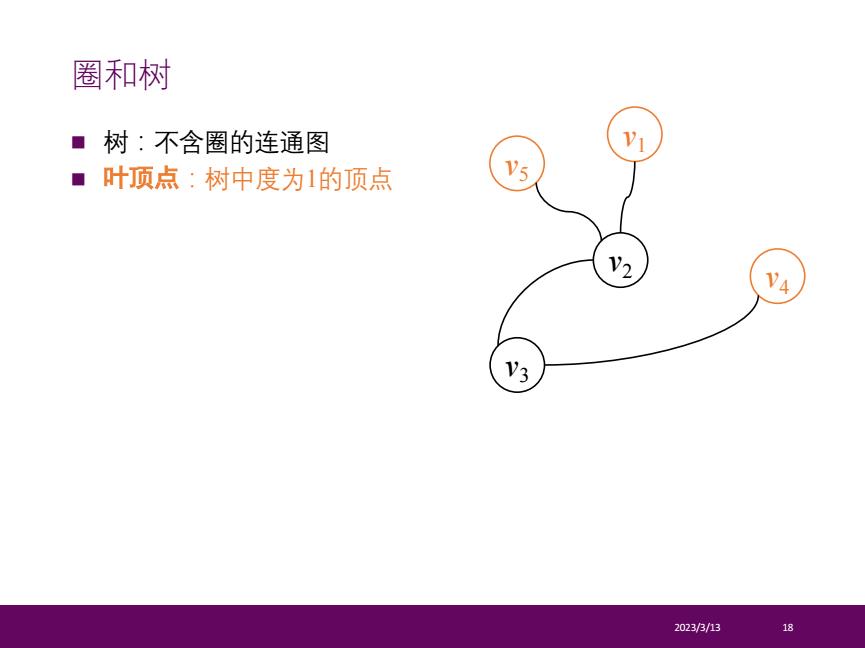
圈和树 ■树:不含圈的连通图 ■叶顶点:树中度为1的顶点 2 3 2023/3/13 18
n 树:不含圈的连通图 n 叶顶点:树中度为1的顶点 2023/3/13 18 圈和树 v1 v2 v3 v4 v5
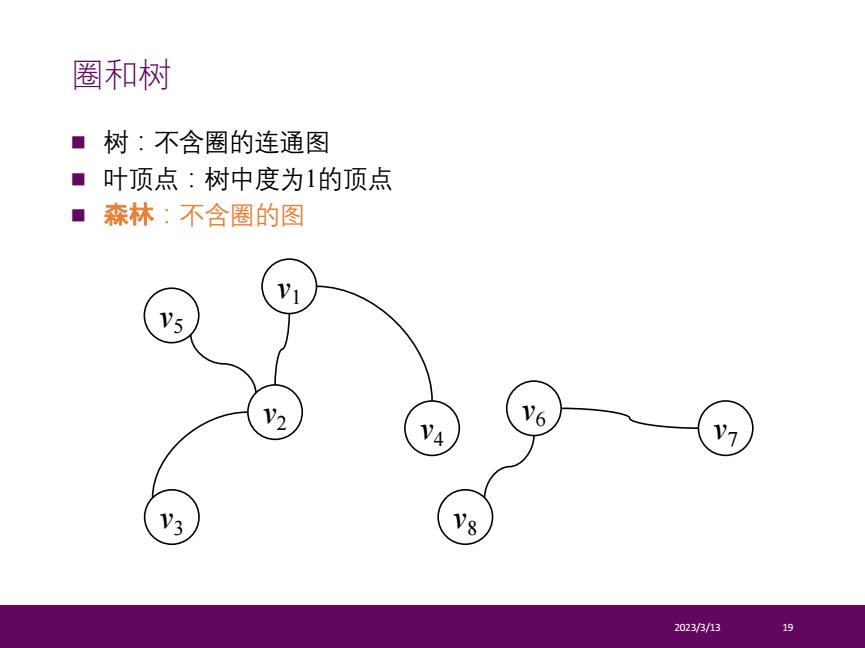
圈和树 ■树:不含圈的连通图 ■叶顶点:树中度为1的顶点 ■森林:不含圈的图 V5 V4 V6 V 小) V8 2023/3/13 9
n 树:不含圈的连通图 n 叶顶点:树中度为1的顶点 n 森林:不含圈的图 2023/3/13 19 圈和树 v6 v8 v7 v1 v2 v3 v4 v5

圈和树 ■树的等价定义: ●图G连通且不含圈。 ·图G中任意两个顶点间有且只有一条路。 ●图G不含圈且(G=WG-1。 ●图G连通且(G=v(G-1。 ●图G极小连通,即:G连通,但删除任意一条边均不连通。 ·图G极大无圈,即:G不含圈,但增加任意一条边均形成圈。 2023/3/13 20
n 树的等价定义: l 图G连通且不含圈。 l 图G中任意两个顶点间有且只有一条路。 l 图G不含圈且ε(G) = ν(G) – 1。 l 图G连通且ε(G) = ν(G) – 1。 l 图G极小连通,即:G连通,但删除任意一条边均不连通。 l 图G极大无圈,即:G不含圈,但增加任意一条边均形成圈。 2023/3/13 20 圈和树