解 两种假设下的似然函数为 f(zIH)= (21-A)2 2σ2 A(z)= ep( 1 对数似然比为 N InA(z)= NA N 判决表达式为 1 Zi 24) Inno i= Ho
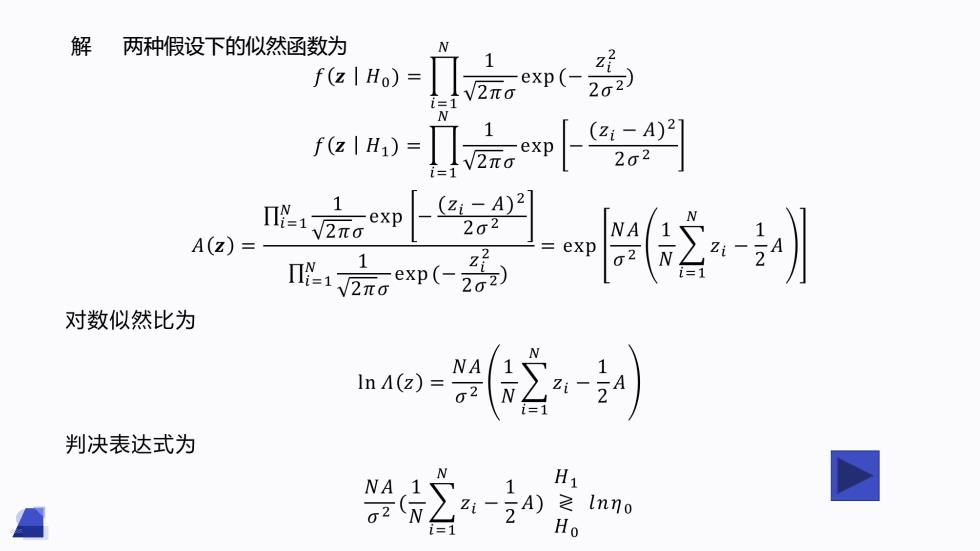
解 两种假设下的似然函数为

Ha ainno 令z=∑Y121,将上式整理后得z NA IA=Y Ho 检验统计量z为样本均值,为了确定判决的性能,首先需要确定检验统计量的分布,在H。 为真时,到Ho=1v,那么 在H1为真时,Z到H1=别1A+)=A+∑1i,那么 fz(ZH)=-

所以,虚警概率为 P,=P>yIH)=“2mep(-)a=Q(-) (9.2.7) 检测概率为 P=P(z>rH,)=xp(←号)dz=Qg(9.28) 当采用最小错误概率准则且P(H1)=P(H)=1时,判决表达式为

H11 Ho P,=().=()-=1-) 总的错误概率为 R=PH,P,+Pm,Pw=0() 例9.3 设两种假设下的观测为 Ho:zi~N(0,0o) (i=1,2,…,N,02>0) H1:z1~N(0,o) 求判决表达式,并确定判决性能。 解先计算似然比:

I 1 一exp(- 1 A(z)= 2a) -12π0 1 exp(- 1 z) 2 06 对数似然比为 In A(z)=NIn(co/a;)+ 品 判决表达式为对数似然比和对数门限进行比较,经化简后得 z H。-6 2[lnno NIn(01/0o)]=Y