DE在平面ABC内,因此A、B、C、D、E五点在同一平面内。所以这五点中的任意两点连线 都在平面ABC内。此外本题利用了点在直线上,该点的投影必在该直线的投影上这个特性。 解题步骤: 1.连接点A和点D的正面投影a'和d',直线a'd'与直线b'c'交于点G的正面投影g' 由于点G在直线C上,因此点G的水平投影g必在直线BC的水平投影bC上,从g'直接作竖 直辅助线交于bC得到点G的水平投影g。点G在直线D上,因此其水平投影g在直线水平投 影ad上。过点A和点G的水平投影a和g作一条直线并延长,从点D的正面投影d'作竖直辅 助线与直线ag交于点D的水平投影d。 2.连接点A和点E的正面投影a'和e',直线a'e'与直线b'c'交于点F的正面投影f' 由于点F在直线C上,因此点F的水平投影f必在直线BC的水平投影bc上,从f'直接作竖 直辅助线得到点F的水平投影f。点F在直线AE上,因此其水平投影f在直线水平投影ae上。 过点A和点F的水平投影a和f作一条直线,从点E的正面投影e'作竖直辅助线与直线af交 于点E的水平投影e。 3.连接d和e并加粗,得到直线DE的水平投影,参见图1.3(b)。 b 图13 例4下图为被截切的立方体,试分析图中直线AB、直线C、直线DE、直线CE、直线AD、直线 D、直线GR、直线GA及平面ABC、平面DEF、平面ADF、平面GAB的类型。(参见图1,4(a)。 解题分析:本题目主要考查不同直线以及不同平面的类型。利用各自的特性来分析。结合点 线面的投影对应关系和线面的空间位置进行解题。 解题步骤: 1.根据已有视图以及点A、B、C、D、E、F的正面投影a'、b'、c'、c'、e'、f'作出 这六个点的水平投影和侧面投影,参见图1.4(b)
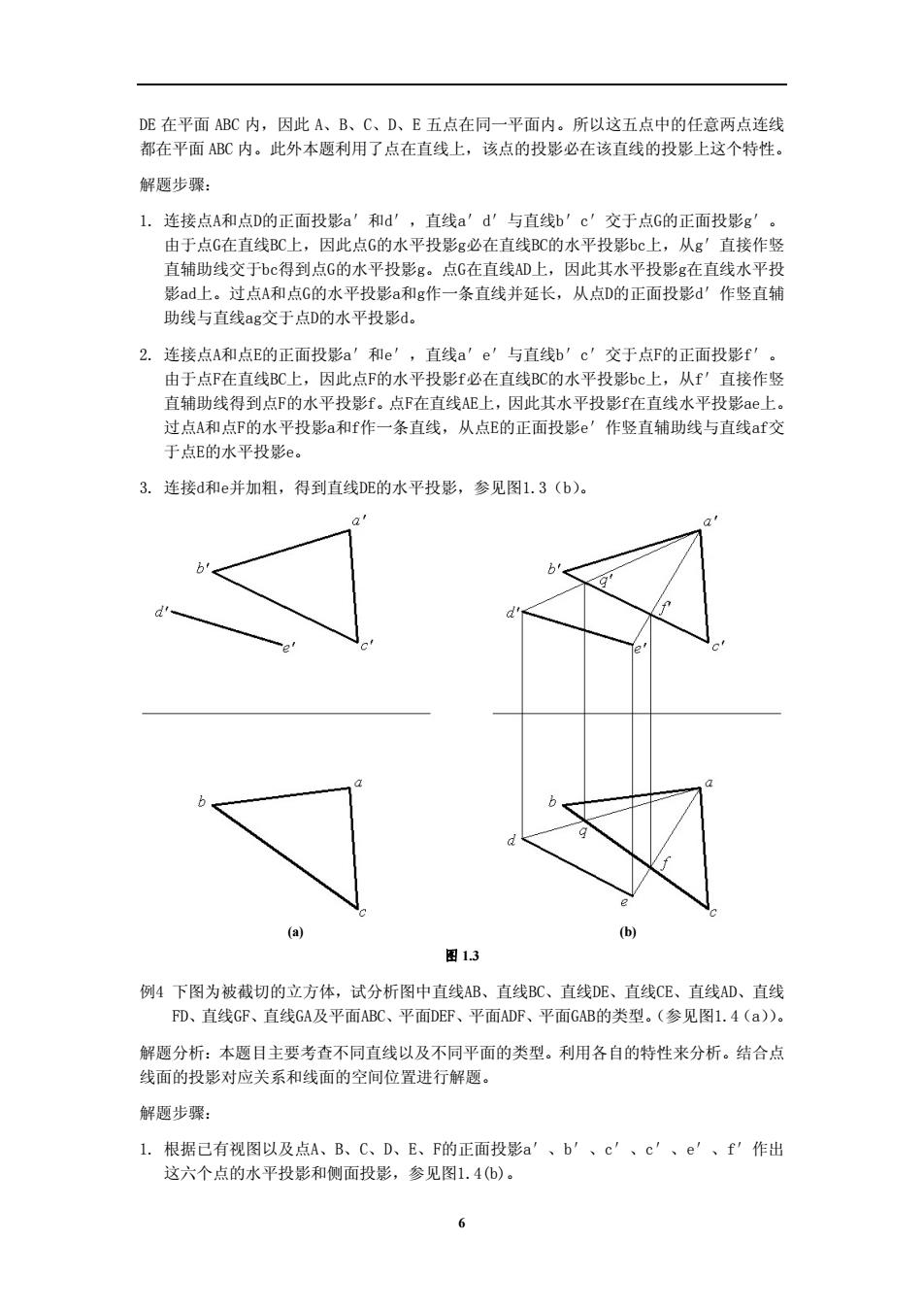
DE 在平面 ABC 内,因此 A、B、C、D、E 五点在同一平面内。所以这五点中的任意两点连线 都在平面 ABC 内。此外本题利用了点在直线上,该点的投影必在该直线的投影上这个特性。 解题步骤: 1. 连接点A和点D的正面投影a′和d′,直线a′d′与直线b′c′交于点G的正面投影g′。 由于点G在直线BC上,因此点G的水平投影g必在直线BC的水平投影bc上,从g′直接作竖 直辅助线交于bc得到点G的水平投影g。点G在直线AD上,因此其水平投影g在直线水平投 影ad上。过点A和点G的水平投影a和g作一条直线并延长,从点D的正面投影d′作竖直辅 助线与直线ag交于点D的水平投影d。 2. 连接点A和点E的正面投影a′和e′,直线a′e′与直线b′c′交于点F的正面投影f′。 由于点F在直线BC上,因此点F的水平投影f必在直线BC的水平投影bc上,从f′直接作竖 直辅助线得到点F的水平投影f。点F在直线AE上,因此其水平投影f在直线水平投影ae上。 过点A和点F的水平投影a和f作一条直线,从点E的正面投影e′作竖直辅助线与直线af交 于点E的水平投影e。 3. 连接d和e并加粗,得到直线DE的水平投影,参见图1.3(b)。 (a) (b) 图 1.3 例4 下图为被截切的立方体,试分析图中直线AB、直线BC、直线DE、直线CE、直线AD、直线 FD、直线GF、直线GA及平面ABC、平面DEF、平面ADF、平面GAB的类型。(参见图1.4(a))。 解题分析:本题目主要考查不同直线以及不同平面的类型。利用各自的特性来分析。结合点 线面的投影对应关系和线面的空间位置进行解题。 解题步骤: 1. 根据已有视图以及点A、B、C、D、E、F的正面投影a′、b′、c′、c′、e′、f′作出 这六个点的水平投影和侧面投影,参见图1.4(b)。 6

2.直线AB的水平投影b平行于X轴,其侧面投影a”c”平行于Z轴。可以分析出直线B平行 于正面,倾斜于水平面和侧面,因此为正平线。直线C的水平投影红平行于X轴,其正面 侧面投影”c”积聚为一点。由此可以分析出直线BC垂直于侧 平行于水平面和正面,因此为侧垂线。直线DE的水平投影de平行于X轴, 其正面投 d'e'平行于X轴,侧面投影d”e”积聚为一点。由此可以分析出直线DE垂直于侧面 平行于水平面和正面,因此为侧垂线。直线CE的水平投影ce积聚为一点,它的正面投影 c'e'平行于Z轴,侧面投影c”e”平行于Z轴。由此可以分析出直线CE垂直于水平面, 平行于正面和侧面,因此为铅垂线。直线D的水平投影d积聚为一点,它的正面投影 d'平行于Z轴, 侧面投影a”d”平行于z轴, 由此可以分析出直线AD垂直于水平面 平行于正面和侧面,因此为铅垂线。直线D的正面投影f'd'积聚为 一点,它的水平投 影f平行于Y轴,侧面投影f”d”平行于Y轴。由此可以分析出直线FD垂直于正面,平行 于水平面和侧面,因此为正垂线。直线GF的水平投影g积聚为一点,它的正面投影gf平 行于轴,侧面投影g””平行于?轴。由此可以分析出直线GF垂直于水平面,平行于正 面和侧面,因此为铅垂线。直线GA的正面投影g'a'积聚为一点,它的水平投影ga平行 于Y轴,侧面投影g”a”平行于Y轴。由此可以分析出直线GA垂直于正面,平行于水平面 和侧面,因此为正垂线。 3.平面BC的水平投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线,而 且平行于Z轴,由此可以分析出平面BC与正面平行,与水平面和侧面垂直,所以为正平 面。平面DF的正面投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线, 而且平行于Y轴,由此可以分析出平面与水平面平行,与正面和侧面垂直,因此为水 平面。平面ADF的水平投影积聚为一条直线,而且平行于Y轴,其正面投影积聚为一条直 线,而且平行于Z轴,由此可以分析出平面ADF与侧面平行,与水平面和正面垂直,所以 为侧平面。平面GAB的正面投影积聚为一条倾斜直线,其水平面投影为gab,侧面投影为 a”b”。由此可以分析出平面GAB垂直于正面,倾斜于水平面和正面,所以为正垂面 图1d 1.5.2习题及答案 习题1已知点A在点B之前4毫米,之上10毫米,之右8毫米,求A点的投影(参见图1.5 (a). 解题分析:从己知图中可以看出点B的三面投影是已知的,需要根据点A和点B之间的空间 位置关系来确定点A的投影。此题主要通过两点之间的相对位置来进行解题。 >
2. 直线AB的水平投影ab平行于X轴,其侧面投影a〞c〞平行于Z轴。可以分析出直线AB平行 于正面,倾斜于水平面和侧面,因此为正平线。直线BC的水平投影bc平行于X轴,其正面 投影b′c′平行于X轴, 侧面投影b〞c〞积聚为一点。由此可以分析出直线BC垂直于侧 面,平行于水平面和正面,因此为侧垂线。直线DE的水平投影de平行于X轴,其正面投影 d′e′平行于X轴, 侧面投影d〞e〞积聚为一点。由此可以分析出直线DE垂直于侧面, 平行于水平面和正面,因此为侧垂线。直线CE的水平投影ce积聚为一点,它的正面投影 c′e′平行于Z轴, 侧面投影c〞e〞平行于Z轴。由此可以分析出直线CE垂直于水平面, 平行于正面和侧面,因此为铅垂线。直线AD的水平投影ad积聚为一点,它的正面投影 a′d′平行于Z轴, 侧面投影a〞d〞平行于Z轴。由此可以分析出直线AD垂直于水平面, 平行于正面和侧面,因此为铅垂线。直线FD的正面投影f′d′积聚为一点,它的水平投 影fd平行于Y轴, 侧面投影f〞d〞平行于Y轴。由此可以分析出直线FD垂直于正面,平行 于水平面和侧面,因此为正垂线。直线GF的水平投影gf积聚为一点,它的正面投影gf平 行于Z轴, 侧面投影g〞f〞平行于Z轴。由此可以分析出直线GF垂直于水平面,平行于正 面和侧面,因此为铅垂线。直线GA的正面投影g′a′积聚为一点,它的水平投影ga平行 于Y轴, 侧面投影g〞a〞平行于Y轴。由此可以分析出直线GA垂直于正面,平行于水平面 和侧面,因此为正垂线。 3. 平面ABC的水平投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线,而 且平行于Z轴,由此可以分析出平面ABC与正面平行,与水平面和侧面垂直,所以为正平 面。平面DEF的正面投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线, 而且平行于Y轴,由此可以分析出平面DEF与水平面平行,与正面和侧面垂直,因此为水 平面。平面ADF的水平投影积聚为一条直线,而且平行于Y轴,其正面投影积聚为一条直 线,而且平行于Z轴,由此可以分析出平面ADF与侧面平行,与水平面和正面垂直,所以 为侧平面。平面GAB的正面投影积聚为一条倾斜直线,其水平面投影为gab,侧面投影为 g〞a〞b〞。由此可以分析出平面GAB垂直于正面,倾斜于水平面和正面,所以为正垂面。 (a) (b) 图 1.4 1.5.2 习题及答案 习题 1 已知点 A 在点 B 之前 4 毫米,之上 10 毫米,之右 8 毫米,求 A 点的投影(参见图 1.5 (a))。 解题分析:从已知图中可以看出点 B 的三面投影是已知的,需要根据点 A 和点 B 之间的空间 位置关系来确定点 A 的投影。此题主要通过两点之间的相对位置来进行解题。 7