
10.1谐振动 谐振动的特征: (1)合外力为线性回复力F=-k (2)加速度与位移成正比且反向 dt2 =-02x (3)位移是时间的余弦函数x=Ac0s(ot+) 简谐振动的速度 速度最大值 v=dr =-@Asin(@t+o) Um =@A dt 简谐振动的加速度 加速度最大值 d2x Q= dr2 =-02Ac0s(ot+4) 0m=02A 前页后页目录 6
前页 后页 目录 6 10.1 谐振动 谐振动的特征: (1)合外力为线性回复力 (2)加速度与位移成正比且反向 F kx x = − 2 2 2 d d x x t = − (3)位移是时间的余弦函数 0 x A t = + cos( ) 简谐振动的速度 d d x t v = 0 = − + A t sin( ) 简谐振动的加速度 2 2 d d x a t = 2 0 = − + A t cos( ) vm =A 2 a A m = 加速度最大值 速度最大值

10.1谐振动 二.描述谐振动的特征量 x=Acos(at+) 1)振幅4 SI制:m(米) 质点离开平衡位置的最大位移的绝对值。 2)周期T SI制:s(秒) 完成一次完整振动所经历的时间。 x=Acos(@t+)=Acos[@(T+t)+] oT=2元 T=2n 0 前页后页目录7
前页 后页 目录 7 10.1 谐振动 1)振幅A 2)周期T 0 x A t = + cos( ) 0 = + + A T t cos[ ( ) ] T = 2π 2π T = A A o x 二. 描述谐振动的特征量 0 x A t = + cos( ) 质点离开平衡位置的最大位移的绝对值。 SI制:m(米) 完成一次完整振动所经历的时间。 SI制:s(秒)

10.1谐振动 3)频率y SI制:Hz(赫兹) 单位时间内完成的完整振动的次数。 10 T2π 4圆频率0 SI制:rad/s(孤度/秒) 2π单位时间内完成的完整振动的次数。 2π 0=2πy= 前页后页目录 8
前页 后页 目录 8 10.1 谐振动 3)频率n 1 T n = 2π = 4)圆频率 n = 2π 单位时间内完成的完整振动的次数。 SI制:Hz(赫兹) 2单位时间内完成的完整振动的次数。 SI制:rad/s(弧度/秒) 2π T =

10.1谐振动 简谐振动表达式 x=Acos(@t+) 2 x=Acos t+% x=Ac0s(2πvt+4) 5)相位中 0t+央-2开1+质=2m1t负 决定简谐振动质点的运动状态。 初相 t=0时刻的相位。 前页后页目录 9
前页 后页 目录 9 10.1 谐振动 简谐振动表达式 5)相位 0 = +t 初相0 0 x A t = + cos( ) 0 2π x A t cos T = + x A t = + cos(2πn 0 ) 0 2π t T = + 0 = + 2πn t 决定简谐振动质点的运动状态。 t =0时刻的相位
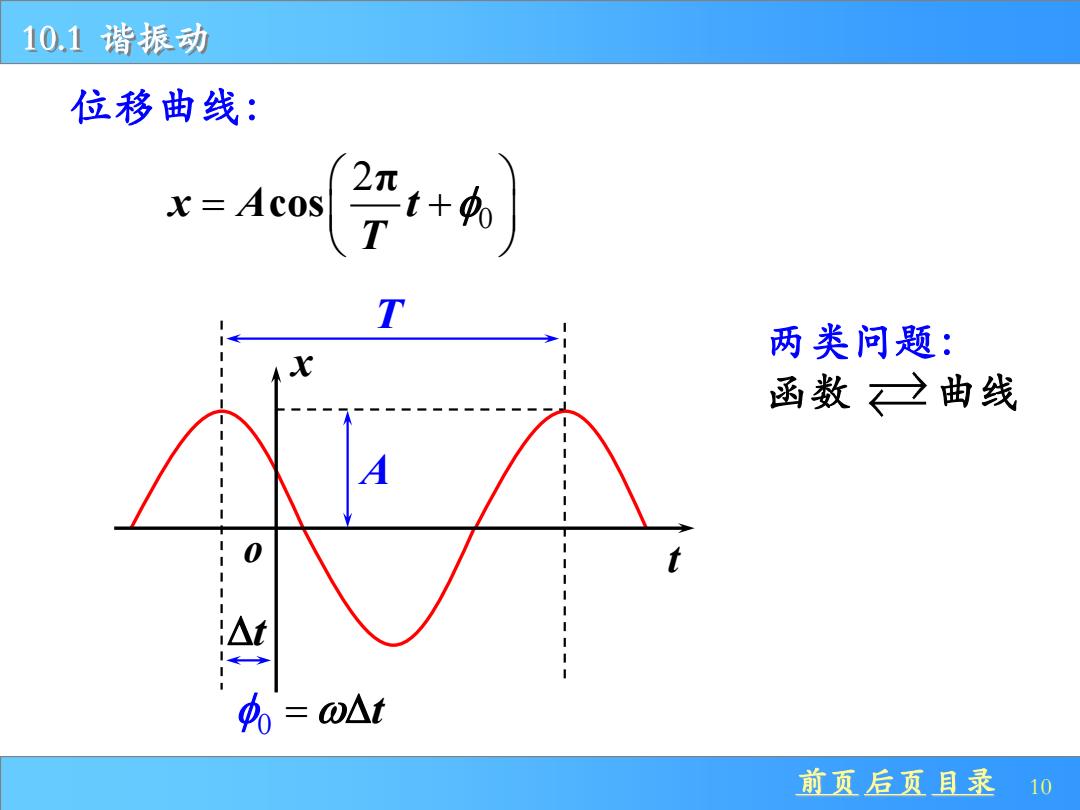
10.1谐振动 位移曲线: x=Acos 2 -t+o 两类问题: 函数之曲线 %=0△t 前页后页目录10
前页 后页 目录 10 10.1 谐振动 位移曲线: A o x t T 0 =t t 两类问题: 函数 曲线 0 2π x A t cos T = +