
(20-8) 等价于 2=,=1 (20-9) 可以证明,在H。成立的条件下,如果样本量较大,Z近似地服从标准正态分布N(0,), x2近似地服从自由度为1的x2分布。 2.回归系数的区间估计 己知b的抽样分布近似地服从正态分布,根据正态分布理论,总体回归系数B的(1-α) 置信区间为b±Z.12S。,则OR的估计值为e,(I-a)置信区间为 e(bZanS,) (20-10) 3.实例:假设检验和参数估计(基于SAS的输出) (1)关于模型的似然比检验 模型中仅有常数项(回归系数B=0)时,nL。=6413.618,加入自变量X后, hL,=6150.751,似然比统计量 G=2nL1-nL)=2(-6150.751)-(-6413.618)=525.733 P<0.0001,拒绝H。,可以认为所建立的ogistic回归方程是有意义的。 (2)关于参数的Wa1d检验及OR的置信区间 表20-2参数估计、Wald检验和OR 变量参数估计值 OR95%置信区 S。Waldx2P值 OR 名 b 间 常数 -1.41170.03062132.7414<0.0001 项 X1.00300.0440518.6950<0.00012.7272.501-2.972 由表20-2,b。=-1.4117,b=1.0030,可以立即写出l0 gistic回归方程 =-147+100x
Sb b Z − 0 = (20-8) 等价于 2 2 ( ) Sb b = , =1 (20-9) 可以证明,在 H0 成立的条件下,如果样本量较大, Z 近似地服从标准正态分布 N(0,1) , 2 近似地服从自由度为 1 的 2 分布。 2. 回归系数的区间估计 已知 b 的抽样分布近似地服从正态分布,根据正态分布理论,总体回归系数 的 (1−) 置信区间为 b Z / 2 Sb ,则 OR 的估计值为 b e ,(1−) 置信区间为 ( ) b Z / 2 Sb e (20-10) 3.实例:假设检验和参数估计(基于SAS的输出) (1)关于模型的似然比检验 模型中仅有常数项(回归系数 = 0 )时, ln L0 = −6413.618 ,加入自变量 X 后, ln L1 = −6150.751,似然比统计量 G = 2(ln L1 − ln L0 ) = 2[(−6150.751) − (−6413.618)] = 525.733 P <0.0001,拒绝 H0 ,可以认为所建立的 logistic 回归方程是有意义的。 (2)关于参数的Wald检验及 OR 的置信区间 表20-2 参数估计、Wald检验和 OR 变量 名 参数估计值 b b S Wald 2 P 值 OR OR 95%置信区 间 常数 项 -1.4117 0.0306 2132.7414 <0.0001 X 1.0030 0.0440 518.6950 <0.0001 2.727 2.501~2.972 由表 20-2,b0 = −1.4117 ,b =1.0030 ,可以立即写出 logistic 回归方程 X p p ) 1.4117 1.0030 1 ln( = − + −

e-1411741.0030x) p=1+e-14mLo0西 左端我们写的是P而不是π,这是因为右端的系数是,和b,而不是B。和B,表明这里 的Logistic回归方程是根据样本资料对理论模型的估计。 对单个回归系数进行Wald检验,Wald统计量x2=518.6950,P<0.0001,可以认为 超重或晒胖对高血压病有影响。OR估计值为 0R=e5=e00=2.727 OR的95%置信区间为 e(bZun:s。)=e0030t196040=2s01,297m 这个置信区间并不包含1,上下限均大于1,再次表明,超重或肥胖是高血压病的危险因素, 4.实例:自变量筛选(基于SAS的输出) 例202为研究居民两周患病未治疗的影响因素,采用多阶段分层整群抽样,对某地 1790名农村居民进行了入户调查。调查内容包括性别(男0,女:1)、年龄(<5岁:1,5 岁2,15岁3,45岁-4,65岁5)、年人均收入(不低于平均水平0,低于平均水平1)、 医疗保障(有:0,无:1)、距就近医疗点时间(<10分钟:1,10分钟2,30分钟3)、自 感疾病严重程度(不严重:1,一般:2,严重3)、发病时间(急性病两周内发生:1,急性病 两周前发生延续到两周内2,慢性病持续到两周内:3、就诊(就诊:0,未就诊1)。11790 名居民中,调查前二周患病者1649人,其中未就医者720人,患者有关资料整理结果见表 20-3. 表20-3某地二周患病者门诊医疗卫生服务利用影响因素资料 忠者性别年龄年人均收入医疗保障 距就近医自感疾病发病 就诊 疗点时间严重程度时间 编号 X X2 X X。X, y 1 1 ¥ 0 2 3 0
或 ( 1.4117 1.0030 ) ( 1.4117 1.0030 ) 1 X X e e p − + − + + = 左端我们写的是 p 而不是 ,这是因为右端的系数是 0 b 和 1 b ,而不是 0 和 1 ,表明这里 的 Logistic 回归方程是根据样本资料对理论模型的估计。 对单个回归系数进行 Wald 检验, Wald 统计量 2 =518.6950,P <0.0001, 可以认为, 超重或肥胖对高血压病有影响。OR 估计值为 2.727 ˆ 1.0030 OR = e = e = b OR 的 95%置信区间为 = = ( ) (1.00301.960.0440) / 2 e e b Z Sb (2.501, 2.972) 这个置信区间并不包含 1,上下限均大于 1,再次表明,超重或肥胖是高血压病的危险因素。 4.实例:自变量筛选(基于SAS的输出) 例 20-2 为研究居民两周患病未治疗的影响因素,采用多阶段分层整群抽样,对某地 11790 名农村居民进行了入户调查。调查内容包括性别(男:0 ,女:1)、年龄(<5 岁:1,5 岁-:2,15 岁-:3 ,45 岁-:4 ,65 岁-:5 )、年人均收入(不低于平均水平:0,低于平均水平:1)、 医疗保障(有:0 ,无:1)、距就近医疗点时间(<10 分钟:1,10 分钟-:2,30 分钟-:3) 、自 感疾病严重程度(不严重:1,一般:2,严重:3)、发病时间(急性病两周内发生:1,急性病 两周前发生延续到两周内:2,慢性病持续到两周内:3)、就诊(就诊:0,未就诊:1)。11790 名居民中,调查前二周患病者 1649 人,其中未就医者 720 人,患者有关资料整理结果见表 20-3。 表 20-3 某地二周患病者门诊医疗卫生服务利用影响因素资料 患者 编号 性别 年龄 年人均收入 医疗保障 距就近医 疗点时间 自感疾病 严重程度 发病 时间 就诊 X1 X2 X 3 X4 X 5 X 6 X7 Y 1 1 4 0 1 2 2 3 1 2 1 4 0 1 1 2 3 0 3 0 4 0 1 1 3 3 0 4 0 3 1 1 2 1 1 0
2 1 0 1645 0 1646 0 4 1647 1 2 1648 4 2 1649 0 5 0 2 2 3 “发病时间”虽为有序多分类变量资料,但目前尚不能确定表203中赋值是否可真实 反映其测度,故以最高值为参照水平,产生2个哑变量。 “发病时间”哑变量: X Xn 1 1 0 0 1 3 0 0 与多重线性回归类似,多因素0g$回归同样存在对自变量的筛选问题,即按事先规 定的检验水平,利用固定的算法,将具有统计意义的变量逐步选入模型,不具有统计意义的 变量剔除在模型外。具体方法有前进法、后退法、逐步法,但检验统计量不再是线性回归中 的F统计量,而是前述的似然比检验统计量G(或x2)、ald统计量等。 本例采用后退法(α=0.05)进行变量筛选。 ()利用似然比检验筛选自变量 表20-4逐步回归过程及模型检验 步骤剔除变量 模型似然比检验x2值自由度 P值 0 无剔除变量 98.9711 8 <0.0001 1 2160.468 98.8693 7 <0.0001 2 X 2160.569 98.7621 6 <0.0001 3 2160.676 96.1755 <0.0001
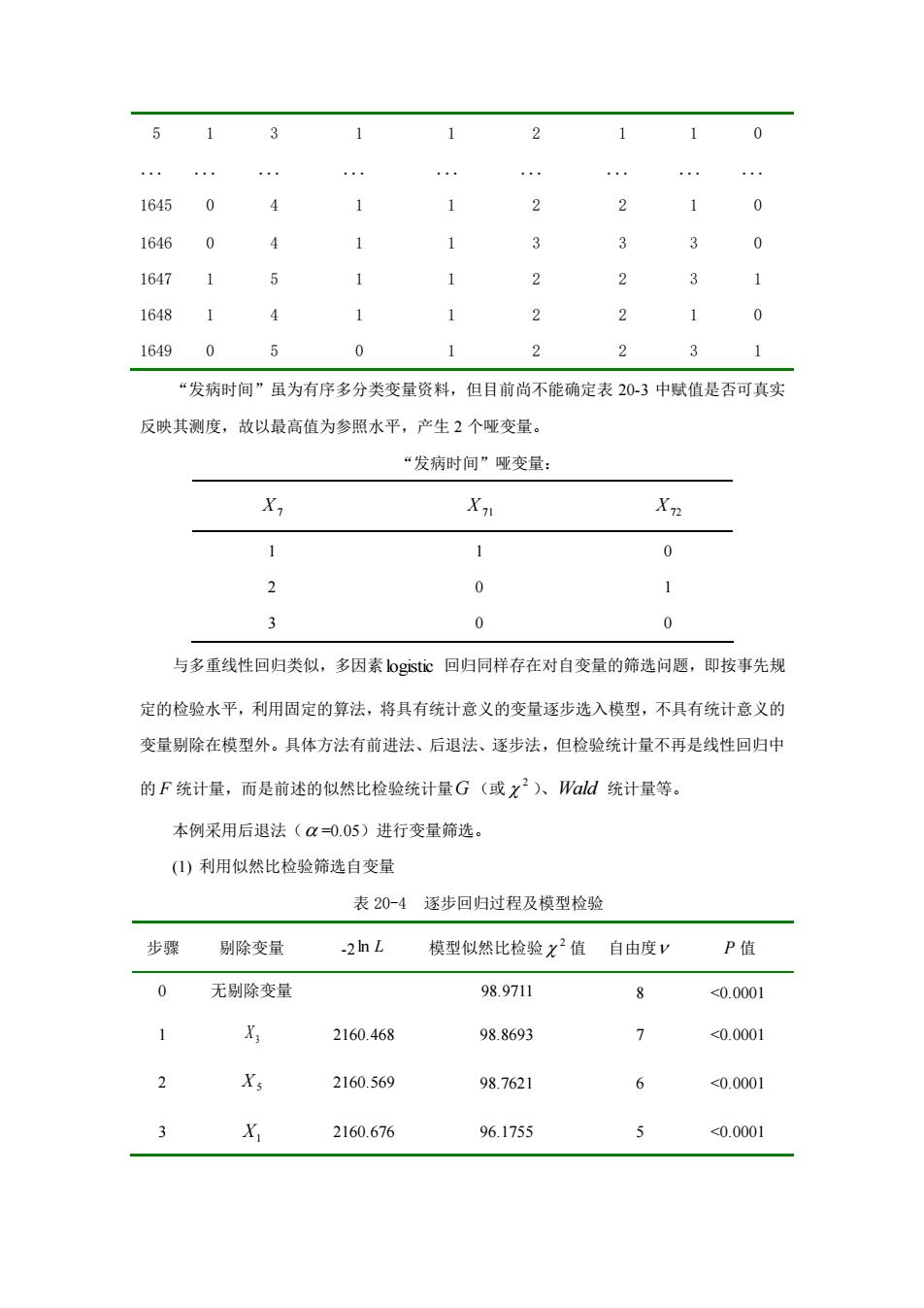
5 1 3 1 1 2 1 1 0 ... ... ... ... ... ... ... ... ... 1645 0 4 1 1 2 2 1 0 1646 0 4 1 1 3 3 3 0 1647 1 5 1 1 2 2 3 1 1648 1 4 1 1 2 2 1 0 1649 0 5 0 1 2 2 3 1 “发病时间”虽为有序多分类变量资料,但目前尚不能确定表 20-3 中赋值是否可真实 反映其测度,故以最高值为参照水平,产生 2 个哑变量。 “发病时间”哑变量: X7 X 71 X72 1 1 0 2 0 1 3 0 0 与多重线性回归类似,多因素 logistic 回归同样存在对自变量的筛选问题,即按事先规 定的检验水平,利用固定的算法,将具有统计意义的变量逐步选入模型,不具有统计意义的 变量剔除在模型外。具体方法有前进法、后退法、逐步法,但检验统计量不再是线性回归中 的 F 统计量,而是前述的似然比检验统计量 G (或 2 )、Wald 统计量等。 本例采用后退法( =0.05)进行变量筛选。 (1) 利用似然比检验筛选自变量 表 20-4 逐步回归过程及模型检验 步骤 剔除变量 -2 ln L 模型似然比检验 2 值 自由度 P 值 0 无剔除变量 98.9711 8 <0.0001 1 X 3 2160.468 98.8693 7 <0.0001 2 X 5 2160.569 98.7621 6 <0.0001 3 X1 2160.676 96.1755 5 <0.0001
4 X 2163.263 93.3326 4 <0,.0001 注:仅有常数项时-2nL=2259.439 模型中仅有常数项时,2hL=2259.439,无剔除变量时-2hL=2160.468。当剔除X,时, 有-2nL=2160.569,似然比检验x2-2160.569-2160.468=0.101,=1,2<xX00 P>0.05,X,可剔除。此时,模型似然比检验X2=2259.439-2160.569-9887,P<0.0001,拒 绝H。,可以认为剔除X,后所建立的ogc回归方程有意义。其余步骤类似,到第4步,在 =0.05水准,再无变量可剔除,故最终保留在方程中的变量有X2、X。、X,。 (②)关于选中变量的参数估计 表20-5关于选中变量的参数估计、Wald检验和OR估计 变量名参数估计值bS。Wald2P值 OR OR95%置信区间 常数项0.4673 0.29762.46470.1164 X2 0.23270.057216.5718<0.00011262 (1.1281.412) -0.6089 0.0768 62.9176 <0.0001 0.544 (0.468,0.632) X -0.5004 0.119317.5977<0.0001 0.606 (0.480,0.766) -0.34030.18493.3893 0.0656 0.712 (0.495,1.022) 注X,:Wald x2=17.9084,df=2,P=0.0001 由X,生成了2个哑变量X71X2,对X2有ldx2=3.3893,P>0.05,但这2 个哑变量应作为一个整体进行筛选。 进入模型的变量有X2、X6、X、X2,相应的OR估计值分别为1262、0.544、0.606 和0.712,0R的95%置信区间分别为(1.128,1.412)、(0.468,0.632)、(0.480,0766) 和(0.495,1.022),故可以认为年龄X2、自感疾病严重程度X6和发病时间X,是两周患 病者就诊的影响因素。 最终得到的logistic回归方程为:
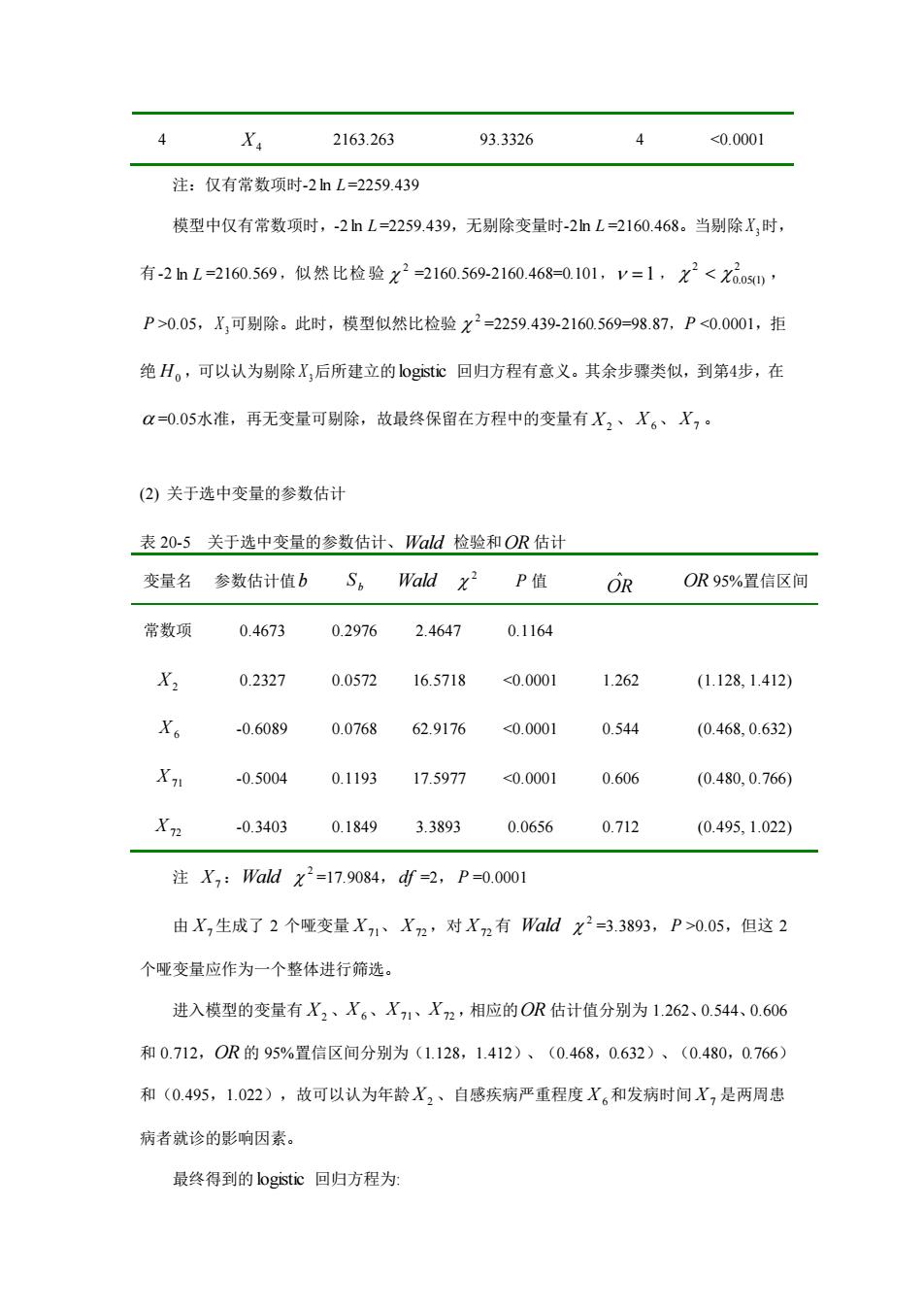
4 X4 2163.263 93.3326 4 <0.0001 注:仅有常数项时-2 ln L =2259.439 模型中仅有常数项时,-2 ln L =2259.439,无剔除变量时-2 ln L =2160.468。当剔除 X 3 时, 有-2 ln L =2160.569 ,似然比检验 2 =2160.569-2160.468=0.101, =1 , 2 0.05(1) 2 , P >0.05,X 3 可剔除。此时,模型似然比检验 2 =2259.439-2160.569=98.87,P <0.0001,拒 绝 H0 ,可以认为剔除 X 3 后所建立的 logistic 回归方程有意义。其余步骤类似,到第4步,在 =0.05水准,再无变量可剔除,故最终保留在方程中的变量有 X2 、 X 6 、 X7 。 (2) 关于选中变量的参数估计 表 20-5 关于选中变量的参数估计、Wald 检验和 OR 估计 变量名 参数估计值 b b S Wald 2 P 值 OR OR 95%置信区间 常数项 0.4673 0.2976 2.4647 0.1164 X2 0.2327 0.0572 16.5718 <0.0001 1.262 (1.128, 1.412) X 6 -0.6089 0.0768 62.9176 <0.0001 0.544 (0.468, 0.632) X 71 -0.5004 0.1193 17.5977 <0.0001 0.606 (0.480, 0.766) X72 -0.3403 0.1849 3.3893 0.0656 0.712 (0.495, 1.022) 注 X7 :Wald 2 =17.9084, df =2, P =0.0001 由 X7 生成了 2 个哑变量 X 71、 X72 ,对 X72 有 Wald 2 =3.3893, P >0.05,但这 2 个哑变量应作为一个整体进行筛选。 进入模型的变量有 X2 、X 6、X 71、X72 ,相应的 OR 估计值分别为 1.262、0.544、0.606 和 0.712,OR 的 95%置信区间分别为(1.128,1.412)、(0.468,0.632)、(0.480,0.766) 和(0.495,1.022),故可以认为年龄 X2 、自感疾病严重程度 X 6 和发病时间 X7 是两周患 病者就诊的影响因素。 最终得到的 logistic 回归方程为: