2.27某系统由两个电机构成,并通过柔性传送带将电机藕合在一起,传送带还将经过 一个摆臂,摆臂上装有用来测量带速与张力的传感器.该系统的基本控制问题是,通过改变 电机转矩来调节传送带的速度与张力.此系统的框图模型如图P2.27所示,试计算 Y(s)/R(s),并确定使Y,与R独立的条件. 2.28某系统的信号流图如图P2.28示,试计算传递函数G(s)=Y(s)/R(s),若进一步 希望实现Y,(s)与R(s)解耦,即希望G(s)=0,请根据其它的G(s)选择合适的G(s). -H2 G G G: RI 速度输入 Gs 速度 Gs G6 G G R2 o Y: R2 O- 张力输入 张力 Hi -H2 图P227速度-张力控制系统 图P2.28系统信号流图 2.29利用梅逊公式求出图P2.29中所示系统的总增益. R(s) C(s) a 0 (a) R(s) C(s) 0 (b) N(s)9 E(s) C(s) G G G: (c) G2 g R(s) G8 0 C(s) G2 -H2 (d) 图P2.29系统的信号流图 10
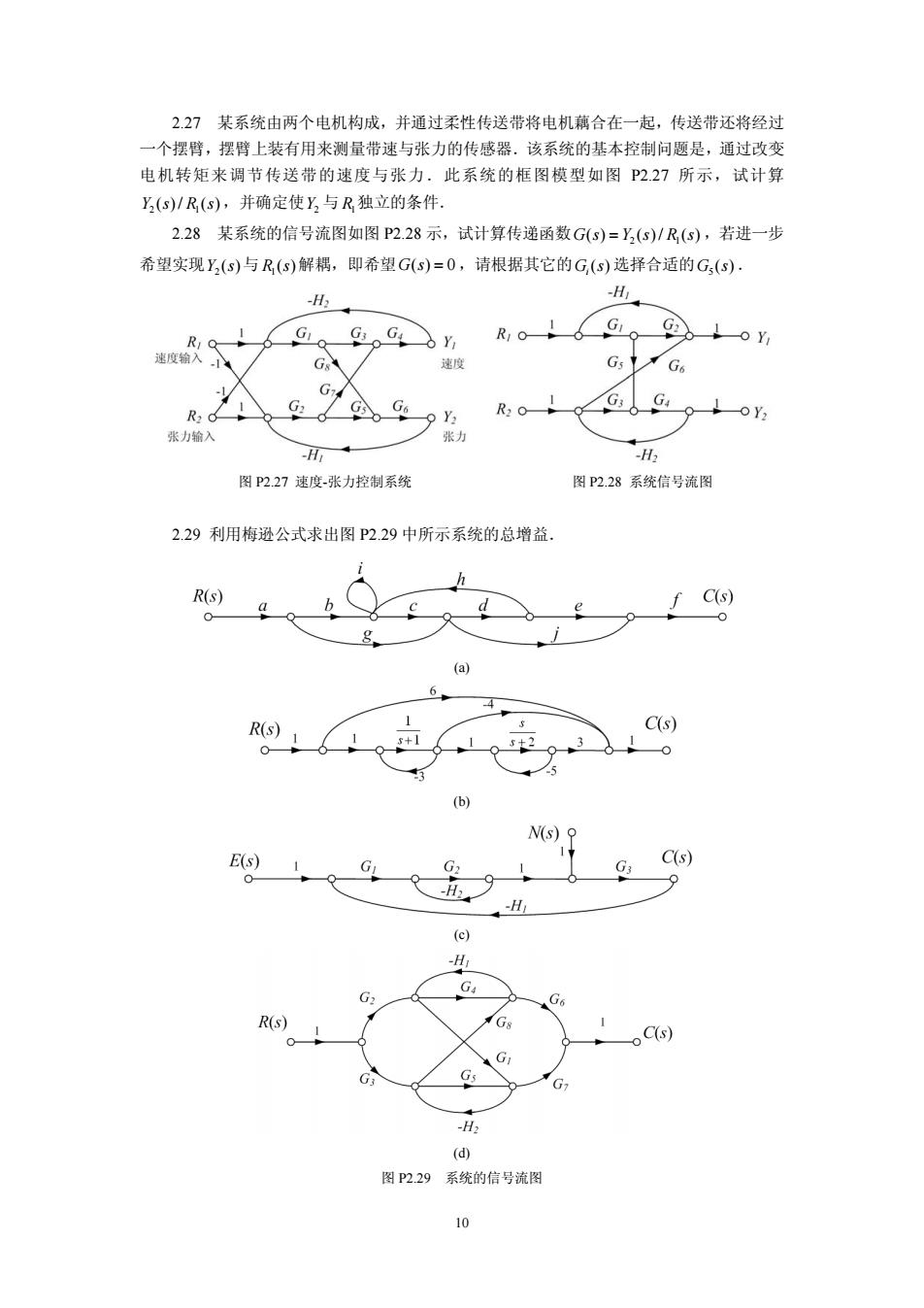
10 2.27 某系统由两个电机构成,并通过柔性传送带将电机藕合在一起,传送带还将经过 一个摆臂,摆臂上装有用来测量带速与张力的传感器.该系统的基本控制问题是,通过改变 电机转矩来调节传送带的速度与张力.此系统的框图模型如图 P2.27 所示,试计算 2 1 Ys Rs ( )/ ( ),并确定使Y2 与 R1独立的条件. 2.28 某系统的信号流图如图 P2.28 示,试计算传递函数 2 1 Gs Y s R s ( ) ( )/ ( ) = ,若进一步 希望实现 2 Y s( )与 1 R ( )s 解耦,即希望G s() 0 = ,请根据其它的 ( ) G s i 选择合适的 5 G s( ) . 图 P2.27 速度-张力控制系统 图 P2.28 系统信号流图 2.29 利用梅逊公式求出图 P2.29 中所示系统的总增益. (a) (b) (c) (d) 图 P2.29 系统的信号流图

第三章 频率特性 3.1己知系统的传递函数为 10 G(s=- 1+0.5s 求在频率为∫=1HZ,幅值rm=10的正弦输入信号作用下,系统的稳态输出c()的幅值与相 位. 3.2设单位反馈控制系统的开环传递函数为 G6)=10 5+1’ 当系统输入信号 (1)r(t)=sin(t+30): (2)r(t)=2c0s(2t-45): 作用下,试求系统的稳态输出. 3.3绘制下述环节的幅相频率特性Gjo),幅频特性A(o),相频特性p(o). 3 (1)G(s)=1.5e 2)G(s)=0.2s+1 (3)Gs)=02s-1 3 3.4己知系统方块图如P3.4所示 (1)试写出系统的频率特性谱,即幅相频率特性G(jo),幅频特性A(o),相频特性(o), 实频特性U(o,虚频特性V(o)的表达式: (2)绘出K=100,T=ls,T2=5s时系统的Nyuist图,并求出系统的无阻尼自然频率0n· K C(s) R(s) 5 C(s) R(s) s(8+2) Ts+I(Ts+1) 图P3.4系统方块图 图P3.5系统方块图 3.5已知系统方块图如P3.5所示.试确定系统的谐振峰值,谐振频率及截止频率. 3.6画出下列给定传递函数的幅相频率特性,试问这些曲线是否穿越实轴,若是,则求 出与实轴的交点的频率及相应的幅值, 1 (1)G(s)= (2)G(s)= 1 (3) (s+1)(s+2) s(s+1)(s+2) G)=g(s+1s+2) 3.7绘出下列三个传递函数的波德图(其中T>T,>0),并进行比较. (0Gs)= Tis+1 Ts+1 (2②)G)=二7s+1 (3)G(s)= Tis-1 T,s+1 Ts+1 3.8若系统的单位阶跃响应为 11
11 第三章 频率特性 3.1 已知系统的传递函数为 s G s 1 0.5 10 ( ) + = . 求在频率为 f = 1HZ,幅值rm = 10的正弦输入信号作用下,系统的稳态输出c(t)的幅值与相 位. 3.2 设单位反馈控制系统的开环传递函数为 1 10 ( ) + = s G s , 当系统输入信号 (1)r(t) = sin(t + 30°) ; (2)r(t) = 2cos(2t − 45°) ; 作用下,试求系统的稳态输出. 3.3 绘制下述环节的幅相频率特性G( jω) ,幅频特性 A(ω),相频特性ϕ(ω) . (1) s G s e− ( ) = 1.5 (2) 0.2 1 3 ( ) + = s G s (3) 0.2 1 3 ( ) − = s G s 3.4 已知系统方块图如 P3.4 所示 (1)试写出系统的频率特性谱,即幅相频率特性G( jω) ,幅频特性 A(ω),相频特性ϕ(ω) , 实频特性U(ω) ,虚频特性V (ω)的表达式; (2)绘出 K = 100 ,T 1s 1 = ,T 5s 2 = 时系统的 Nyuist 图,并求出系统的无阻尼自然频率ωn . 图 P3.4 系统方块图 图 P3.5 系统方块图 3.5 已知系统方块图如 P3.5 所示.试确定系统的谐振峰值,谐振频率及截止频率. 3.6 画出下列给定传递函数的幅相频率特性,试问这些曲线是否穿越实轴,若是,则求 出与实轴的交点的频率及相应的幅值. (1) ( 1)( 2) 1 ( ) + + = s s G s (2) ( 1)( 2) 1 ( ) + + = s s s G s (3) ( 1)( 2) 1 ( ) 2 + + = s s s G s 3.7 绘出下列三个传递函数的波德图(其中 0 T1 > T2 > ),并进行比较. (1) 1 1 ( ) 2 1 + + = T s T s G s (2) 1 1 ( ) 2 1 + − + = T s T s G s (3) 1 1 ( ) 2 1 + − = T s T s G s 3.8 若系统的单位阶跃响应为