上泽成大坐 上浙克1大当 总体要求 现代控制工程复习 >掌握概念 >能建立分析与设计的思路 >能应用基本或重要公式与定理 >能将解析式与方块图互为映照 >知识重点是现代控制理论部分(90%) 上承文点大皆 上活文1大举 对控制系统的基本认识 控制系统的构成 ·具有性能要求的系统 主要的构成元素有哪些? ·具有反馈纠差的特点 构建出来的框图是怎样的? ·稳定性的确保 控制系统大致怎样运行的? ·适当控制策略的应用 ·适当的性价比 讨论: 炉温控制的大致实现? 上泽元1大孝 第一章、动态系统的数学模型 上活丝大举 炉温闭环控制系统 与状态空间的系统描述 -) ·控制系统数学模型的意义 ☒ ·控制系统数学模型的分类 ·机电系统数学模型的建立 -220v 护温闭环控制系统图 1-热电偶2-加热器 1
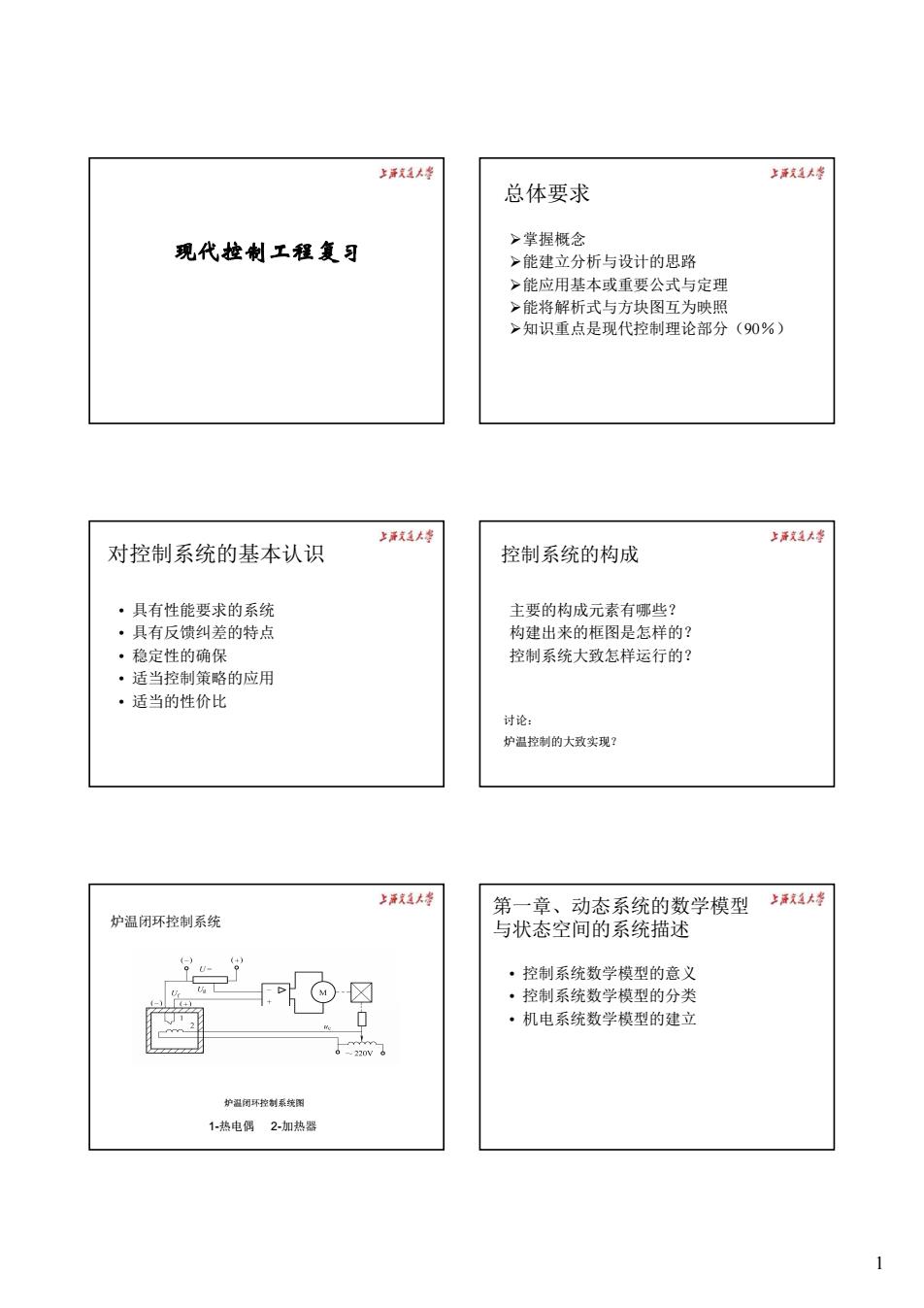
1 现代控制工程复习 总体要求 ¾掌握概念 ¾能建立分析与设计的思路 ¾能应用基本或重要公式与定理 ¾能将解析式与方块图互为映照 ¾知识重点是现代控制理论部分(90%) 对控制系统的基本认识 • 具有性能要求的系统 • 具有反馈纠差的特点 • 稳定性的确保 • 适当控制策略的应用 • 适当的性价比 控制系统的构成 主要的构成元素有哪些? 构建出来的框图是怎样的? 控制系统大致怎样运行的? 讨论: 炉温控制的大致实现? 炉温闭环控制系统图 1-热电偶 2-加热器 炉温闭环控制系统 第一章、动态系统的数学模型 与状态空间的系统描述 • 控制系统数学模型的意义 • 控制系统数学模型的分类 • 机电系统数学模型的建立

上泽成大坐 上浙克1大当 知识点 机械系统的组成 ·状态空间表达式相关概念的定义 ·状态空间表达式的获得 一般由三种单元组成: ·几种典型的状态空间表达式 质量(惯性力):Fm=ma ·状态空间表达式的转换(状态变量的线 弹簧:F=cr 性变换) 阻尼:F=cw ·状态空间表达式与传递函数的关系 由这三种消耗力与施加力构成平衡方程式 上承文点大皆 上活文1大举 概念提示 圆 状态空间表达式对多输入多输出系统的描述 ·状态、状态变量、状态向量、状态空间 二输入二输出二阶系统的动态方程: 表达式、状态方程、输出方程、动态方 主1=a11x1+e12x2+b11u1+b12u2 程 ·能控标准型、对角线标准型、普通型 i2=a2ix1+a22x2+b21u1+b2m42 ·状态向量线性变换、线性变换阵 y1=C1x1+C12x2 y2=c21x1+C22T2 试画出相应的方块图 上部成1大孝 例 求状态空间模型 上活丝大举 方块图(直观体现各个单元之间的关系) [--6] 1 [-6Lr88] 的传递函数 器器 品品 2
2 知识点 • 状态空间表达式相关概念的定义 • 状态空间表达式的获得 • 几种典型的状态空间表达式 • 状态空间表达式的转换(状态变量的线 性变换) • 状态空间表达式与传递函数的关系 机械系统的组成 一般由三种单元组成: 质量(惯性力):Fm=ma 弹簧:Fk=kx 阻尼:Fc=cv 由这三种消耗力与施加力构成平衡方程式 概念提示 • 状态、状态变量、状态向量、状态空间 表达式、状态方程、输出方程、动态方 程 • 能控标准型、对角线标准型、普通型 • 状态向量线性变换、线性变换阵 状态空间表达式对多输入多输出系统的描述 二输入二输出二阶系统的动态方程: 试画出相应的方块图 例 方块图(直观体现各个单元之间的关系) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − =⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 2 1 2 1 2 1 0 1 1 1 25 4 0 1 u u x x x x & & ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 2 1 2 1 2 1 0 0 0 0 0 1 1 0 u u x x y y ( ) ( ) 1 1 U s Y s ( ) ( ) 1 2 U s Y s ( ) ( ) 2 1 U s Y s ( ) ( ) 2 2 U s Y s 求状态空间模型 的传递函数 例

上泽成大坐 上浙克1大当 = 3+4 A=01g-25-4 U(s)s2+4s+25 B=11:01: C=10:01]: -25 D=00:001 0,(932+4s+25 [numl,den1]=ss2tf(A.B.C.D.1) [num2,den2]=ss2tf(A,B,C,D,2) Y(s) s+5 1: 26+45+25 2 Y2(s) 3-25 U2(s)s2+4s+25 )承文点人岁 上活文1大修 例 传递函数化成 3 W(s)产(6+1s+2(5+4 设系统的微分方程为 ++, y+7y+145+8y=3w 根据 求对角线标准型的状态空间描述 u-多,0o) c=ms-A)ws) 上泽元1大孝 上活丝大修 1=s+1Dw()=m5+2+4=1 s+2)w()=吗石+说+0-是 =四(&+4)w()=g++2-支 于是 4 -1 0 07 fr 文= 0 -2 0x+ 0 0 -4 y=1 3 1 2 2 3
3 A=[0 1;-25 -4]; B=[1 1;0 1]; C=[1 0;0 1]; D=[0 0;0 0]; [num1,den1]=ss2tf(A,B,C,D,1) [num2,den2]=ss2tf(A,B,C,D,2) 1:u1 2:u2 4 25 4 ( ) ( ) 2 1 1 + + + = s s s U s Y s 4 25 25 ( ) ( ) 2 1 2 + + − = U s s s Y s 4 25 5 ( ) ( ) 2 2 1 + + + = s s s U s Y s 4 25 25 ( ) ( ) 2 2 2 + + − = s s s U s Y s , . 求对角线标准型的状态空间描述 例 根据
开我道大岁 上浙克1大当 第二章:系统的时域分析与状态 知识点 方程的解 >什么是时域分析? ·矩阵指数的定义、计算 >控制系统性能的时域评价? ·齐次与非齐次状态方程的解及其含义 >Simulink时域仿真的对照认识(能作仿 真) 0=e一H可eaM:h 例 i=Ax+bu 上所文且大坐 -2-3 输入为单位阶跃函数 解一: 2e'-e2 e-e2 曾计算得: e= -2e+2e-2r-e'+2e-i tw- 上潘成1大孝 上活丝大举 第三章:系统的稳定性分析 知识点 >李氏稳定性的定义 >概念:平衡状态(点)、渐进稳定、大范 围渐进稳定等 >李氏稳定性的判别(间接法、直接法) >李氏函数的设定 ~线性定常系统的应用P+PA--Q 4
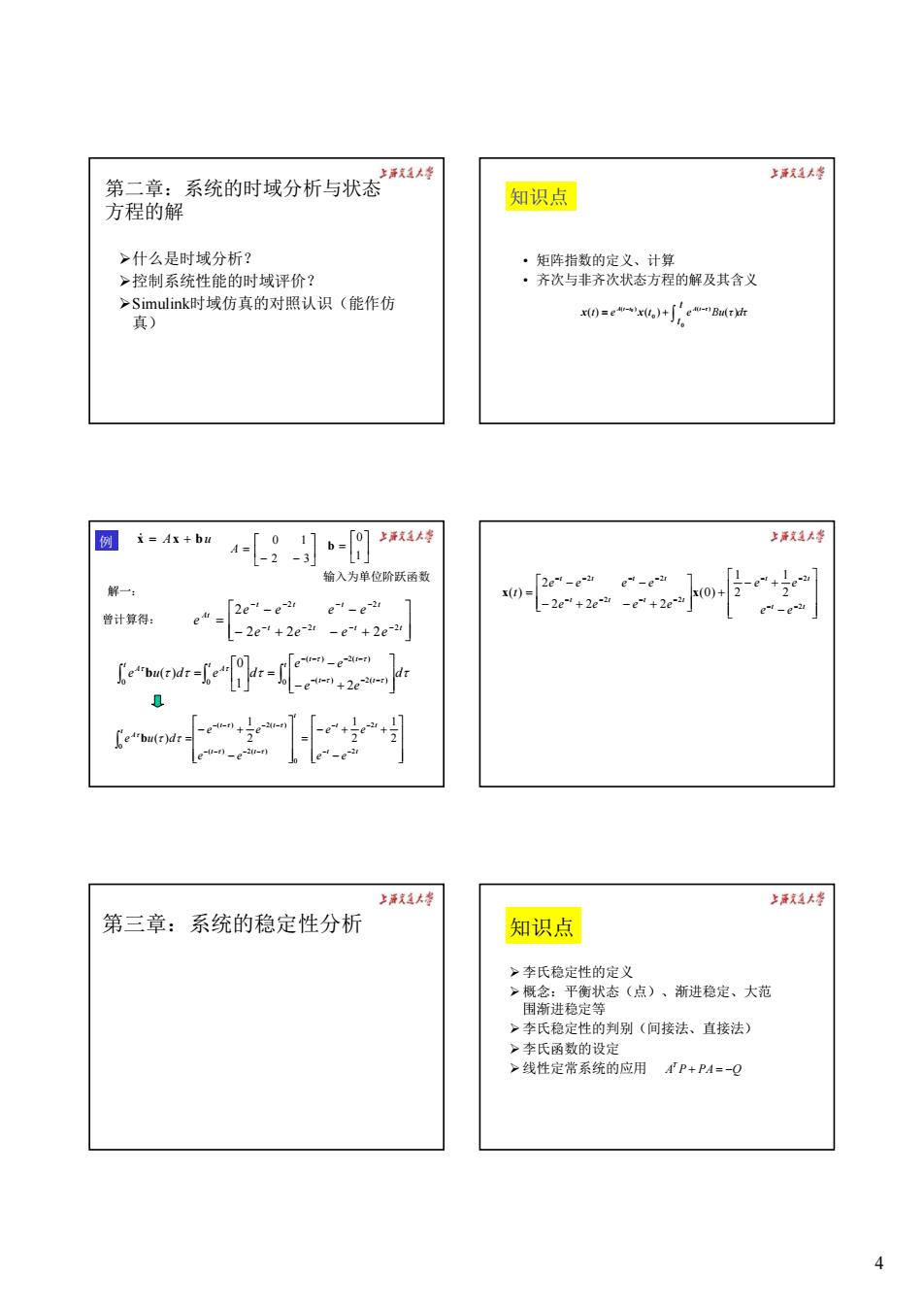
4 第二章:系统的时域分析与状态 方程的解 ¾什么是时域分析? ¾控制系统性能的时域评价? ¾Simulink时域仿真的对照认识(能作仿 真) • 矩阵指数的定义、计算 • 齐次与非齐次状态方程的解及其含义 知识点 e Bu τ dτ t t t e t A t t A t τ ∫ − − ( ) = ( ) + ( ) ( ) 0 0 ( ) 0 x x ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − = 2 3 0 1 A x& = Ax + bu ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 1 0 b ∫ ∫ ∫ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − − − − − − − − t t t t t t A t A d e e e e e u d e d 0 0 ( ) 2( ) ( ) 2( ) 0 1 2 0 (τ ) τ τ τ τ τ τ τ τ τ b ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + − + − − = − − − − − − − − t t t t t t t t At e e e e e e e e e 2 2 2 2 2 2 2 2 曾计算得: ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − + + = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − + = − − − − − − − − − − − − ∫ t t t t t t t t t t A e e e e e e e e e u d 2 2 0 ( ) 2( ) ( ) 2( ) 0 2 1 2 1 2 1 ( ) τ τ τ τ τ b τ τ 输入为单位阶跃函数 解一: 例 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − + + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + − + − − = − − − − − − − − − − − − t t t t t t t t t t t t e e e e e e e e e e e e t 2 2 2 2 2 2 2 1 2 1 (0) 2 2 2 2 x( ) x 第三章:系统的稳定性分析 知识点 ¾李氏稳定性的定义 ¾概念:平衡状态(点)、渐进稳定、大范 围渐进稳定等 ¾李氏稳定性的判别(间接法、直接法) ¾李氏函数的设定 ¾线性定常系统的应用 T A P PA Q + =−

上泽成大坐 上播克1大当 例 考察下列系统在平衡状态处的稳定性。 =x2 :=-9(1+x)2x2-x1B>0 V(x)=x+x克>0 (x)=2x1i1+2x22=-20(1+x2x3 考察(x): 当x2=0,x1≠0时,有(x)=0 当工2=-1,z1≠0时,有Vx)=0 其余情况下,(x)<0。 上承文点大皆 上活文1大举 第四章:线性系统的能控性和能观性 反设(x)=0这时存在两种情汽:z2(:)=0及x1任意:x(:)=-1及x1任意。 先看第一种情况2()=0登球若x(:)=0和2(t)=0,将其代人原状态方程得 r(:)=0和()=D。所以在这种情况下,只有平衡状泰=z2=0才满足(x)=0 再看第二种情视。2(t》=-1意味着x2(:》司-1和2(:》要0:格其代人原秋都方程得 出x《:)二0和}=一1。这个结果是矛盾的。所以这种情况不会发生在方程的解运动轨线 上e 因此,系统在原点处的平衡状态是渐近意定的。 上泽元1大孝 上活丝大举 知识点 例 ·能控能观的定义 能控标准型的系统必能控。以三阶系统为例说明 ·能控能观的意义 ·能控能观的判别:判别阵、对角线标准 型 5
5 例 第四章:线性系统的能控性和能观性 • 能控能观的定义 • 能控能观的意义 • 能控能观的判别:判别阵、对角线标准 型 知识点 能控标准型的系统必能控。以三阶系统为例说明 例