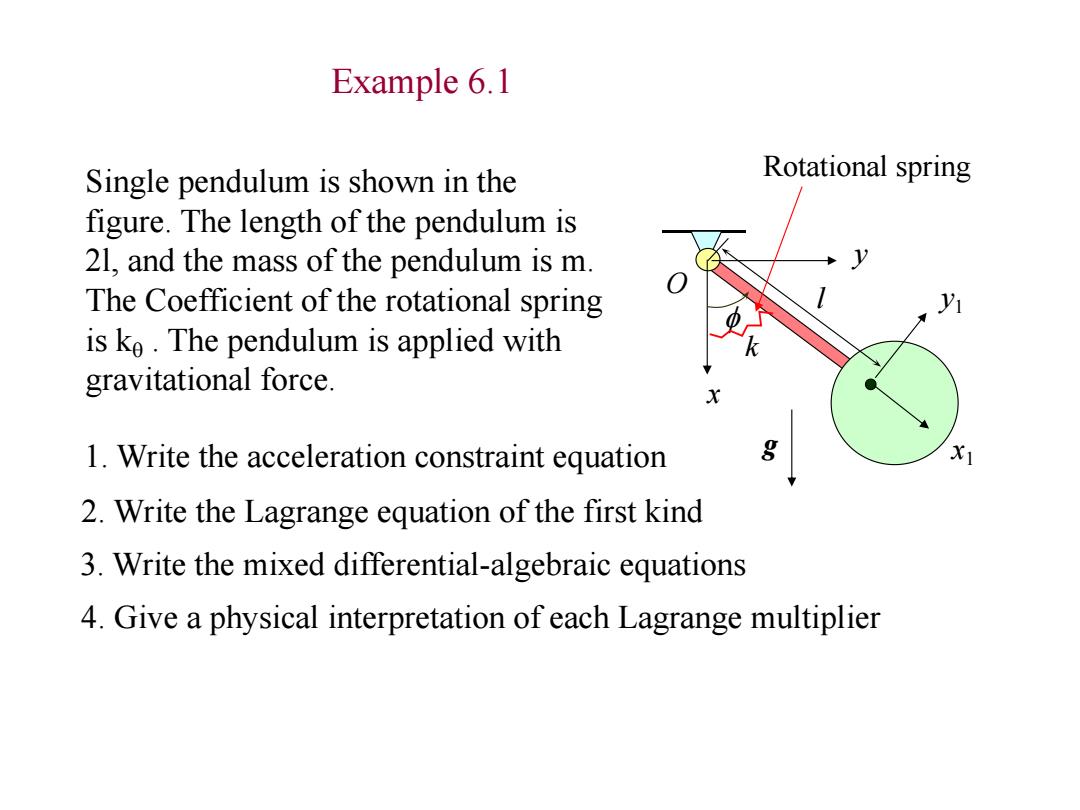
Example 6.1 Single pendulum is shown in the Rotational spring figure.The length of the pendulum is 21,and the mass of the pendulum is m. The Coefficient of the rotational spring is ke.The pendulum is applied with gravitational force. 1.Write the acceleration constraint equation X1 2.Write the Lagrange equation of the first kind 3.Write the mixed differential-algebraic equations 4.Give a physical interpretation of each Lagrange multiplier
Example 6.1 g x y x1 y1 O f l k Rotational spring Single pendulum is shown in the figure. The length of the pendulum is 2l, and the mass of the pendulum is m. The Coefficient of the rotational spring is kq . The pendulum is applied with gravitational force. 2. Write the Lagrange equation of the first kind 1. Write the acceleration constraint equation 4. Give a physical interpretation of each Lagrange multiplier 3. Write the mixed differential-algebraic equations
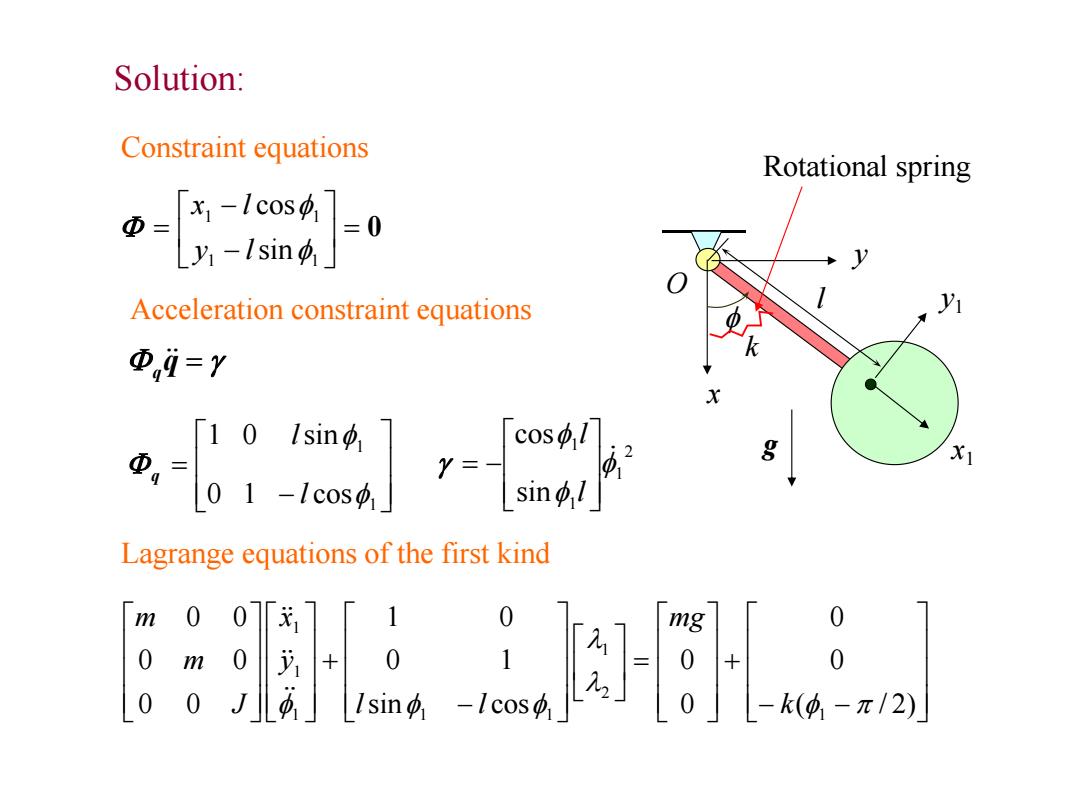
Solution: Constraint equations Rotational spring [· Acceleration constraint equations Φ,i=Y Lagrange equations of the first kind m001 0 0 m 0 0
Solution: g x y x1 y1 O f l 0 1 1 1 1 sin cos f f y l x l 1 1 0 1 cos 1 0 sin f f l l q 2 1 1 1 sin cos f f f l l Constraint equations Lagrange equations of the first kind ( / 2) 0 0 0 0 sin cos 0 1 1 0 0 0 0 0 0 0 1 2 1 1 1 1 1 1 f l l f f f k mg l l y x J m m k Rotational spring Acceleration constraint equations q q

Mixed algebraic and differential equations m 0 0 0 mg 0 m 0 0 1 或 0 0 0 J Isin -Icos -k(-π/2) 0 Isin 0 0 -中2c0s4 0 1 -Icos 0 0 2 -sin 戈=-l0,2cos,-lsin,,戈=-l0,2sin+lcos,功 =mg-m mg +m(1ocoso+Isin),=-mi m(1o sin-lcos) 0 J=-k(,-π/2)-lsin,21+1cos,22=-k(4,-π/2)-Img sin4-ml24, 0 (J+ml2)=-k(d -/2)-Img sin 0 元1,1,九1,几2
Mixed algebraic and differential equations 1 2 1 1 2 1 1 2 1 1 1 1 1 1 1 1 sin cos ( / 2) 0 0 1 cos 0 0 1 0 sin 0 0 0 0 sin cos 0 0 0 1 0 0 1 0 f f f f f l l f f f f f k mg y x l l J l l m m 1 1 1 2 1 1 1 1 1 2 1 1 f cosf sinf f , f sinf cosf f x l l y l l ( cos sin ), ( sin cos ) 1 1 1 2 1 1 1 2 1 1 2 l1 1 f1 f f f l f f f f mg mx mg m l l my m l l 1 2 1 1 1 1 1 2 1 1 f (f / 2) sinf l cosf l (f / 2) sinf f m J k l l k lmg l 1 1 1 2 (J ml )f k(f / 2) lmg sinf 1 1 1 2 x , y , l , l
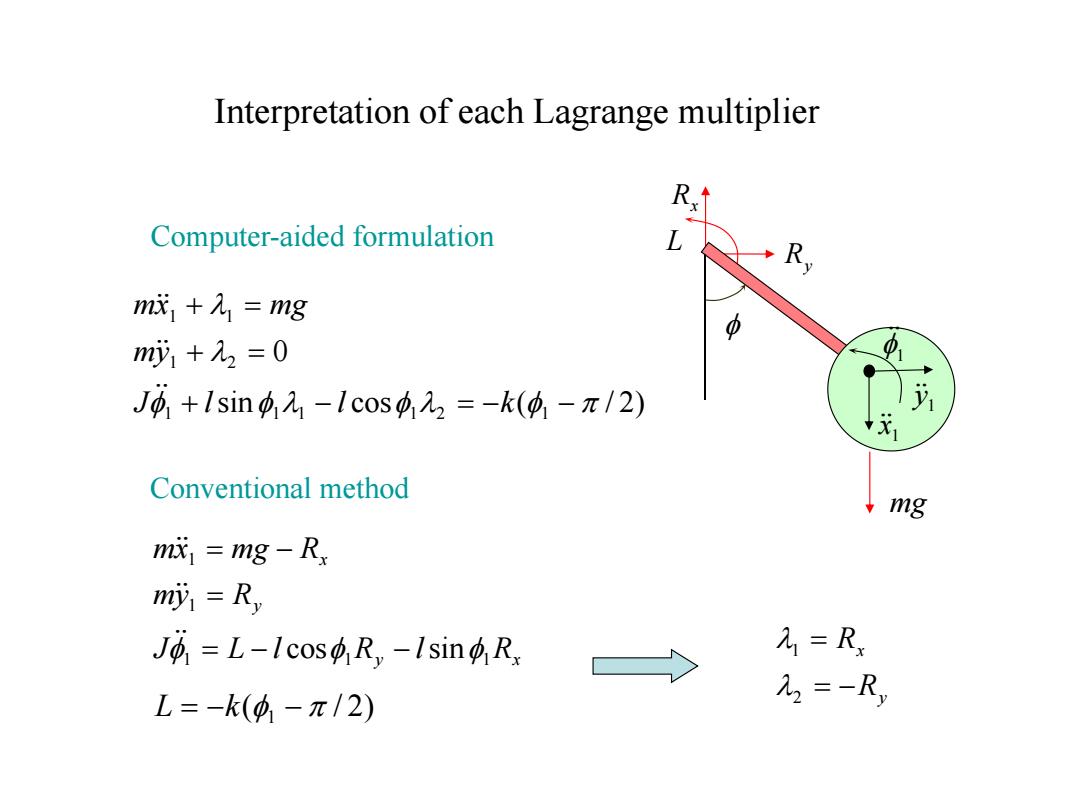
Interpretation of each Lagrange multiplier Computer-aided formulation L m成1+人1=mg 中 my1+22=0 1 J中,+1sin-1cos422=-k(,-π/2) Conventional method mg m=mg-R my=Ry Jo=L-Icos R,-Isin R =R 〉 L=-k(-π/2) 元2=-R
Interpretation of each Lagrange multiplier sin cos ( / 2) 0 1 1 1 1 2 1 1 2 1 1 f f l f l f l l J l l k my mx mg Conventional method mg Rx Ry L y x y x J L l R l R my R mx mg R 1 1 1 1 1 f cosf sinf ( / 2) L k f1 1 x 1 y f1 f Computer-aided formulation y x R R 2 1 l l

Example 6.2 A sliding link Consider a link,the left end can slide along the wall,and the right end can slide on the ground.Friction is not taken into account.The mass of the link is m, and the length of the link is / (1)Write the constraint equations (2)Write the Lagrange dynamic equations of the first kind (3)Give physics interpretation for each Lagrange Multiplier (4)Write the mixed differential- algebraic equations (5)Derive the Lagrange dynamic equations of the second kind
Example 6.2 A sliding link Consider a link, the left end can slide along the wall, and the right end can slide on the ground. Friction is not taken into account. The mass of the link is m, and the length of the link is l. x 1 y 1 x yf f1 (1) Write the constraint equations (2) Write the Lagrange dynamic equations of the first kind (3) Give physics interpretation for each Lagrange Multiplier (4) Write the mixed differential- algebraic equations (5) Derive the Lagrange dynamic equations of the second kind