
6.5 Equilibrium Problem Equilibrium Definition A system is said to be in equilibrium if it remains stationary under the action of applied forces i=9=0 Dynamic equation M9+Φ,'=2 i=0 Equilibrium equation D,九=
q q 0 T A Mq q Q T A q Q A system is said to be in equilibrium if it remains stationary under the action of applied forces Equilibrium Definition Dynamic equation Equilibrium equation q 0 6.5 Equilibrium Problem

Equilibrium Condition Solve Φ,2=04 and 1Φ(q)=0 Since they are nonlinear algebraic equations,Newton-Raphson Method can be used for solution,however,the initial value of A is difficult to estimate q=u'v v:Independent coordinates To solve this problem,transformation method is used 0,=②。中]0 Φ1=2 e Φ,九=2, →=(西,0 Equilibrium Condition H'Q=2,H=ΦΦ
Equilibrium Condition Solve T A q Q and (q) 0 Since they are nonlinear algebraic equations, Newton-Raphson Method can be used for solution, however, the initial value of is difficult to estimate To solve this problem, transformation method is used q u v A v T A u T Q Q v u A u T u Q 1 A v A u A Q Q Q A v A u T H Q Q H u v 1 Equilibrium Condition v: Independent coordinates T T T q u v

Example 6.10 X Single pendulum is shown in the figure.The length of the pendulum is 21,and the mass of the pendulum is m.The Coefficient of the rotational spring is ke.The pendulum is applied with gravitational force.Find the equilibrium condition g X1
Example 6.10 x1 y1 C x y f g kq Single pendulum is shown in the figure. The length of the pendulum is 2l, and the mass of the pendulum is m. The Coefficient of the rotational spring is kq . The pendulum is applied with gravitational force. Find the equilibrium condition
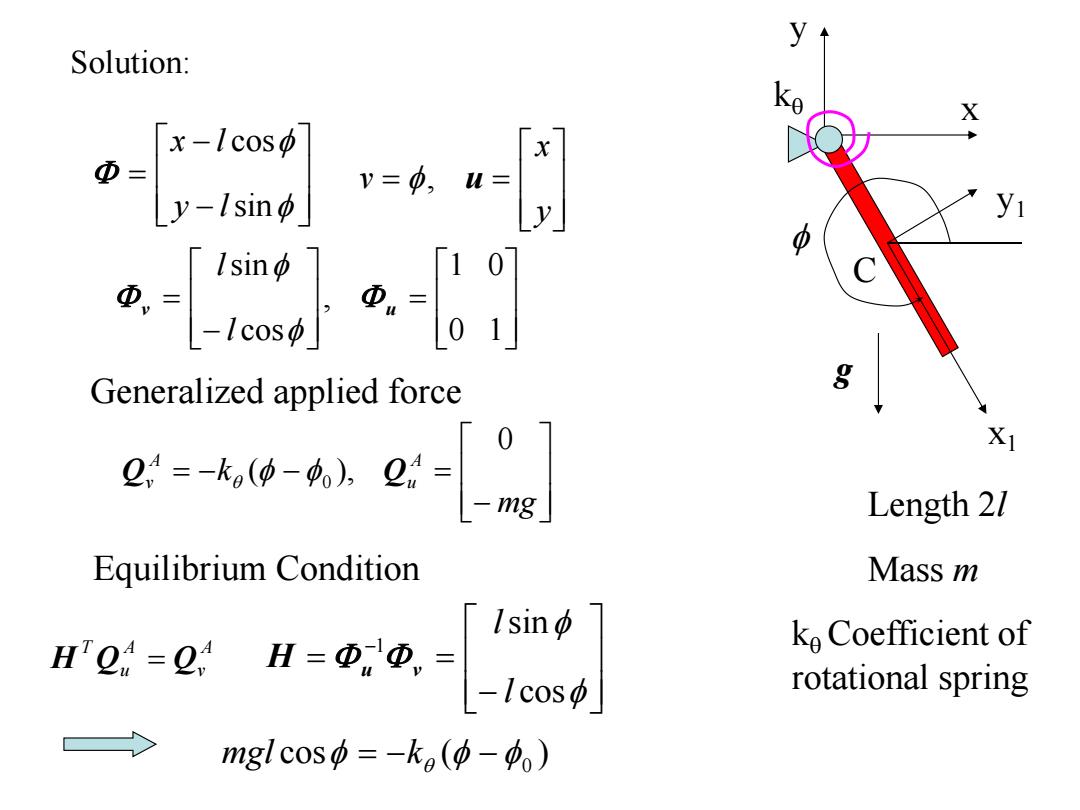
Solution: X x-lcosφ Φ= -1sn v=0,u= y 10 Generalized applied force g e-wse-l Length 21 Equilibrium Condition Mass m [lsinφ I2:-Q:H-losd ko Coefficient of rotational spring mgl cos中=-kg(p-中)
x1 y1 C x y f g Length 2l Mass m kq kqCoefficient of rotational spring 0 1 1 0 , cos sin v u f f l l f f sin cos y l x l y x v f, u Equilibrium Condition A v A u T H Q Q Generalized applied force mg k A u A v 0 ( ), Q q f f 0 Q f f cos sin 1 l l H u v cos ( ) f q f f 0 mgl k Solution:

Example 6.11 Double pendulum is shown in the figure.The length of each link is 27,and X the mass of each link is m.A horizontal Br force is applied at the tip point of B2 y1 Each pendulum is applied with gravitational force.Find the 中1 equilibrium condition g X 2 p2 F X2
Example 6.11 x1 y1 C1 x y f1 g x2 y2 C2 f2 F P Double pendulum is shown in the figure. The length of each link is 2l, and the mass of each link is m. A horizontal force is applied at the tip point of B2 . Each pendulum is applied with gravitational force. Find the equilibrium condition B2 B1