
导体色散 ■ 金属原子的电子谐振频率远落于紫外光谱以外, 导体的介电常数可以认为是ε,即导体的等效复 介电常数E为: Ne m(q+j0】 AN.EDU.CN lexu@mail.xidian.edu.cn 12
lexu@mail.xidian.edu.cn 12 导体色散 金属原子的电子谐振频率远落于紫外光谱以外, 导体的介电常数可以认为是ε0,即导体的等效复 介电常数εc为: 2 0 0 ( ) c Ne j j mq j ε ε σε ω =− =− + XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

相速与群速 B ■对于理想介质B=√u8 。相速度与频率无关 ·非色散介质 。若B与ω不满足正比关系,则相速度与频率相关,成为色 散介质。 ·当频率足够高时,E是ω的函数,因而B是ω的复杂函数, 介质成为色散介质: 。对于导电介质,相速度与频率相关,是色散介质。 。良导体中的相速: 20 Up= B uo lexu@mail.xidian.edu.cn 13
lexu@mail.xidian.edu.cn 13 相速与群速 对于理想介质 • 相速度与频率无关 • 非色散介质 若β与ω不满足正比关系,则相速度与频率相关,成为色 散介质。 • 当频率足够高时,ε是ω的函数,因而β是ω的复杂函数, 介质成为色散介质; • 对于导电介质,相速度与频率相关,是色散介质。 • 良导体中的相速: p v ω β = β ω µε = µσ ω β ω υ 2 p == XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

相速与群速 空间、时间上无限延伸的单一频率电磁波称为单色波 ·单一频率的正旋电磁波不传递任何信息 。理想的单频正旋电磁波不存在 ■有限时间、空间传播的电磁波是由不同频率的正旋波(谐 波)叠加而成,称为非单色波 ·非单色波传播过程中,各谐波分量相速不同造成其相 对相位发生变化,引起信号波形变形; 。携带信息的电磁波是具有一定带宽的已调制非单色波, 包络的传播速度才是信号的传递速度 ● 非单色波在色散介质中各个单频分量以不同的相速传 播,非单色波携带信号的传递速度是多少? lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 14 相速与群速 空间、时间上无限延伸的单一频率电磁波称为单色波 • 单一频率的正旋电磁波不传递任何信息 • 理想的单频正旋电磁波不存在 有限时间、空间传播的电磁波是由不同频率的正旋波(谐 波)叠加而成,称为非单色波 • 非单色波传播过程中,各谐波分量相速不同造成其相 对相位发生变化,引起信号波形变形; • 携带信息的电磁波是具有一定带宽的已调制非单色波, 包络的传播速度才是信号的传递速度 • 非单色波在色散介质中各个单频分量以不同的相速传 播,非单色波携带信号的传递速度是多少? XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

相速与群速 若色散介质中存在两个正旋线极化电磁波: E,=Ecos[(@+△o)1=(P,+△P)] △0<0,△B<<B E2=E,cosI(o,-△o)i(f-△B)] 合成电磁波的场强表达式为 E(t)=E,cos[(o,+△o)t(B+△B)] +E,cos[(o,-△o)1-(f-△Pz] 2E cos(tA@-zAB)cos(@t-Bz) = 角频率o振幅cos(t△Q-Z△)向z方向行进的行波 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 15 相速与群速 若色散介质中存在两个正旋线极化电磁波: 合成电磁波的场强表达式为 10 0 0 20 0 0 cos[( ) ( ) ] cos[( ) ( ) ] EE t z EE t z ωωββ ωωββ = +∆ − +∆ = −∆ − −∆ 0 0 ∆ << ,∆ << ββωω 00 0 00 0 0 0 0 ( ) cos[( ) ( ) ] cos[( ) ( ) ] 2 cos( )cos( ) Et E t z E tz E t z tz ωωββ ωωββ ω β ωβ = +∆ − +∆ + −∆ − −∆ = ∆ −∆ − 角频率ω0振幅cos(t△ω- z△β)向z方向行进的行波 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
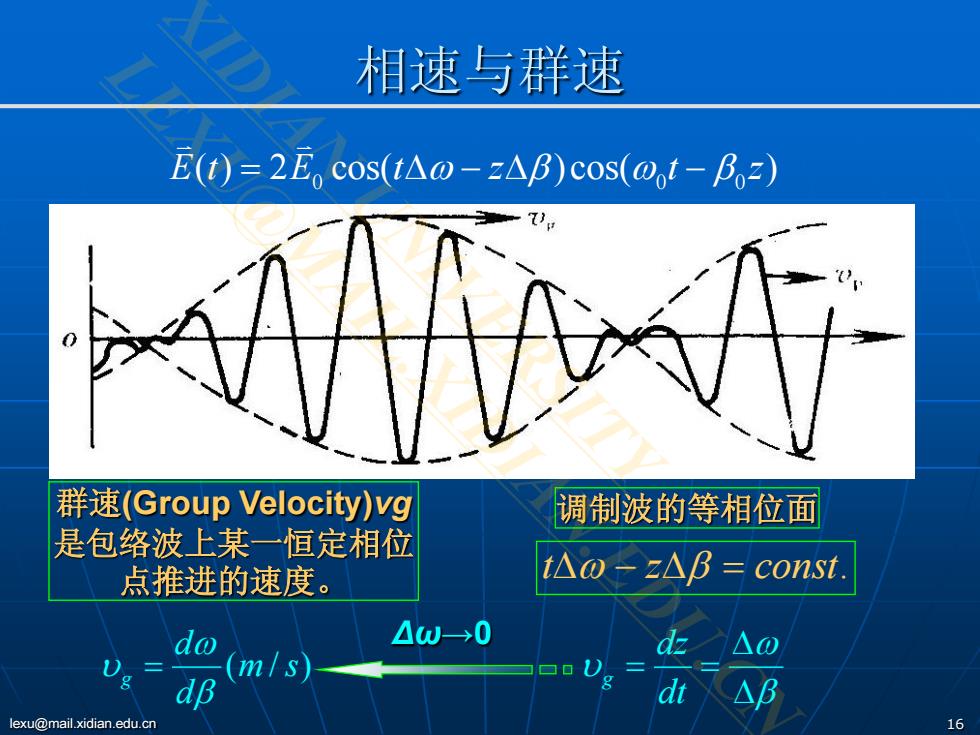
相速与群速 E(t)=2E,cos(t△o-z△B)Cos(0t-P2) 373 群速(Group Velocity)vg 调制波的等相位面 是包络波上某一恒定相位 点推进的速度。 t△ -ZAB const. do △w→0 dz △0 D:= m/s) dB di B lexu@mail.xidian.edu.cn 16
lexu@mail.xidian.edu.cn 16 相速与群速 0 0 0 Et E t z t z ( ) 2 cos( )cos( ) = ∆ −∆ − ω β ωβ 群速(Group Velocity)vg 是包络波上某一恒定相位 点推进的速度。 调制波的等相位面 βω =∆−∆ constzt . β ω υ ∆ ∆ == dt dz g sm )/( d d g β ω υ = Δω→0 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN