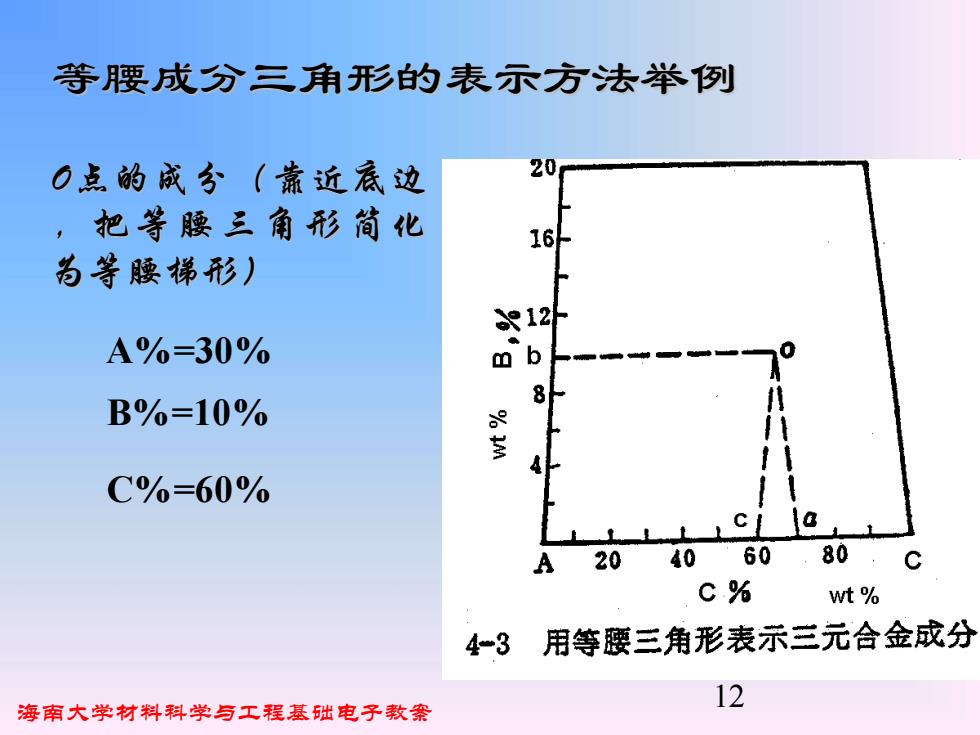
等腰成分三角形的表示方法举例 O点的成分(靠近底边 20 ,把等腰三角形简化 16 为等腰梯形) A%=30% 6 B%=10% C%=60% a 20 4060.80 C% wt 4-3 用等腰三角形表示三元合金成分 海南大学材料科学与工程基础电子教案 12
海南大学材料科学与工程基础电子教案 12 O点的成分(靠近底边 ,把等腰三角形简化 为等腰梯形) A%=30% 等腰成分三角形的表示方法举例 B%=10% C%=60%
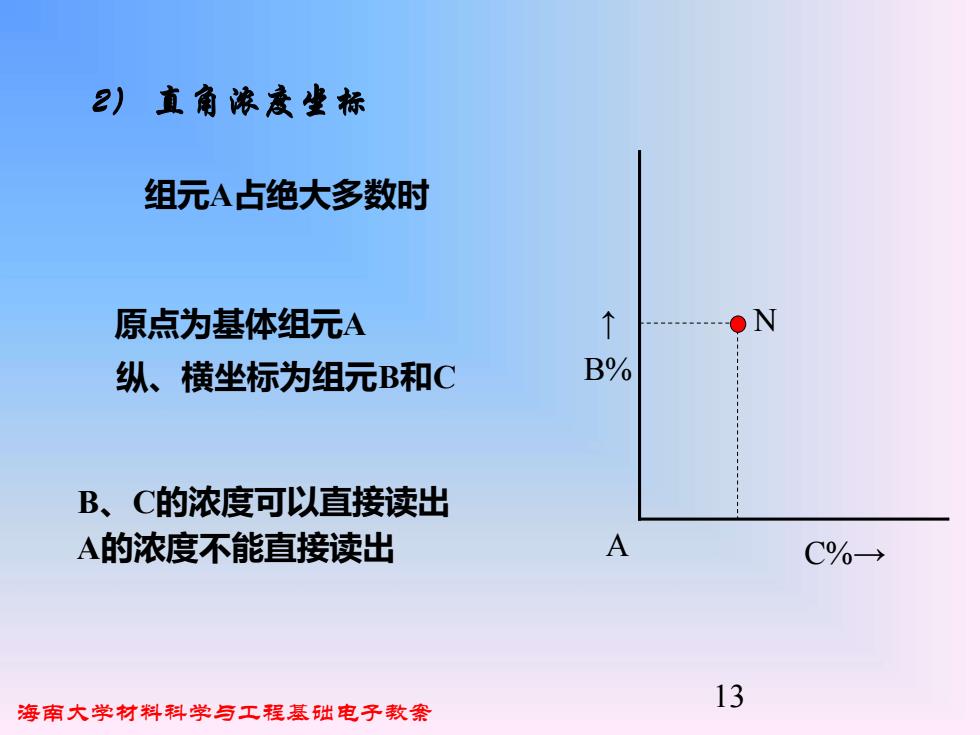
2)直角浓意坐标 组元A占绝大多数时 原点为基体组元A ↑ - 纵、横坐标为组元B和C B% B、C的浓度可以直接读出 A的浓度不能直接读出 A C%→ 海南大学材料科学与工程基础电子教案 13
海南大学材料科学与工程基础电子教案 13 2) 直角浓度坐标 A C%→ ↑ B% 原点为基体组元A 纵、横坐标为组元B和C B、C的浓度可以直接读出 A的浓度不能直接读出 组元A占绝大多数时 N
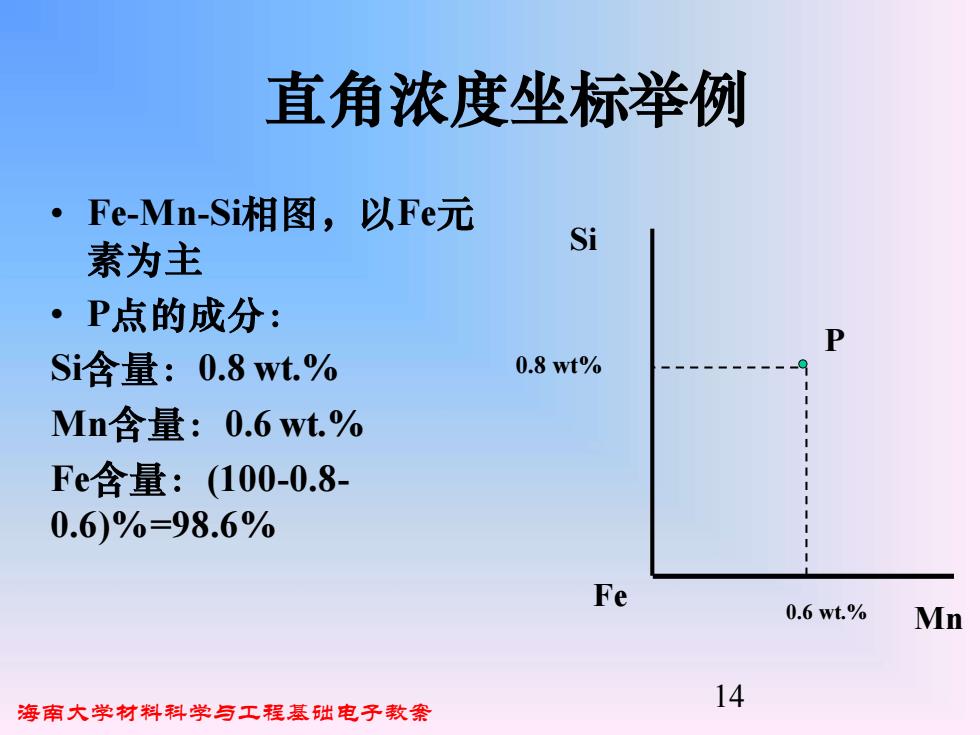
直角浓度坐标举例 Fe-Mn-Si相图,以Fe元 Si 素为主 ·P点的成分: P Si含量:0.8wt% 0.8wt% Mn含量:0.6wt.% Fe含量:(100-0.8- 0.6)%=98.6% Fe 0.6wt.% Mn 海南大学材料科学与工程基础电子教案 14
海南大学材料科学与工程基础电子教案 14 • Fe-Mn-Si相图,以Fe元 素为主 • P点的成分: Si含量:0.8 wt.% Mn含量:0.6 wt.% Fe含量:(100-0.8- 0.6)%=98.6% 直角浓度坐标举例 Fe Si Mn P 0.8 wt% 0.6 wt.%

3)局部图形表示法 研究三元系中一定成分范 围内的材料 B 取出局部加以放大,如、 亚、Ⅲ > I区:合金中三种组元的成分范 围几乎相等; > Ⅱ区:合金中一种组元的成分含 C%o 量较多(A组元); B > Ⅲ区:合金中一种组元的成分变 化不大(A组元),另两种组元 的成分变化比较大(B、C组元) 更加清晰、简单 A ←-A% 15 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 15 3)局部图形表示法 • 研究三元系中一定成分范 围内的材料 • 取出局部加以放大,如I、 II、III ➢ I 区:合金中三种组元的成分范 围几乎相等; ➢ II 区: 合金中一种组元的成分含 量较多(A组元); ➢ III 区:合金中一种组元的成分变 化不大(A组元),另两种组元 的成分变化比较大(B、C组元) • 更加清晰、简单 B A ← C A% B% C% I II III

等边三角形 1、浓度△顶点代表纯组元A、B、C 2、△的边代表二元合金,含有二个 B 组分的组成 AB=BC=CA=100%=边长 WB 3、△内任一点都代表一个三元合金, 含有三个组分的组成 Xa O点合金 WA x2+x+X=100% 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 A B C wC wB wA 1、浓度△顶点代表纯组元A、B、C 2、 △的边代表二元合金,含有二个 组分的组成 AB = BC = CA = 100%=边长 3、 △内任一点都代表一个三元合金, 含有三个组分的组成 O xa xb xc O点合金 xa + xb + xc=100% 等边三角形