
非稳态温度场:温度场内如果各点温度随时间而改变。 t=f(x,y,z,t) 稳态温度场:若温度不随时间而改变。 t=f (x,y,z) 0 稳态一维温度场:若温度场中温度只沿着一个坐标方向变化。 aa t=f(x) 0 02 等温面:温度场中同一时刻相同温度各 法向n 等温面的特点: 等温面 dA (1)等温面不能相交; (2)沿等温面无热量传递。 等温面、温度梯度与热流方向
稳态一维温度场:若温度场中温度只沿着一个坐标方向变化。 t = f (x) 等温面的特点: (1)等温面不能相交; (2)沿等温面无热量传递。 等温面:温度场中同一时刻相同温度各点组成的面。 非稳态温度场:温度场内如果各点温度随时间而改变。 稳态温度场:若温度不随时间而改变。 t=f(x,y,z) t=f(x,y,z,τ) t t t t n t n n dA 法向 等温面 等温面、温度梯度与热流方向 0 t 0 t 0 z t y t
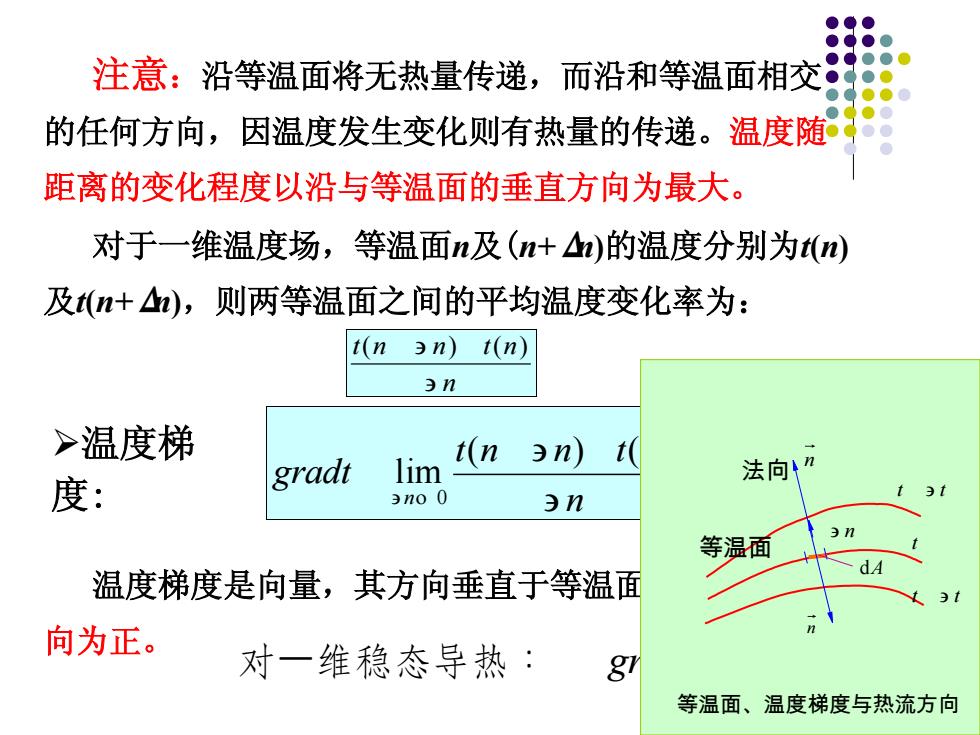
注意:沿等温面将无热量传递,而沿和等温面相交 的任何方向,因温度发生变化则有热量的传递。温度随 距离的变化程度以沿与等温面的垂直方向为最大。 对于一维温度场,等温面n及(n+△n)的温度分别为t(n) 及(+△n),则两等温面之间的平均温度变化率为: (n)n) t(n) 3n >温度梯 lim t(n 3n)t( 法向1n 度: gradt 3n00 3n 3n 等温面 dA 温度梯度是向量,其方向垂直于等温面 向为正。 对一维稳态导热: 8 等温面、温度梯度与热流方向
注意:沿等温面将无热量传递,而沿和等温面相交 的任何方向,因温度发生变化则有热量的传递。温度随 距离的变化程度以沿与等温面的垂直方向为最大。 n t n n t n ( ) ( ) n t n t n n t n gradt n ( ) ( ) lim 0 对于一维温度场,等温面n及(n+Δn)的温度分别为t(n) 及t(n+Δn),则两等温面之间的平均温度变化率为: 温度梯 度: 温度梯度是向量,其方向垂直于等温面,并以温度增加的方 向为正。 dx dt 对一维稳态导热: gradt t t t t n t n n dA 法向 等温面 等温面、温度梯度与热流方向
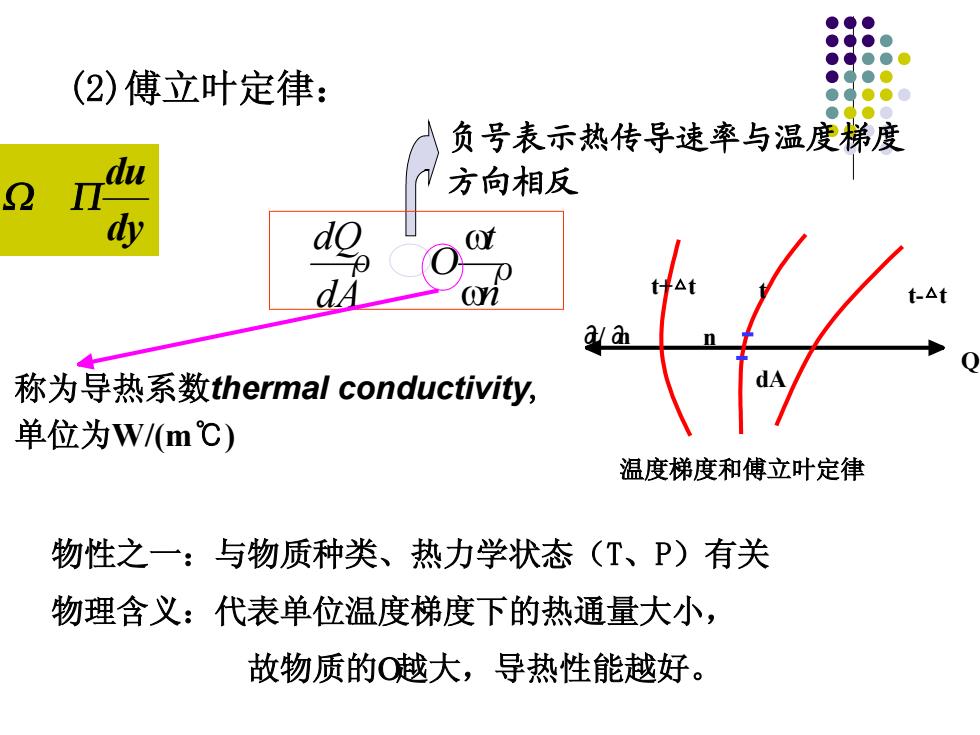
(2)傅立叶定律: 负号表示热传导速率与温度梯度 方向相反 d/a 称为导热系数thermal conductivity,. 单位为Wm℃) 温度梯度和傅立叶定律 物性之一:与物质种类、热力学状态(T、P)有关 物理含义:代表单位温度梯度下的热通量大小, 故物质的©越大,导热性能越好
n t dA dQρ ρ 负号表示热传导速率与温度梯度 方向相反 称为导热系数thermal conductivity, 单位为W/(m℃) 物性之一:与物质种类、热力学状态(T、P)有关 物理含义:代表单位温度梯度下的热通量大小, 故物质的越大,导热性能越好。 (2)傅立叶定律: dy du n dA Q t+△t t t-△t ∂t/∂n 温度梯度和傅立叶定律

导热系数的定义 doldA ot/on 在数值上等于单位温度梯度下的热通量,是物质的物理性质之一 一般,金属的导热系数最大(15一420,W/m℃), 液体(0.1—0.7,W/m℃), 气体(0.006-0.06,W/m℃) 绝热材料(Q,003-0.06,W/m℃) >金属液体〉λ气体 >温度升高时,入液下降(水例外),入气上升, 金属下降,大多入非金属上升
导热系数的定义 t n dQ dA / / 在数值上等于单位温度梯度下的热通量 ,是物质的物理性质之一 一般,金属的导热系数最大(15-420, W / m℃), 液体 (0.1—0.7,W/ m℃), 气体 (0.006-0.06,W/m℃) 绝热材料( 0.003-0.06, W / m℃) λ金属>λ液体>λ气体 温度升高时,λ液 下降(水例外),λ气 上升, λ金属下降,大多λ非金属上升

6.2.2通过平壁的定态导热过程 解决:①温度分布 Q ②热流量 条件:①定态 -6 ②一维(横向导热不计) 分析:①取控制体 ②作热量衡算: 进=出+O dt 定态:累积=0, Q=0 dx dx ③结合特征方程解析解 卡常数时 t A05 积分
6.2.2 通过平壁的定态导热过程 解决:①温度分布 ②热流量 条件:①定态 ②一维(横向导热不计) 分析:①取控制体 ②作热量衡算: 进=出+累积 定态:累积=0, Q1=Q ③结合特征方程解析解 λ=常数时 积分 温度分布 线性, dx dt q A Q t t x dx dt A Q 0 1 x A Q t t 1 1 2 t t Q A