《大学物理》课程教学资源（教案讲义）ch2 牛顿运动定律与力学中的守恒定律

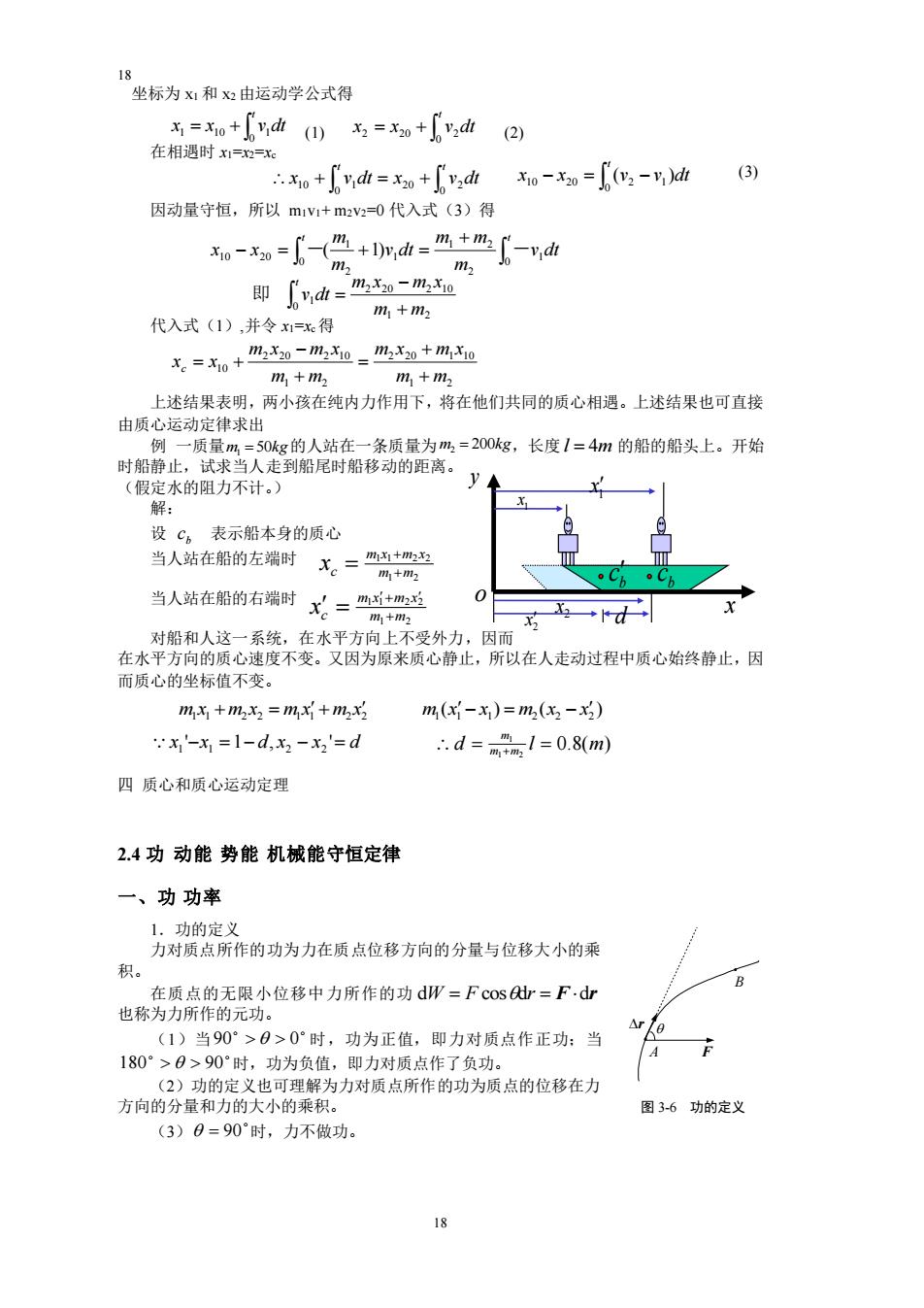
18 坐标为x1和x2由运动学公式得 =x0+dt (1)=x20+vadt (2) 在相遇时==x o+=x+=(v2-v )dr (3) 因动量守恒，所以mv1+m2v2=0代入式(3)得 -=【-侣+wh=%+-h m 即d=%-me 代入式(1)，并令=x得 m+mz 气=和+他二m.+m m+mz m+m 上述结果表明，两小孩在纯内力作用下，将在他们共同的质心相遇。上述结果也可直接 由质心运动定律求出 例一质量m=50kg的人站在一条质量为m,=200kg,长度1=4m的船的船头上。开始 时船静止，试求当人走到船尾时船移动的距离。 (假定水的阻力不计。) 解： 设C。表示船本身的质心 当人站在船的左端时 术。=m+ +m 当人站在船的右端时X。=丝 对船和人这一系统，在水平方向上不受外力，因而 。一 在水平方向的质心速度不变。又因为原来质心静止，所以在人走动过程中质心始终静止，因 而质心的坐标值不变。 m名+m2=m+m2X m(-x)=m(3-) x'-x1=1-d,x2-2'=d d=1=0.8m 四质心和质心运动定理 2.4功动能势能机械能守恒定律 一、功功率 力条的功内力在质点位的分量与移大小的采 也称秀限个位移中力所作的功=Fs仙=F,山 4)当90>0>0时，功为正值，即力对质点作正功：当 180>0>90时，功为负值，即力对质点作了负功. 方向的分量方力对质点所作的功为黄的修在力 图36功的定义 (3)0=90°时，力不做功。 学

18 18 o 1 x  1 x 2 x  2 x d x y b c b c  坐标为 x1 和 x2 由运动学公式得 (1) (2) 在相遇时 x1=x2=xc (3) 因动量守恒，所以 m1v1+ m2v2=0 代入式（3）得 代入式（1）,并令 x1=xc得 上述结果表明，两小孩在纯内力作用下，将在他们共同的质心相遇。上述结果也可直接 由质心运动定律求出 例 一质量 的人站在一条质量为 ，长度 的船的船头上。开始 时船静止，试求当人走到船尾时船移动的距离。 （假定水的阻力不计。） 解： 设 b c 表示船本身的质心 当人站在船的左端时 当人站在船的右端时 对船和人这一系统，在水平方向上不受外力，因而 在水平方向的质心速度不变。又因为原来质心静止，所以在人走动过程中质心始终静止，因 而质心的坐标值不变。 x1 '−x1 =1− d, x2 − x2 ' = d 四 质心和质心运动定理 2.4 功 动能 势能 机械能守恒定律 一、功 功率 1．功的定义 力对质点所作的功为力在质点位移方向的分量与位移大小的乘 积。 在质点的无限小位移中力所作的功 dW = F cosdr = F dr 也称为力所作的元功。 （1）当   90    0 时，功为正值，即力对质点作正功；当   180    90 时，功为负值，即力对质点作了负功。 （2）功的定义也可理解为力对质点所作的功为质点的位移在力 方向的分量和力的大小的乘积。 图 3-6 功的定义 （3）   = 90 时，力不做功。  A F B r  = + t x x v dt 0 1 10 1  = + t x x v dt 0 2 20 2    + = + t t x v dt x v dt 0 20 2 0 10 1  − = − t x x v v dt 0 10 20 2 1 ( )   + − = + = t t v dt m m m v dt m m x x 0 1 2 1 2 0 1 2 1 10 20 －( 1) － 1 2 2 20 2 10 0 1 m m m x m x v dt t + − = 即  1 2 2 20 1 10 1 2 2 20 2 10 10 m m m x m x m m m x m x x x c + + = + − = + m1 = 50kg m2 = 200kg l = 4m 1 2 1 1 2 2 m m m x m x c x + + = 1 2 1 1 2 2 m m m x m x c x +  +   = 1 1 2 2 1 1 2 2 m x +m x = m x  +m x  ( ) ( ) 1 1 1 2 2 2 m x  − x = m x − x  0.8( ) 1 2 d m 1 m l m m  = = +

(4)功是标量。只有大小，没有方向。 2.变力作功W=∫dW=∫F.d=Fcos，F=F,i+F,j+Fk, dr dxi+dyj+dzk. 在直角坐标系中，W=F.dr=(Fdr+F,dy+Fd) 3.合力的功 根据力的叠加原理F=F+F2+F+.,合力的功为 W=[F.dr=F+F+F+.).dr=W+W+W;+. 即合力对质点所作的功，等于每个分力所作的功的代数和。 一对相互作用力的功与参考系无关。 冬功单位：焦耳O,Nm 动流时的支化率，P-晋亦P-晋=Fcas0出P=s8,平药动 dt 率为 P=形 t 功率单位：瓦特(W). 二、动能定理 力对质点做功，其效果是使质点的运动状态发生变化。质点动能定理正是反映力做功与 质点运动状态变化之间的关系： 由牛顿第二定律及切向加速度的定义得 dW=F.dr=Fcosair Fca0=ma=m出 dw=mg=mt。 积分可得合外力的功为 形=md=m-2m. 图37动能定理 1.动能的定义 E=m. 2.质点的动能定理W=E2-E1,合外力对质点所作的功，等于质点动能的增量。 3.讨论 (1)动能Ek是标量，仅是状态量v的单值函数，它是状态量： 与动能的本质区别：它们的单位和量纲相同，但功是过程量，动能：是状态量： 动能定理牛第二定律号出，只适用于性参考系，并且动能也与参考系有 意义 关。 (5)由质点的动能定理可知，当合外力做正功时，质点的动能增加：当合外力做负功 时，质点的动能减少。亦即质点反抗外力做功是以自身动能的减少为代价，可见动能是质点 因运动而具有的做功本领。 (6)动能定理的表达式是一个标量方程，它只涉及质点运动的初态和终态，不问运动

19 19 （4）功是标量。只有大小，没有方向。 2 ． 变 力 作 功    = =  = B A B A W dW F dr F cosdr ， F = Fx i + Fy j + Fz k ， dr = dxi + dyj + dzk . 在直角坐标系中，   =  = + + B A x y z B A W F dr (F dx F dy F dz). 3．合力的功 根据力的叠加原理 F = F1 + F2 + F3 +. 合力的功为 W =  d =  ( 1 + 2 + 3 +)d =W1 +W2 +W3 + B A B A F r F F F r 即合力对质点所作的功，等于每个分力所作的功的代数和。 一对相互作用力的功与参考系无关。 4．功的单位：焦耳（J），1J=N·m 5．功率 功随时间的变化率， t W P d d = . 亦即 t r F t W P d d cos d d = =  . ∴ P = Fv cos ，平均功 率为 t W P = ， 功率单位：瓦特（W）. 二、动能定理 力对质点做功，其效果是使质点的运动状态发生变化。质点动能定理正是反映力做功与 质点运动状态变化之间的关系。 由牛顿第二定律及切向加速度的定义得： dW = F dr = F cosdr ， t v F ma m d d cos =  = ， r mv v t v W m d d d d d = = . 积分可得合外力的功为 2 1 2 2 2 1 2 1 d 2 1 W mv v mv mv v v = = −  . 1．动能的定义 2 2 1 E mv k = . 2．质点的动能定理 W = Ek 2 − Ek1，合外力对质点所作的功，等于质点动能的增量。 3．讨论 （1）动能 Ek 是标量，仅是状态量 v 的单值函数，它是状态量； （2）功与动能的本质区别：它们的单位和量纲相同，但功是过程量，动能 Ek 是状态量； 功是能量变化的量度； （3）功和能具有普遍意义； （4）动能定理由牛顿第二定律导出，只适用于惯性参考系，并且动能 Ek 也与参考系有 关。 （5）由质点的动能定理可知，当合外力做正功时，质点的动能增加；当合外力做负功 时，质点的动能减少。亦即质点反抗外力做功是以自身动能的减少为代价，可见动能是质点 因运动而具有的做功本领。 （6）动能定理的表达式是一个标量方程，它只涉及质点运动的初态和终态，不问运动 a v a dr v F b v b 图 3-7 动能定理

0 过程的细节，因此，在求解某些力学问题时比较方便。 【例3】一质量为m的小球系在长为1的细绳下端，绳的上端固定在天花板上。起初 把绳子放在与铅直线成日。角处，然后放手使小球沿圆弧下落。试求绳与铅直线成0角时， 小球的速 【解】（第一步：计算外力所作的功）小球受力如图3-8所示。由分析可知为变力作 功W=广Fd山=广Tdr+广P.d山，因为广Td=0和 [P.dr=[Pcos dr=[Psin air 并且注意到dr=-ld0,因此 W=[mg sin ar=-mgl sin =mgl(cos0-cos) (第二步：用动能定理求小球的速度) 由动能定理，得 W-mgl(cos0-cos0,)=mmm. 故绳与铅直线成0角时，小球的速率为v=√2g(cos0-cos). 例题2-10装有货物的木箱，重G=980N,要把它运上汽车。现将长1=3m的木板搁在汽车 后部，构成一斜面，然后把木箱沿斜面拉上汽车。斜面与地面成30角，木箱与斜面间的滑 绳的拉力与料面成10°用 小、为700N如图 (1)木 面对木箱的支持力N 7777777 (1)拉力F所做的功A1 重力所清的知10=70x3x085/=207x10/ -60)=980×3×(-0.5)J=-1.47×103J 摩擦力所作的功A:分析木箱的受力，由于木箱在垂直于斜面方向上没有运动，根据 牛顿第二定律得 W+Fsin 10°-Gcos30°=0 N=Gcos30°-Fsim10°=727N 由此可求得摩擦力f=W=0.20×727N=145N A,=f1cos180°=-145×3J=-435J 因为重力和摩擦力在这里是阻碍物体运动的力，所以它们对物体所作的功都是负值

20 20 过程的细节，因此，在求解某些力学问题时比较方便。 【例 3】 一质量为 m 的小球系在长为 l 的细绳下端，绳的上端固定在天花板上。起初 把绳子放在与铅直线成  0 角处，然后放手使小球沿圆弧下落。试求绳与铅直线成  角时， 小球的速率。 【解】 （第一步：计算外力所作的功）小球受力如图 3-8 所示。由分析可知为变力作 功    =  =  +  r r r F r T r P r 0 0 0 d d d r r r W ， 因 为 d 0 0  =  r T r r 和     = = r r r r r P r P r 0 0 0 d cosd sin d r P r ， 并且注意到 dr = −ld ，因此 sin d sin d (cos cos ) 0 0 0        = = − = − W  mg r  mgl mgl r r . （第二步：用动能定理求小球的速度） 由动能定理，得 2 2 0 2 0 2 1 2 1 2 1 W = mgl(cos − cos ) = mv − mv = mv . 故绳与铅直线成  角时，小球的速率为 2 (cos cos ) = gl  − 0 v . 例题 2-10 装有货物的木箱，重 G＝980N，要把它运上汽车。现将长 l＝3m 的木板搁在汽车 后部，构成一斜面，然后把木箱沿斜面拉上汽车。斜面与地面成 30o 角，木箱与斜面间的滑 动摩擦系数 =0.20， 绳的拉力 与斜面 成 10o 角，大小 为 700N，如 图 (a) 所示。 求：（1）木箱所受各力所作的功；（2）合外力对木箱所作的功；（3）如改用起重机把木箱直 接吊上汽车能不能少做些功？ 解： 木箱所受的力为：拉力 F ，方向与斜面成 100 角向上；重力 G ，方向竖直向下；斜 面对木箱的支持力 N ，方向垂直于斜面向上，斜面对木箱的摩擦力 f 方向和斜面平行，与 木箱运动方向相反，如图 (b).已知 l=3m,每个力所作的功可计算如下。 （1）拉力 F 所做的功 A1 重力所做的功 A2 正压力所做的功 A3 摩擦力所作的功 A4；分析木箱的受力，由于木箱在垂直于斜面方向上没有运动，根据 牛顿第二定律得 由此可求得摩擦力 因为重力和摩擦力在这里是阻碍物体运动的力，所以它们对物体所作的功都是负值。  0  l  T dr  P O A Fl J J 3 1 = cos10 = 70030.985 = 2.0710  A Fl J J 3 2 = cos（180 －60 ）= 9803（－0.5） =－1.4710   3 = cos90 = 0  A Nl + sin10 − cos30 = 0   N F G N Gcos30 F sin10 = 727N ＝ －  f r = N = 0.20727N =145N A f l J J 4 r cos180 = −1453 = −435 ＝    F F f r G N  