
Performance Impact of Control Divergence Boundary condition checks are vital for complete functionality and robustness of parallel code The tiled matrix multiplication kernel has many boundary condition checks The concern is that these checks may cause significant performance degradation For example,see the tile loading code below: if(Row Width &p TILE WIDTH+tx Width){ ds_M[ty][tx]M[Row Width p TILE_WIDTH tx]; else ds_M[ty][tx]=0.0; 3 if (p*TILE_WIDTH+ty Width &Col Width){ ds_N[ty][tx]N[(p*TILE_WIDTH ty)Width Col]; else ds_N[ty][tx]=0.0; 电子神越女学 O
16 Performance Impact of Control Divergence – Boundary condition checks are vital for complete functionality and robustness of parallel code – The tiled matrix multiplication kernel has many boundary condition checks – The concern is that these checks may cause significant performance degradation – For example, see the tile loading code below: if(Row < Width && p * TILE_WIDTH+tx < Width) { ds_M[ty][tx] = M[Row * Width + p * TILE_WIDTH + tx]; } else { ds_M[ty][tx] = 0.0; } if (p*TILE_WIDTH+ty < Width && Col < Width) { ds_N[ty][tx] = N[(p*TILE_WIDTH + ty) * Width + Col]; } else { ds_N[ty][tx] = 0.0; }
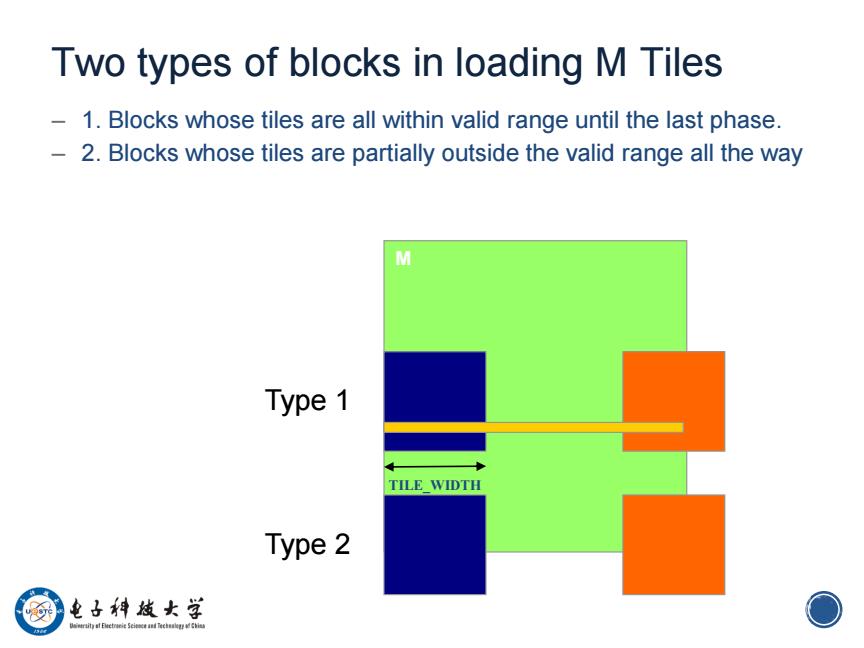
Two types of blocks in loading M Tiles 1.Blocks whose tiles are all within valid range until the last phase. 2.Blocks whose tiles are partially outside the valid range all the way Type 1 TILE_WIDTH Type 2 电子科妓女学 O
17 Two types of blocks in loading M Tiles – 1. Blocks whose tiles are all within valid range until the last phase. – 2. Blocks whose tiles are partially outside the valid range all the way M TILE_WIDTH Type 1 Type 2

Analysis of Control Divergence Impact -Assume 16x16 tiles and thread blocks Each thread block has 8 warps(256/32) Assume square matrices of 100x100 Each thread will go through 7 phases(ceiling of 100/16) There are 49 thread blocks (7 in each dimension) 电子科妓女学 O
18 Analysis of Control Divergence Impact – Assume 16x16 tiles and thread blocks – Each thread block has 8 warps (256/32) – Assume square matrices of 100x100 – Each thread will go through 7 phases (ceiling of 100/16) – There are 49 thread blocks (7 in each dimension)

Control Divergence in Loading M Tiles Assume 16x16 tiles and thread blocks -Each thread block has 8 warps(256/32) Assume square matrices of 100x100 Each warp will go through 7 phases(ceiling of 100/16) There are 42(6*7)Type 1 blocks,with a total of 336(8*42)warps They all have 7 phases,so there are 2,352(336*7)warp-phases The warps have control divergence only in their last phase 336 warp-phases have control divergence M Type 1 TILE WIDTH 电子神越女学
19 Control Divergence in Loading M Tiles – Assume 16x16 tiles and thread blocks – Each thread block has 8 warps (256/32) – Assume square matrices of 100x100 – Each warp will go through 7 phases (ceiling of 100/16) – There are 42 (6*7) Type 1 blocks, with a total of 336 (8*42) warps – They all have 7 phases, so there are 2,352 (336*7) warp-phases – The warps have control divergence only in their last phase – 336 warp-phases have control divergence

Control Divergence in Loading M Tiles (Type 2) Type 2:the 7 block assigned to load the bottom tiles,with a total of 56 (8*7)warps They all have 7 phases,so there are 392(56*7)warp-phases The first 2 warps in each Type 2 block will stay within the valid range until the last phase The 6 remaining warps stay outside the valid range So,only 14(2*7)warp-phases have control divergence TILE WIDTH 电子科妓女学 Type 2
20 Control Divergence in Loading M Tiles (Type 2) – Type 2: the 7 block assigned to load the bottom tiles, with a total of 56 (8*7) warps – They all have 7 phases, so there are 392 (56*7) warp-phases – The first 2 warps in each Type 2 block will stay within the valid range until the last phase – The 6 remaining warps stay outside the valid range – So, only 14 (2*7) warp-phases have control divergence