
Random numbers,general distribution 3)Special PDFs:Directly use the definition of the distribution. For example,binomial random numbers.A binomial random number is the number of heads in N tosses of a coin with probability of a heads on any single toss.If you generate uniform random numbers on the interval (0,1)and count the number less than p,then the count is a binomial random number with parameters N and p. This function is a simple implementation of a binomial RNG using the direct approach: functionX directbinornd(N,p,m,n) X zeros(m,n);Preallocate memory for i=1:m*n u rand(N,1); X(i)=sum(u p); end end
3)Special PDFs: Directly use the definition of the distribution. For example, binomial random numbers. A binomial random number is the number of heads in N tosses of a coin with probability of a heads on any single toss. If you generate uniform random numbers on the interval (0,1) and count the number less than p, then the count is a binomial random number with parameters N and p. This function is a simple implementation of a binomial RNG using the direct approach: functionX = directbinornd(N,p,m,n) X = zeros(m,n); % Preallocate memory for i = 1:m*n u = rand(N,1); X(i) = sum(u < p); end end
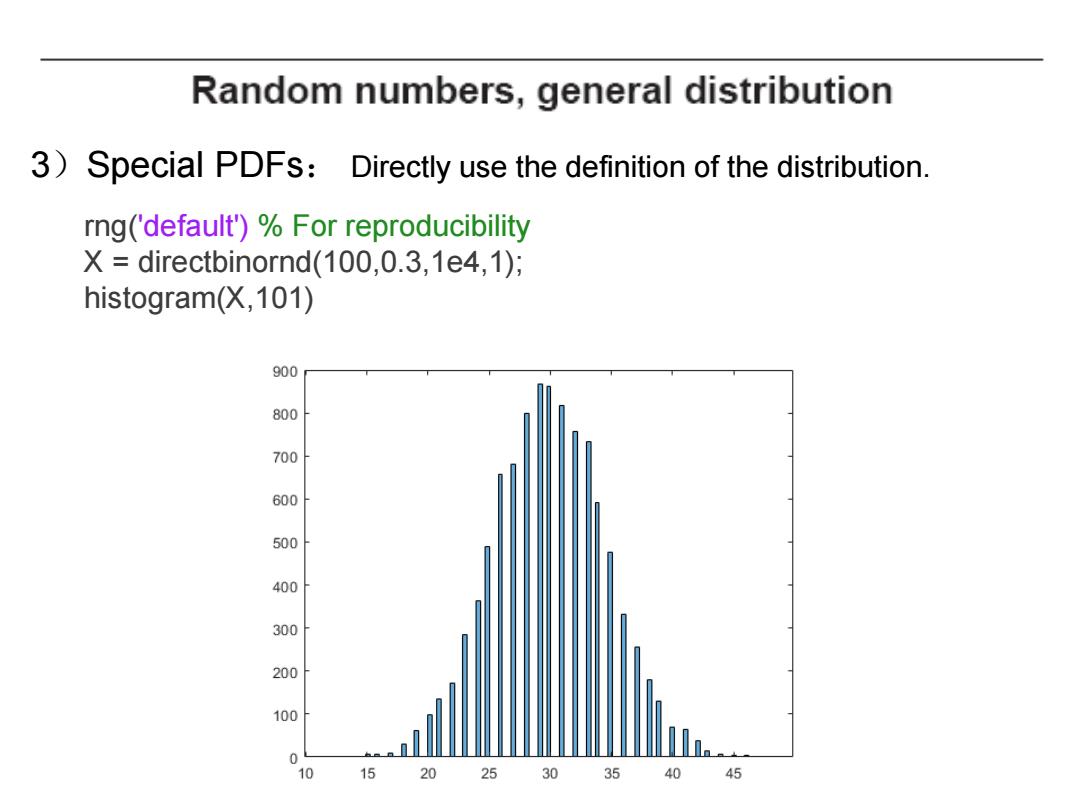
Random numbers,general distribution 3)Special PDFs:Directly use the definition of the distribution. rng('default')%For reproducibility X directbinornd(100,0.3,1e4,1); histogram(X,101) 900 800 700 600 500 400 300 200 100 0 0 15 20 25303540 45
3)Special PDFs: Directly use the definition of the distribution. rng('default') % For reproducibility X = directbinornd(100,0.3,1e4,1); histogram(X,101)

Random numbers,general distribution 2. Inversion Method: Based on the observation that continuous CDFs range uniformly over the interval (0,1).If U is a uniform random number on (0,1), then using X=F-1(U)generates a random number X from a continuous distribution with x specified CDFs F. Simple > Easy to program Widely used Strategy:try to transform F to another distribution,such that inverse of new F is explicitly known
Strategy: try to transform F to another distribution, such that inverse of new F is explicitly known. 2. Inversion Method: Based on the observation that continuous CDFs range uniformly over the interval (0,1). If U is a uniform random number on (0,1), then using X=F-1(U) generates a random number X from a continuous distribution with x specified CDFs F. Simple Easy to program Widely used
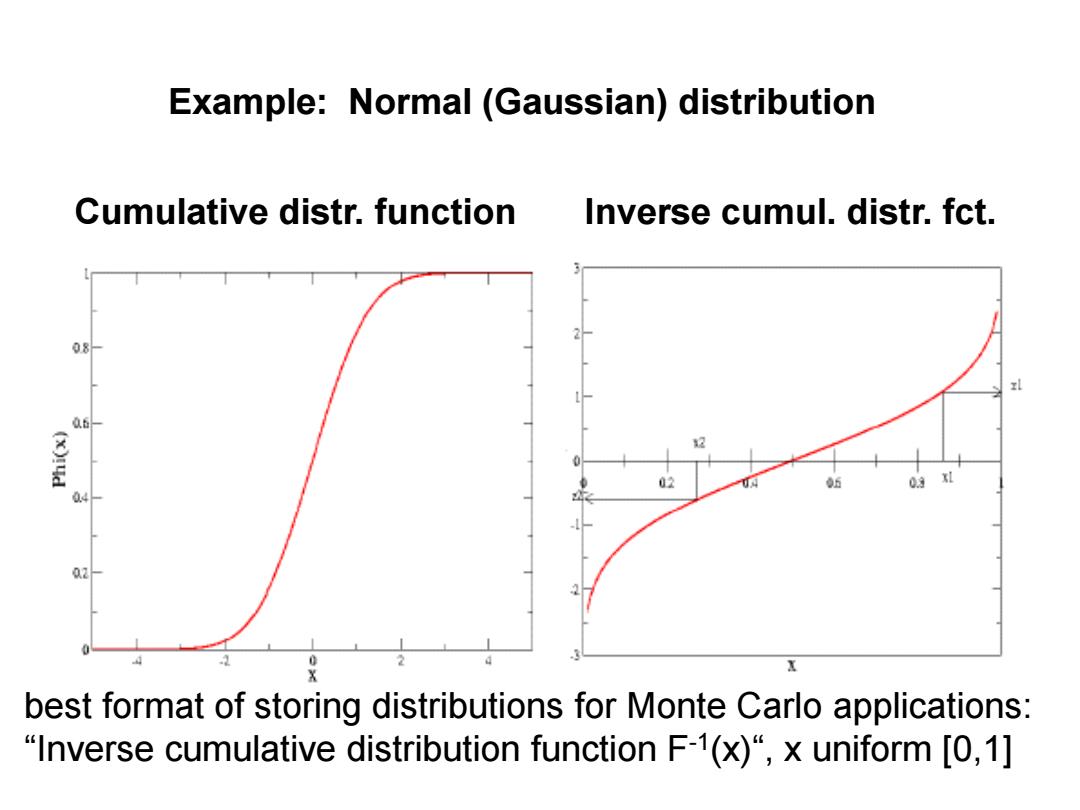
Example:Normal (Gaussian)distribution Cumulative distr.function Inverse cumul.distr.fct. 08 ab- 02 95 0.4 X best format of storing distributions for Monte Carlo applications: "Inverse cumulative distribution function F-1(x)",x uniform [0,1]
Example: Normal (Gaussian) distribution Cumulative distr. function Inverse cumul. distr. fct. best format of storing distributions for Monte Carlo applications: “Inverse cumulative distribution function F-1(x)“, x uniform [0,1]

Random numbers,general distribution 2. Inversion Method: For example,the following code generates random numbers f from a specific Exponential Distribution using the inverse CDF and the uniform random number generator rand: rng('default)%For reproducibility mu=1; X expinv(rand(1e4,1),mu); 1800 1600 1400 1200 1000 800 600 400 200
2. Inversion Method: For example, the following code generates random numbers from a specific Exponential Distribution using the inverse CDF and the uniform random number generator rand: rng('default') % For reproducibility mu = 1; X = expinv(rand(1e4,1),mu);