
2 [「8+鼎 11 K=盟 k盟+盟82 (q) k货 编+k」3 这就是忽略轴向变形的矩形刚架的结构刚度矩阵。于是,式(P)可简写为 KA=P (12-18) 解得 4=K1P (12-19) 考察式(q)的结构刚度矩阵K可知,形成忽略轴向变形的矩形刚架的结构刚度矩阵,同样符 合“对号入座”规则。 用直接刚度法形成忽略轴向变形的矩形刚架的结构刚度矩阵,同样应先通过单元定位向量 对单元刚度矩阵进行“换码”,确定各单元刚度矩阵各个元素在结构刚度矩阵中的位置,据此将单 元刚度矩阵中各元素送到结构刚度矩阵中“对号人座”。值得指出,利用单元定位向量对单元刚 度矩阵进行“换码”时,各单元的定位向量与单元的局部坐标系的选释有关,如果采用式(12-8) 所表示的单元刚度矩阵,则竖柱单元的上端应为始端(即;端),下端应为末端(即j端),这一点 应特别注意。 对于本例,各单元的定位向量为 m=[1200]r, 1a=[0203,1=[1300] 对于图12-8a所示结构,若1=12=1,El1=E1,E2=2E1,将其代入式()、(1)、(n)及式 (q)可得结构刚度矩阵为

123 249g1 2型42 则 「扇克 K克烈 茶 -克 当刚架上的结点荷载F1=0,F2=F,M1=M2=Fl时,则有 P=[F+F2 M M2J=[F Fl Fpl] 将P及K'代人式(12-19)有 希e 一克 「始 城 5 品 别 5 求得刚架结点位移后,根据前述单元定位向量可将单元杆端位移取为相应的结点位移,则可 由单元刚度方程求得单元杆端力。 单元:4,400r=600 吧 T0.50F, 票 -6 型 0.308F 吧 -0.50F M 型 鳄 或 o 0.192Fn4 单元②:8=[04104,J=[0 甜0 (F 「架 票 -24 9 10 1.385Fe 0.692F 9 - 架 0 1.385F M 0.692F,1
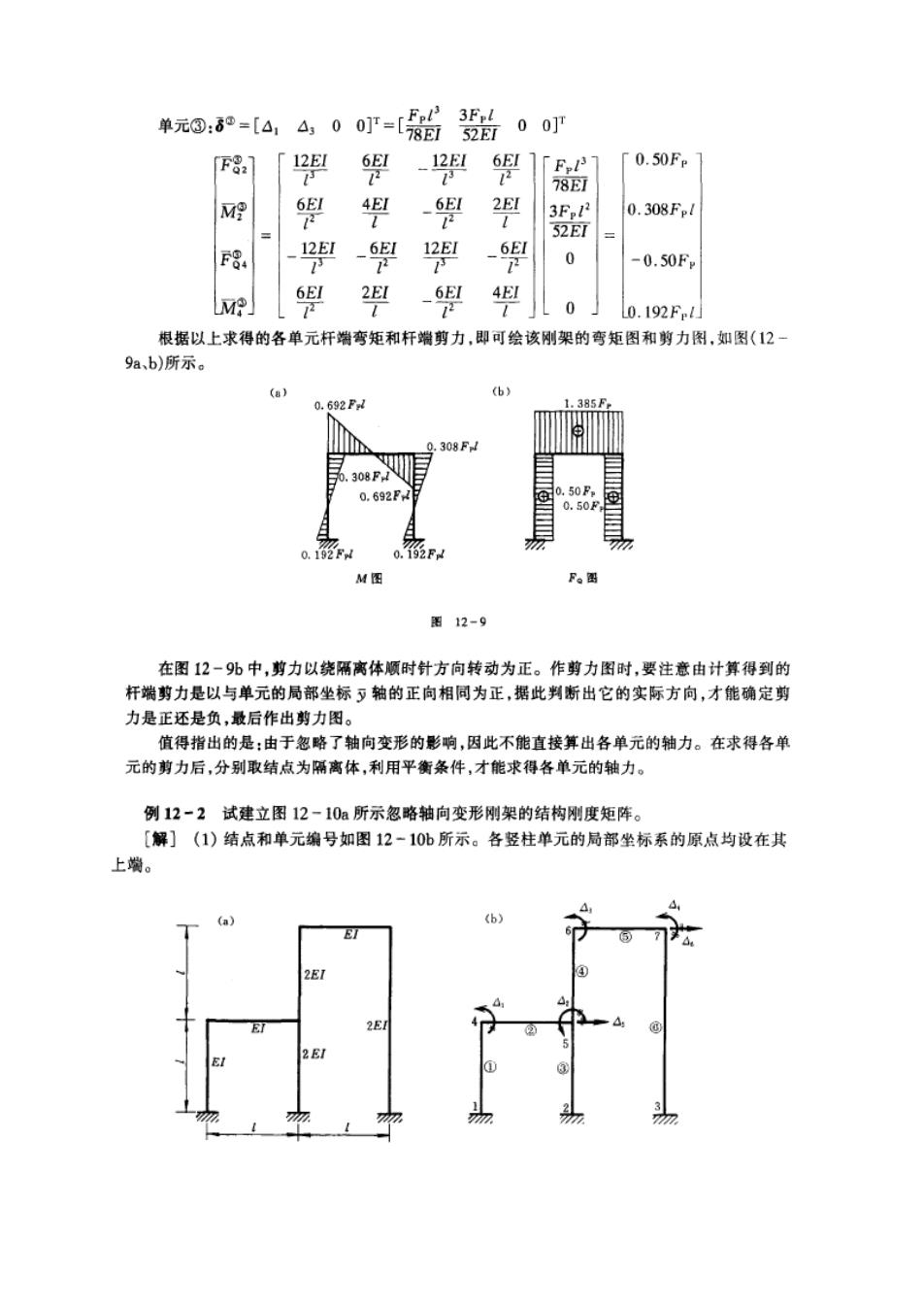
单元@:6=[44,00r=65000r F8: 「g 9-哭 1「 0.50Fm M 興 0.308Fm 0 -0.50F M 0 0.192F.1 根据以上求得的各单元杆端弯矩和杆端剪力,即可绘该刚架的弯矩图和剪力图,如图(12 9a,b)所示。 (a) (b】 .692P M图 F图 0图12-9 在图12-9%中,剪力以绕隔离体顺时针方向转动为正。作剪力图时,要注意由计算得到的 杆端剪力是以与单元的局部坐标夕轴的正向相同为正,据此判断出它的实际方向,才能确定剪 力是正还是负,最后作出剪力图。 值得指出的是:由于忽略了轴向变形的影响,因此不能直接算出各单元的轴力。在求得各单 元的剪力后,分别取结点为隔离体,利用平衡条件,才能求得各单元的轴力。 例12-2试建立图12-10a所示忽略轴向变形刚架的结构刚度矩阵。 解](1)结点和单元编号如图12-10b所示。各竖柱单元的局部坐标系的原点均设在其 上端