
相应的结点荷载列向量为: P=[-605030]rkN·m 图12-6 列出各单元定位向量,建立各单元刚度矩阵并按定位向量进行换码,可得单元①: 2"=[01 「4(0.75E)2(0.75E70 6 20.75En40.75ED1 (b) 0 单元②: 0=[12] D21 1 2 8 「0.75E10.375EI11 21$En41E2l0.ns日0.5E2 (c) 8 8 单元③: 1=[23] 3 0= 喂2 r0.667E10.333EI12 0.333E10.667E】3 (d) 对上述三个单元刚度矩阵中的各元素,按其行码和列码直接送人结构刚度矩阵中, 进行“对号人座”,可得 2 1 2 3 [(0.5EI+0.75E) 0.375EI 011「1.250.375011 K 0.375E (0.75E1+0.667E1)0.333E12=E10.3751.4170.3332 0 0.333E1 0.667E3 0.3330.6673
相应的结点荷载列向量为: 列出各单元定位向量,建立各单元刚度矩阵并按定位向量进行换码,可得单元① : 单元②: 单元③ : 对上述三个单元刚度矩阵中的各元素,按其行码和列码直接送人结构刚度矩阵中, 进行“对号人座”,可得 则

「0.879 -0.2640.132 K1=-0.26 0.879 -0.439 (e) L0.132 -0.439 1.718 将式(a)和式(e)代入式(12-17),求得结点角位移为 f47 「0.879 -0.264 0.1327「-60 「-61.98 4=-0.264 0.879 -0.439 30×10=946.62 IA. L0.132-0.4391.718JL30J L21.67 根据所得的结点角位移,并分别利用式(b)、(c)()的三个单元刚度矩阵,可求得各单元的 杆端弯矩为 单元①: 9=0,9=4,=-61810 [M1「0.5Er0.25E7「07 「-15.50 「-15.50 ×103Nm= kN.m L-31.001 -31.0m 单元②: 9=4=-618X10, p9=4,=46.62x10 M]「0.75E0.375E1-6198 「-29.00 「-29.00 ×10= ×10Nm= kN'm Mg」 0.375E10.75EJ46 11.70 11.70 单元③: p°=42=46.62X10 =4,=21.67×10 0.667E1 0.33E2] 38.30 38.30 ×10= ×10Nm= kN.m gn.383BI0.67E2E 30.00 30.00 利用上述各单元的杆端弯矩,按照弯矩图应画在受拉一侧的原则绘制结构的弯矩图,如困 12-7所示。 29.0 M图(单位kN·m】 图12-7 值得注意的是,由于本章对杆端力符号的规定与位移法及材料力学都不同,所以在作M图 时应注意弯矩对杆端是以逆时针方向为正,从正确判断受拉的 最后,对计算结果进行校核,即取结点2,3,4为隔离体,分别验证其力矩平衡条件,得知全部 满足,故计算结果无误
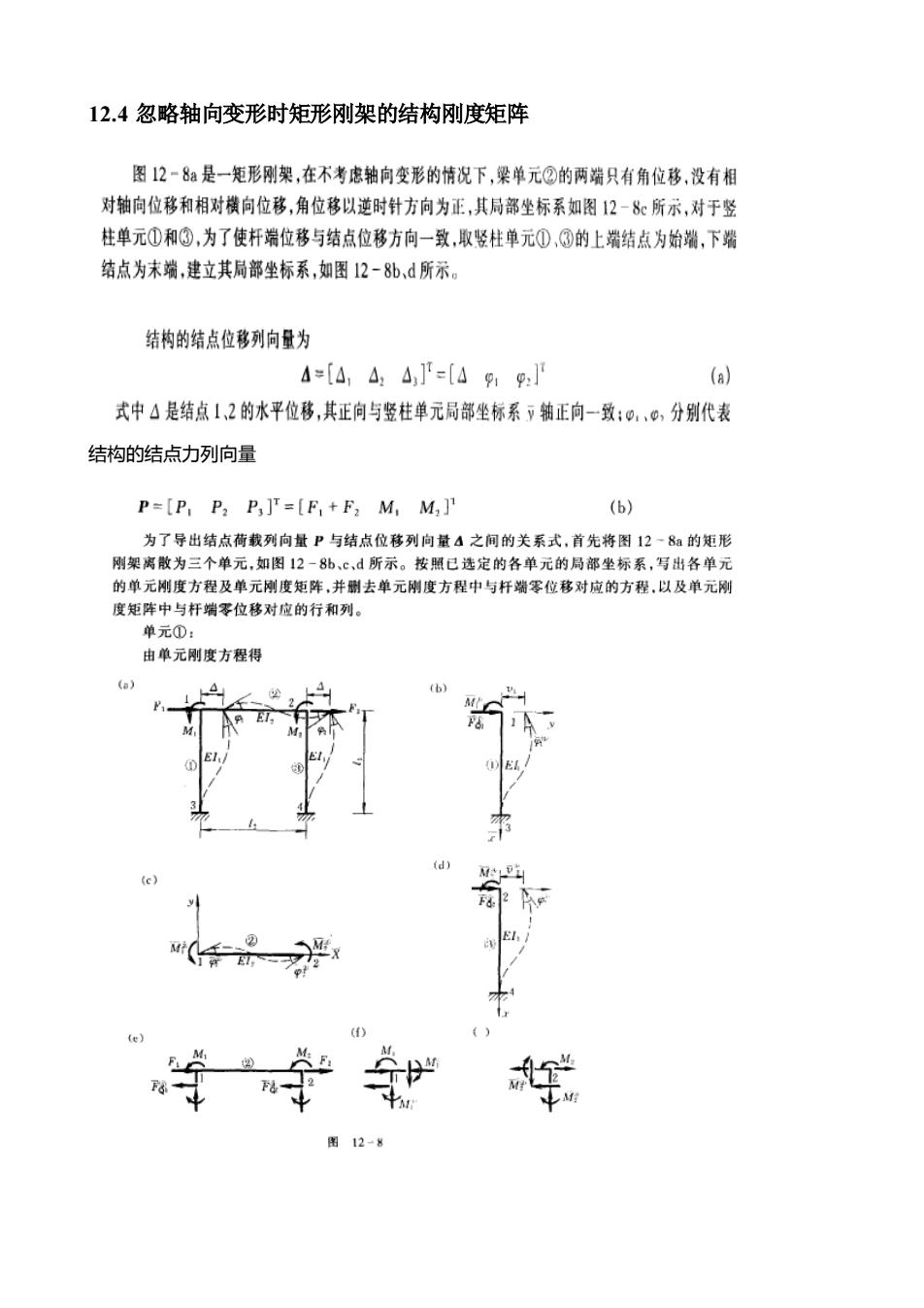
12.4忽略轴向变形时矩形刚架的结构刚度矩阵 图12-8a是一矩形刚架,在不考虑轴向变形的情况下,梁单元②的两端只有角位移,没有相 对轴向位移和相对横向位移,角位移以逆时针方向为正,其局部坐标系如图12-8所示,对于竖 柱单元①和③,为了使杆端位移与结点位移方向一致,取竖柱单元0,③的上端结点为始端,下州 结点为末端,建立其局部坐标系,如图12-8b,d所示。 结构的结点位移列向量为 4=[4,44]=[ag,j () 式中△是结点,2的水平位移,其正向与竖柱单元局部坐标系,轴正向一致:,心,分别代表 结构的结点力列向量 P=[P,P:P]=[F,+F2 M.M] (b) 为了导出结点荷载列向量P与结点位移列向量4之间的关系式,首先将图12~8的矩形 刚架离散为三个单元,如图12-8b:©,d所示。按照已选定的各单元的局部坐标系,写出各单元 的单元刚度方程及单元刚度矩阵,并酬去单元刚度方程中与杆端零位移对应的方程,以及单元刚 度矩阵中与杆端零位移对应的行和列。 单元①: 由单元刚度方程得
12.4 忽略轴向变形时矩形刚架的结构刚度矩阵 结构的结点力列向量

(e) 由单元刚度矩阵得: [12EL 6EL:F 6E1, 4El L M 单元②: 由单元刚度方程得 M 由单元刚度矩阵得 [4E1:2EI:]M9 “= 要受 1,M 单元③: 由单元刚度方程得 rF8:1 由单元刚度矩阵得 = () 其次,考虑图12-8a所示矩形刚架各结点的变形谐调条件,将单元杆端位移编码换为其相 应的结点位移编码,此时,各单元的刚度方程及刚度矩阵各元素下标也要相应改变
由单元刚度矩阵得: 由单元刚度矩阵得 由单元刚度矩阵得

对于单元①,由式(c)、(d),并根据结构的变形谐调条件议=41,=△,可得 M 2 r26E4]1 = k]1 k”k8」2 对单元②,由式()、(),并根据结构变形谐调条件=42,P=△,可得 6 222 3 始83 对单元③,由式(g)、(h),并根据结构变形谐调条件时=41,=4,可得 「F81 4 (m) ( 如图12-8俄e、f、g得相应的平衡方程 F8+F8=F,+】 M+M=M M=M: (o) 将式().(k)、(m)代人式(o)可得 「k0+k9k8 (p) 上式就是忽略轴向变形的矩形刚架的结构刚度方程
如图 12-8 俄 e、f、g 得相应的平衡方程