
第十二章矩阵位移法 12-1概述 用经典的力法和位移法求解超静定结构,随着基本未知量数目的增多,相应需要建立和 求解的多元代数方程的个数也增多,计算工作极为冗繁和困难。由于计算技术的飞速发展, 电子计算机广泛应用于结构分析,使力学学科在计算技术上实现了现代化,大大推动了工程 设计技术上的改进和结构理论的发展。基于上述情况,结构矩阵分析方法已从本世纪六十年 代迅速发展起来 在结构矩阵分析中,运用矩阵进行计算,不仅能使公式非常紧凑,而且在形式上规格统 一,便于使计算过程程序化,因而适用于电子计算机进行自动化的数学计算。 结构矩阵分析的两种基本方法是矩阵位移法(刚度法)和矩阵力法(柔度法),前者在计算中 采用结点位移作为基本未知量,后者则采用多余力作为基本未知量。对于杆件结构,矩阵位 移法比矩阵力法便于编制通用的程序,因而在工程界应用较为广泛。 矩阵位移法与位移法在本质上 无区别,两者的差异仅在于矩 车位移法是从电算这一角 度出发,它在解题步骤上以矩阵作为组织运算的数学工具。在杆件结构的矩阵位移法中,把 复杂的结构视为有限个单元(杆件)的集合,各单元彼此在结点处连接而组成整体。因而先把 结构分解成有限个单元和结点,即对结构进行离散化。继而对单元进行分析,建立单元杆端 力与杆端位移之间的关系。再根据变形谐调条件、静力平衡条件使离散化的结构恢复为原结 构,从而形成结构刚度方程, 居此不难求解结构的结点位移和单元杆端 力 矩阵位移法的 本思路是 先分后合”,即先将结构离散然后集合,这样一分一合的过程,就把复杂结构的计 算问题转化为简单杆件的分析与综合问题了。因此,它的解题方法可分为两大步骤: ()单元分析。研究单元的力学特性。 (2)整体分析。考虑单元的集合,研究整体方程的组成原理和求解方法。 12一2单元刚度矩阵 一、单元的划分 在杆件结构中,一般是把每个杆件作为一个单元。为了计算方便起见,只采用等截面直 杆这种形式的单元,并且还规定荷载只作用于结点处。根据上述要求,划分单元的结点应该 是结物杆件的转折占 、支承点和截面突变点等,这些结点都是根据结构本身的构造 特征来确定的,故称为构造结 -Tp 图12-1 图12-2 例如图12一1所示结构中a,b,c,d、 e,f等都是构造结点。此外,对于集中力作用处,例 如图12 的点g,为保证结构只承受结点荷载,有时也将它作 结点来处理 这种结 点则称为非构造结点(单元上承受荷载的另一处理方法是将它改用等效的结点荷载来替代,这 将在12一7中进行讨论)。结构的所有结点确定后,则结点间的单元也就被确定。 对于曲杆结构(例如拱),可将它化为许多折线来处理,每一直线段取作一个单元。对于 变截面杆件(直的或曲的)可将它化为许多等截面直线单元来处理,并近似的取每一单元中点
第十二章 矩阵位移法 12-1 概述 用经典的力法和位移法求解超静定结构,随着基本未知量数目的增多,相应需要建立和 求解的多元代数方程的个数也增多 ,计算工作极为冗繁和困难。由于计算技术的飞速发展 , 电子计算机广泛应用于结构分析,使力学学科在计算技术上实现了现代化,大大推动了工程 设计技术上的改进和结构理论的发展。基于上述情况,结构矩阵分析方法已从本世纪六十年 代迅速发展起来。 在结构矩阵分析中,运用矩阵进行计算,不仅能使公式非常紧凑,而且在形式上规格统 一,便于使计算过程程序化,因而适用于电子计算机进行自动化的数学计算。 结构矩阵分析的两种基本方法是矩阵位移法(刚度法)和矩阵力法(柔度法),前者在计算中 采用结点位移作为基本未知量,后者则采用多余力作为基本未知量。对于杆件结构,矩阵位 移法比矩阵力法便于编制通用的程序,因而在工程界应用较为广泛。 矩阵位移法与位移法在本质上并无区别,两者的差异仅在于矩阵位移法是从电算这一角 度出发,它在解题步骤上以矩阵作为组织运算的数学工具。在杆件结构的矩阵位移法中,把 复杂的结构视为有限个单元(杆件)的集合,各单元彼此在结点处连接而组成整体。因而先把 结构分解成有限个单元和结点,即对结构进行离散化。继而对单元进行分析,建立单元杆端 力与杆端位移之间的关系。再根据变形谐调条件、静力平衡条件使离散化的结构恢复为原结 构,从而形成结构刚度方程,据此不难求解结构的结点位移和单元杆端力。矩阵位移法的基 本思路是“先分后合”,即先将结构离散然后集合,这样一分一合的过程,就把复杂结构的计 算问题转化为简单杆件的分析与综合问题了。因此,它的解题方法可分为两大步骤: (1)单元分析。研究单元的力学特性。 (2)整体分析。考虑单元的集合 ,研究整体方程的组成原理和求解方法。 12 一 2 单元刚度矩阵 一、单元的划分 在杆件结构中,一般是把每个杆件作为一个单元。为了计算方便起见,只采用等截面直 杆这种形式的单元,并且还规定荷载只作用于结点处。根据上述要求,划分单元的结点应该 是结构杆件的转折点、汇交点、支承点和截面突变点等,这些结点都是根据结构本身的构造 特征来确定的,故称为构造结点。 例如图 12 一 1 所示结构中 a,b,c,d、 e, f 等都是构造结点。此外,对于集中力作用处,例 如图 12 一 1 的点 g,为保证结构只承受结点荷载,有时也将它作为一个结点来处理,这种结 点则称为非构造结点(单元上承受荷载的另一处理方法是将它改用等效的结点荷载来替代,这 将在 12 一 7 中进行讨论)。结构的所有结点确定后,则结点间的单元也就被确定。 对于曲杆结构(例如拱),可将它化为许多折线来处理,每一直线段取作一个单元。对于 变截面杆件(直的或曲的)可将它化为许多等截面直线单元来处理,并近似的取每一单元中点

处的截面作为该单元的截面。显然,采用这样的处理方法,单元划分得越多,其计算结果将 越接近于真实情况。 二、单元杆端力和杆端位移的表示方法 图12一2示一等截面单元色它的两端分别用)表示。当不考虑其两端的约束情况时,共有 六个杆端位移和六个杆端力。i端的杆端位移为,可和可相应的杆端力为FF和M可 端的杆端位移为可、可和弓,相应的杆端力为、%和网。下面说明杆端位移和杆端力的正 负号规定及其矩阵表示方法 的方向,这个坐标系称为单元的局部坐标系。在局部坐标系中,杆端位移和杆端力的正方向 均规定与坐标轴的正方向一致时为正,转角和弯矩的正方向按照右手螺旋法则规定为逆时针 方向,因为图示弯矩(或转角)是绕2轴旋转的亿轴为垂直于O匠了?平面的轴线),当规定它的力 偶矢量与轴的正方向 致时为正 则其正方向应该是逆时针方向。这种正负符号规定不同 材料力学中的规定,而且也与本书其它各章的规定有所不同,学习时需加注意。 若用下 代表单元④的杆端力列向量,6代表杆端位移列向量,则有: F=[Fi F M:Fi Fa M:] 8=[所可到或买可形护 (12-1) 式中各元素是按照先i端后j端并且依少,远的顺序排列的。 三、单元刚度矩阵 用位移法解题时,必须建立反映杆件物理性质的杆端力和杆端位移之间的关系式一转角 位移方程。在矩阵位移法中,这种关系式将用矩阵的形式来表示。杆件转角位移方程的矩阵 表达式称为单元刚度方程:下“=骨,式中矩阵称为单元⊙对应于局部坐标系的单元刚度 矩阵。本节讲述平面杆件结构中等截面直杆的单元刚度方程及其相应的单元刚度矩阵。 1.自由单元的单元刚度矩阵自由单元是指两端不受约束的杆件。下面分别介绍自由 彬架单元、自由梁式单元和自由刚架单元的单元刚度矩阵。 ()自由桁架单元 桁架单元的特点是它只产生轴向变形和只承受轴向力,图12一3所示为两端不受约束 的析架单元的变形和受力情况。它的两端有两个轴向位移买,可和两个轴向力F。、F。若己 知杆端位移,可,则可求出相应的两个轴向力。由胡克定律,参照图12一3b,c,按叠加原 理可得
处的截面作为该单元的截面。显然,采用这样的处理方法,单元划分得越多,其计算结果将 越接近于真实情况。 二、单元杆端力和杆端位移的表示方法 图 12 一 2 示一等截面单元色它的两端分别用 i,j 表示。当不考虑其两端的约束情况时,共有 六个杆端位移和六个杆端力。i 端的杆端位移为 相应的杆端力为 和 端的杆端位移为 ,相应的杆端力为 和 。下面说明杆端位移和杆端力的正 负号规定及其矩阵表示方法。 对单元 ij 建立直角坐标系 ,如图 12 一 2,其中 x 轴与单元的截面形心轴重合,并 规定由 i 到 J 的方向为正, 轴和 轴为杆件横截面的两个主惯性轴,以右手法则定出 轴和 轴 的方向,这个坐标系称为单元的局部坐标系。在局部坐标系中,杆端位移和杆端力的正方向 均规定与坐标轴的正方向一致时为正,转角和弯矩的正方向按照右手螺旋法则规定为逆时针 方向,因为图示弯矩(或转角)是绕 z 轴旋转的(z 轴为垂直于 平面的轴线),当规定它的力 偶矢量与 轴的正方向一致时为正,则其正方向应该是逆时针方向。这种正负符号规定不同于 材料力学中的规定,而且也与本书其它各章的规定有所不同,学习时需加注意。 若用 代表单元④的杆端力列向量, 代表杆端位移列向量,则有: 式中各元素是按照先 i 端后 j 端并且依 的顺序排列的。 三、单元刚度矩阵 用位移法解题时,必须建立反映杆件物理性质的杆端力和杆端位移之间的关系式— 转角 位移方程。在矩阵位移法中,这种关系式将用矩阵的形式来表示。杆件转角位移方程的矩阵 表达式称为单元刚度方程: ,,式中矩阵 称为单元 对应于局部坐标系的单元刚度 矩阵。本节讲述平面杆件结构中等截面直杆的单元刚度方程及其相应的单元刚度矩阵。 1.自由单元的单元刚度矩阵 自由单元是指两端不受约束的杆件。下面分别介绍 自由 彬架单元、自由梁式单元和 自由刚架单元的单元刚度矩阵。 (1)自由桁架单元 桁架单元的特点是它只产生轴向变形和只承受轴向力,图 12 一 3a 所示为两端不受约束 的桁架单元的变形和受力情况。它的两端有两个轴向位移 和两个轴向力 。 若已 知杆端位移 ,则可求出相应的两个轴向力。由胡克定律,参照图 12 一 3b,c,按叠加原 理可得:

1 图12-3 Fiu-EAui-EAui =-A+A (12-2) 上式可以写成矩阵形式: 肉学9日 F (12-3) 若令 「卧K K' -EA EA FS. (12-40 则式(12一3)可简写成 F=K8 (12-5) 上式即为自由桁架单元®的单元刚度方程,矩阵?称为自由朽架单元®对应于局部坐标系 虹y的单元刚度矩阵。由以上分析可知,在矩阵聚中,第一列的两个元素就是当=1(即1 端沿x轴正方向发生单位位移)时,单元的两个杆端力:第二列元素则为“=1(即J端沿y轴正 方向发生单位位移)时,单元的两个杆端力。为了帮助理解,可在?的上方注明各列元素所对 应的杆端位移,而在其右方注 百杆端位移相对应的杆端力,如式(12 所示 由于单元刚度矩阵的行数等于杆端力的分量数,其列数等于杆端位移的分量数,所以单 元刚度矩阵聚是一个方阵。 (2)自由梁式单元 图12-4a所示为自由梁式单元的变形和受力情况、在单元两端的y轴方向产生位移,和
上式可以写成矩阵形式: 若令 则式(12 一 3)可简写成 上式即为自由桁架单元 的单元刚度方程,矩阵 称为自由朽架单元 对应于局部坐标系 的单元刚度矩阵。由以上分析可知,在矩阵 中,第一列的两个元素就是当 =1(即 i 端沿 x 轴正方向发生单位位移)时,单元的两个杆端力;第二列元素则为 =1(即 J 端沿 y 轴正 方向发生单位位移)时,单元的两个杆端力。为了帮助理解,可在 的上方注明各列元素所对 应的杆端位移,而在其右方注明与杆端位移相对应的杆端力,如式(12 一 4)所示。 由于单元刚度矩阵的行数等于杆端力的分量数,其列数等于杆端位移的分量数,所以单 元刚度矩阵 是一个方阵。 (2)自由梁式单元 图12-4a所示为自由梁式单元的变形和受力情况、在单元两端的y轴方向产生位移 和
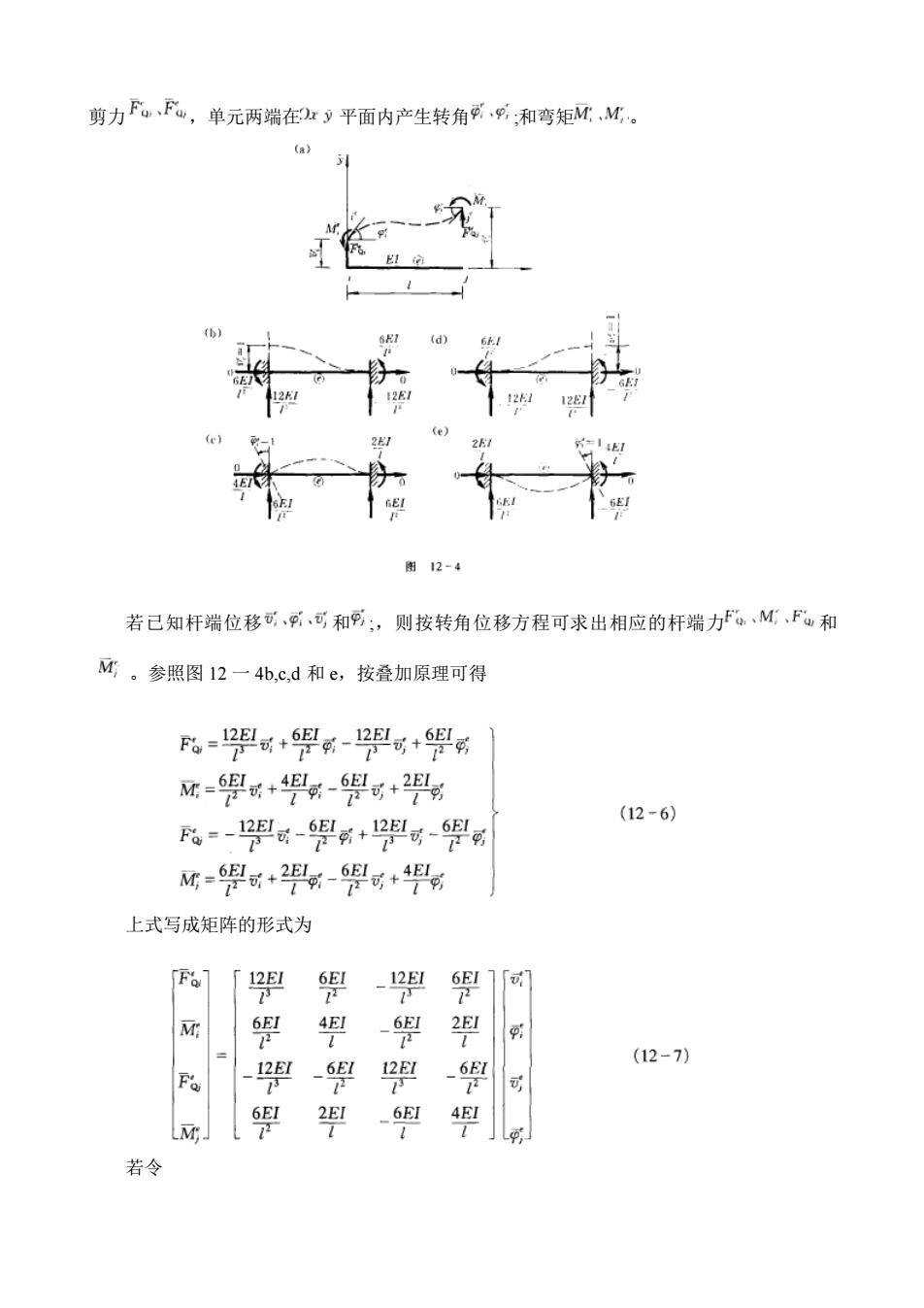
剪力F。,F,单元两端在ry平面内产生转角可,g:和弯矩MM。 图12-4 若已知杆端位移可,可,可和可;,则按转角位移方程可求出相应的杆端力F,M,F和 。参照图12一4b.c,d和e,按叠加原理可得 %-成+职-可+9 -學+-學可+2兴 (12-6) F%=-1票-6县+2-學g M=限可+2-可+ 上式写成矩阵的形式为 [Fo] 「哭 6 1 要 婴 F 哔 (12-7) 可 24 0 为 若令
剪力 ,单元两端在 平面内产生转角 ;和弯矩 。 若已知杆端位移 和 ;,则按转角位移方程可求出相应的杆端力 和 。参照图 12 一 4b,c,d 和 e,按叠加原理可得 上式写成矩阵的形式为 若令

可 可 架 形 7 4 - 要 k'= 型 g 型 (12-8) F g 欧 與 则式(12一7)可简写成 F-k8 (12-9) 上式为自由梁式单元的单元刚度方程,式(12-8)为自由梁式单元的单元刚度矩阵。由 上述分析可知,矩阵聚中第一列的四个元素,就是当“=1(即i端沿x正方向发生单位位 移)时,单元的四个杆端力:其余三列元素的物理意义可依次类推。为了帮助理解,在了 的上方注明各列元素所对应的杆端位移,而在其右方注明与杆端位移相对应的杆端力。 (3)自由刚架单元 图12-2所示为自由刚架单元的变形和受力情况,在单元两端的x轴、y轴方向和:) 平面内,分别产生轴向位移、横向位移和转角,并承受相应的轴向力、剪力和弯矩。 自由刚架单元的刚度方程,可由桁架单元和梁单元的刚度方程进行组合即可得到。 因为目前所研究的是线性变形体系,在弹性小变形范围内,按梁的精确理论分析可知, 杆件的轴向变形与弯曲变形之间的相互影响很小,在一般情况下可以忽略不计,于是将 式(12一3)和式(12一7)进行组合,即可得到自由刚架单元对应于:9局部坐标系的刚度 方程为 F 「坠 -4 0 0 (12-10 0 0 若令
则式(12 一 7)可简写成 上式为自由梁式单元的单元刚度方程,式(12-8)为自由梁式单元的单元刚度矩阵。由 上述分析可知,矩阵 中第一列的四个元素,就是当 =1(即 i 端沿 x 正方向发生单位位 移)时,单元的四个杆端力;其余三列元素的物理意义可依次类推。为了帮助理解,在 的上方注明各列元素所对应的杆端位移,而在其右方注明与杆端位移相对应的杆端力。 (3)自由刚架单元 图12-2所示为自由刚架单元的变形和受力情况。在单元两端的x轴、y轴方向和 平面内,分别产生轴向位移、横向位移和转角,并承受相应的轴向力、剪力和弯矩。 自由刚架单元的刚度方程,可由桁架单元和梁单元的刚度方程进行组合即可得到。 因为目前所研究的是线性变形体系,在弹性小变形范围内,按梁的精确理论分析可知, 杆件的轴向变形与弯曲变形之间的相互影响很小,在一般情况下可以忽略不计,于是将 式(12 一 3)和式(12 一 7)进行组合,即可得到自由刚架单元对应于 局部坐标系的刚度 方程为 若令