
第十一章影响线及其应用 §11-1影响线的概念 大家简单回顾一下,会发现这样的一个现象:在前面各章中,我们所讨论的荷载 均是恒载(大小、方向、在结构上作用位置也就是作用点都不变)。结构在恒载作用 下,反力、内力及变形是一定的。例题中P荷载分别作用于A、B、C、D、E点(4 等分)时引起RA、RB及M图, ↓↓↓↓ 100 但在工程实际中,我们经常会碰到这样的情况: 1)人在独木桥上走,人的重力大小、方向不变,对桥面的作用位置在变,桥墩 两边受力及桥板内力也在变化。(作图) 2)工业厂房中吊车梁承受的吊车荷载。(作图) 3)桥梁上行驶的火车、汽车等荷载。 这些结构所受的荷载有一个共同的特点:荷载的大小、方向未变,但在结构上的 作用位置在移动。 一、移动荷载:(活载的一种) 结构在移动荷载作用下:结构的反力、内力、位移随荷载位置移动而变化,不仅 不同截面的某一量值(反力、M、Q、N或位移等)的变化规律不同:而且同一截面 的不同量值在同样移动荷载作用下的变化规律往往也不相同。如: P-1作用于A处:支座反力及跨中截面的弯矩、剪力 B处: C处: D处: E处: 二、本章主要内容 就是要研究结构上各量值(反力、内力等)随荷载位置移动而变化的规律。(某 指定截面某指定量值》 且体而言,本音主要研究二方面内容 1、如何找出及表示出某量值随荷载移动而变化的规律及变化的范围。 2、求出移动荷载移动到某具体位置时某量值的大小。 3、确定产生某一量值的最大值时移动荷载的位置,也就是说该量值的最不利荷 载位置,进而求出某量值的最大值→作为结构设计的依据。 移动荷载的类型很多,例如:单个集中、多个集中(间距不变)、均布。结构中 某指定处某一量值,受不同的移动荷载作用时,变化规律各不相同,但无须逐个加以 讨论,根据叠加法(弹性范围内,结构中某量值和荷载值成线性比例关系),只要抽 出其中的共性进行分析即可。也就是说:研究竖向单位集中荷载P=1在结构中移动时 对某量值的影响。所以只要找出竖向单位集中荷载在结构上移动时某量值的变化规 44
44 第十一章 影响线及其应用 §11-1 影响线的概念 大家简单回顾一下,会发现这样的一个现象:在前面各章中,我们所讨论的荷载 均是恒载(大小、方向、在结构上作用位置也就是作用点都不变)。结构在恒载作用 下,反力、内力及变形是一定的。例题中 P 荷载分别作用于 A、B、C、D、E 点(4 等分)时引起 RA、RB及 M 图. 但在工程实际中,我们经常会碰到这样的情况: 1)人在独木桥上走,人的重力大小、方向不变,对桥面的作用位置在变,桥墩 两边受力及桥板内力也在变化。(作图) 2)工业厂房中吊车梁承受的吊车荷载。(作图) 3)桥梁上行驶的火车、汽车等荷载。 这些结构所受的荷载有一个共同的特点:荷载的大小、方向未变,但在结构上的 作用位置在移动。 一、移动荷载:(活载的一种) 结构在移动荷载作用下:结构的反力、内力、位移随荷载位置移动而变化,不仅 不同截面的某一量值(反力、M、Q、N 或位移等)的变化规律不同;而且同一截面 的不同量值在同样移动荷载作用下的变化规律往往也不相同。如: P=1 作用于 A 处:支座反力及跨中截面的弯矩、剪力 B 处: C 处: D 处: E 处: 二、本章主要内容 就是要研究结构上各量值(反力、内力等)随荷载位置移动而变化的规律。(某 指定截面某指定量值) 具体而言,本章主要研究三方面内容。 1、如何找出及表示出某量值随荷载移动而变化的规律及变化的范围。 2、求出移动荷载移动到某具体位置时某量值的大小。 3、确定产生某一量值的最大值时移动荷载的位置,也就是说该量值的最不利荷 载位置,进而求出某量值的最大值 → 作为结构设计的依据。 移动荷载的类型很多,例如:单个集中、多个集中(间距不变)、均布。结构中 某指定处某一量值,受不同的移动荷载作用时,变化规律各不相同,但无须逐个加以 讨论,根据叠加法(弹性范围内,结构中某量值和荷载值成线性比例关系),只要抽 出其中的共性进行分析即可。也就是说:研究竖向单位集中荷载 P=1 在结构中移动时 对某量值的影响。所以只要找出竖向单位集中荷载在结构上移动时某量值的变化规

律,便可顺利解决各种移动荷载对该量值的影响。 三、影响线的概念(结合例子说明) 为了研究某指定位置处某一量值随P=1的位置移动而变化的规律,我们引入影响 线的概念。 1、定义:当方向不变的单位集中荷载沿结构移动时,表示结构某一指定处的某一量 值(反力、内力M、Q、N、位移、挠度、转角等)变化规律的图形称为该量值的 影响线。 2、几点说明(定义的内涵) 1)P=1,结构某指定处的某一量值 2)影响线的横坐标x代表:P=1移动的位置:竖标y代表:某确定截面某量值 随之变化情况。 3)影响线与内力图的区别:①荷载不同: ②坐标含义不同:弯矩图X坐标代表:各个截面:Y坐标代表固定荷载作用下 M值分布情况: ③正负号:规定某指定处指定量值的正负号,上正下负,并标上正负号:而弯 矩图画在受拉边。 ④量值的量纲/力的量纲=影响线量纲:反力影响线竖标无量纲,弯矩影响线竖 标为长度量纲,剪力影响线竖标无量纲。 四、作影响线的方法 不能用上面的笨办法;描点法,而有两种方法 1、静力法: 取一坐标系,先设移动荷载P=1处于任意位置x,由静力平衡条件求出所研究的 量值与x之间的函数关系(影响线方程)→作出影响线。 2、机动法: 下面具体讨论不同结构中某指定处某量值的影响线的作法:(如何用静力法作结 构的影响线)。 §11-2用静力法作单跨静定梁的影响线 静力法:将荷载P=1放在任意位置,并选定一坐标系,以横坐标x表示荷载作用点 的位置,然后根据平衡条件求出所求量值与荷载位置x之间的函数关系式.影响线方 程,再根据方程作出影响线图形 一、简支梁的影响线 1、反力影响线 R影响线:∑MB=0R,1-P0-x)=0R影响线:∑M4=0R,l-Px=0 R,=1-/0≤x≤)定两点 Rg=(0≤x≤)定两点 2、弯矩影响线:分段绘出。注:利用已知量值的影响线来作其他量值的影响线 名
45 律,便可顺利解决各种移动荷载对该量值的影响。 三、影响线的概念(结合例子说明) 为了研究某指定位置处某一量值随 P=1 的位置移动而变化的规律,我们引入影响 线的概念。 1、定义:当方向不变的单位集中荷载沿结构移动时,表示结构某一指定处的某一量 值(反力、内力 M、Q、N、位移、挠度、转角等)变化规律的图形称为该量值的 影响线。 2、几点说明(定义的内涵) 1)P=1,结构某指定处的某一量值 2)影响线的横坐标 x 代表:P=1 移动的位置;竖标 y 代表:某确定截面某量值 随之变化情况。 3)影响线与内力图的区别:①荷载不同; ②坐标含义不同:弯矩图 X 坐标代表:各个截面;Y 坐标代表固定荷载作用下 M 值分布情况; ③正负号:规定某指定处指定量值的正负号,上正下负,并标上正负号;而弯 矩图画在受拉边。 ④量值的量纲/力的量纲=影响线量纲:反力影响线竖标无量纲,弯矩影响线竖 标为长度量纲,剪力影响线竖标无量纲。 四、作影响线的方法 不能用上面的笨办法;描点法,而有两种方法 1、静力法: 取一坐标系,先设移动荷载 P=1 处于任意位置 x,由静力平衡条件求出所研究的 量值与 x 之间的函数关系(影响线方程)→ 作出影响线。 2、机动法: 下面具体讨论不同结构中某指定处某量值的影响线的作法:(如何用静力法作结 构的影响线)。 §11-2 用静力法作单跨静定梁的影响线 静力法:将荷载 P=1 放在任意位置,并选定一坐标系,以横坐标 x 表示荷载作用点 的位置,然后根据平衡条件求出所求量值与荷载位置 x 之间的函数关系式.影响线方 程,再根据方程作出影响线图形。 一、简支梁的影响线 1、反力影响线 RA影响线: MB = 0 RA l − P(l − x) = 0 RB影响线: M A = 0 RB l − Px = 0 (0 x l) l R l x A = − 定两点 (0 x l) l R x B = 定两点 2、弯矩影响线:分段绘出。注:利用已知量值的影响线来作其他量值的影响线
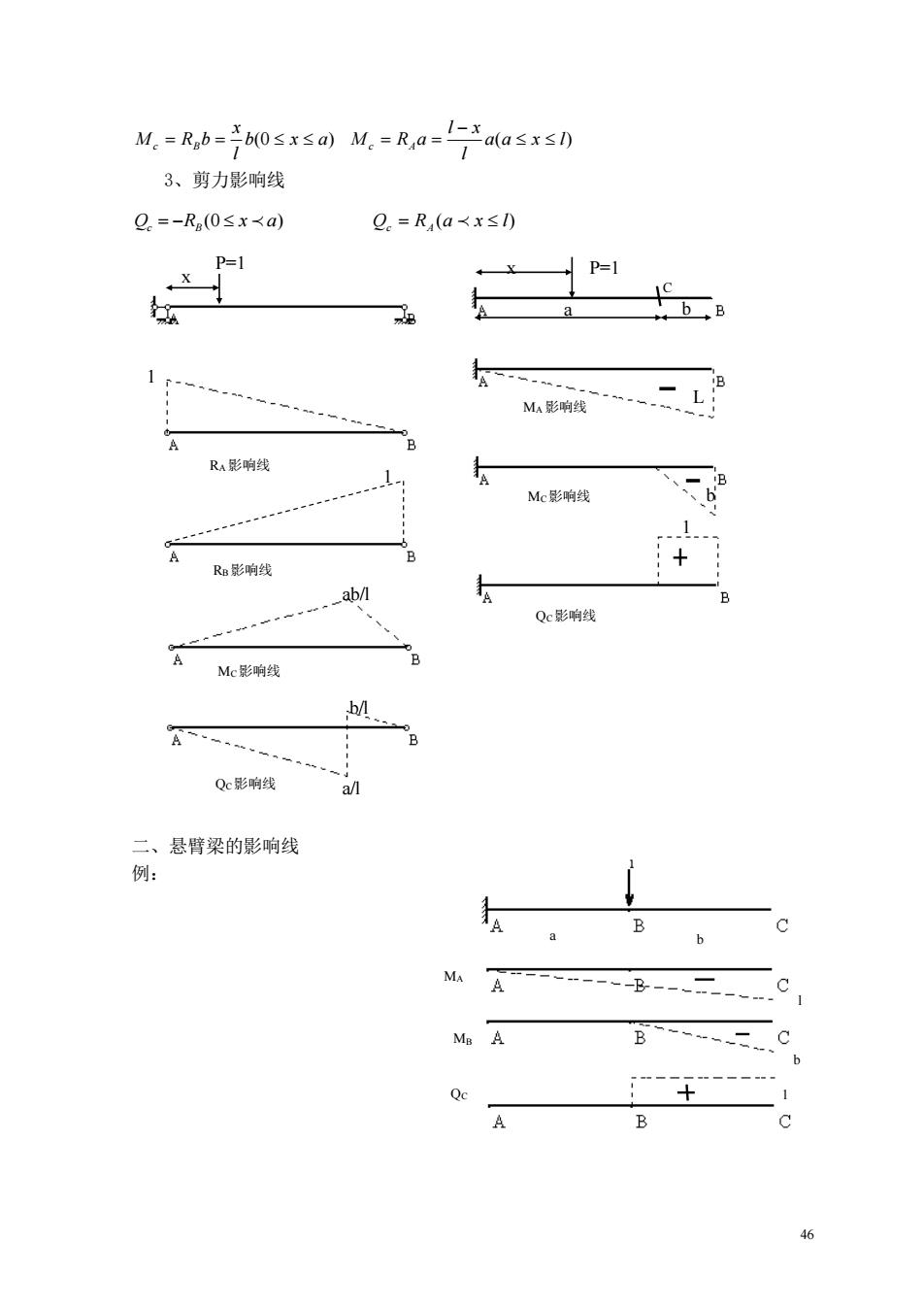
从=860s50M=Ra=产da5xs0 3、剪力影响线 2.=-R(0≤x<a) g.=R,(a<x≤0 P=l RA影响线 Mc影响线 。1。 R影响线 ab/l Qe影响线 Mc影响线 b/l A、 Qc影响线 二、悬臂梁的影响线 例: 46
46 b(0 x a) l x Mc = RBb = a(a x l) l l x M c RAa − = = 3、剪力影响线 Q R (0 x a) c = − B Q R (a x l) c = A 二、悬臂梁的影响线 例: P=1 x 1 1 ab/l a/l b/l RA 影响线 RB影响线 MC影响线 QC影响线 x P=1 C MA 影响线 MC影响线 QC影响线 a b L b 1 MA MB QC a b l b 1

三、外伸梁的影响线(注意和简支梁影响线的关系):P73页图6-5,66 1、反力影响线: R-L-x RB=于(-H≤x≤I+2) 2、跨内部分截面内力影响线 Oc=-Rg Oc=R Mc=Rb(-l≤x<a) Me=R,a(a<x≤I+l2) 3、伸臂部分截面内力影响线 以K点为坐标原点: 0x=-1 Ox=0 M.=-x M=0 D C E D A C B E A C B E C B E C B E OA左影响线 C B E 、 Qx影响线 D A Q右影响线 c E 47
47 三、外伸梁的影响线(注意和简支梁影响线的关系):P73 页图 6-5,6-6 1、反力影响线: l l x RA − = l x RB = ( 2) 1 −l x l + l 2、跨内部分截面内力影响线 QC = −RB QC = RA MC = RBb ( ) −l 1 x a MC = RAa ( ) 2 a x l + l 3、伸臂部分截面内力影响线 以 K 点为坐标原点: QK = −1 QK = 0 M x K = − MK = 0 QA 左影响线 1 QA 右影响线 1 QK 影响线 1

§11-3间接荷载作用下的影响线 一、直接荷载: 间接荷载:房建:主次梁板肋梁楼盖(现浇入、桥梁建筑(铁路桥)画图示意 二、结构受力及传力特点:74页图67 移动荷载加在纵梁上,纵梁(板)是简支梁,两端支承在横梁上,横梁则由主梁支承, 也就是说荷载通过纵梁下的横梁最终传到主梁上(主梁AB受间接荷载(移动荷载)), 同时注意到当P=1在纵梁上任意移动时,主梁只在A、C、E、D、B等有横梁处承受 集中力(主梁上的这些荷载的传递点称为主梁的结点)。主梁承受的是结点荷载。 当P=1在纵梁上移动时,主梁上某处某量值也肯定随之而变化,那么这变化规 律是什么?如何表示出来?也就是主梁在结点(间接)荷载作用下的影响线如何作。 以Mc为例:(分段作)也就是P=I在DE段时,由D、E两结点传给主梁。 个P在D点 ②P在E点 结论一:单位集中荷载加在结点处,结点荷载与直接荷载完全相同,因此在结点荷载 作用下,结构某量值的影响线在结点处的竖标与直接荷载作用下相应的竖标 相等。 当P=I在E、D之间时,离D点x,引起Me的竖标可以用叠加法求得: 此时主梁在D、E处分别受结点荷载作用:~为、 设在直接荷载作用下Mc的影响线在D、E处竖标为:yD.y 则Mc值为: y=二%+于:(DE段内Mc随成直线变化.连接DyE即可) 结论二:在结点荷载作用下任意两相邻结点之间结构的任何量值的影响线均为直线。 三、结点荷载作用下某一量值的影响线作法: 1、先作直接荷载作用下的影响线: 2、取各结点处的竖标,用直线连接相邻两结点的竖标,就得结点荷载作用下的 影响线。 按上面结论可以作出主梁AB的RA、RB、M、QF影响线。 §11-4用机动法作单跨静定梁的影响线
48 §11-3 间接荷载作用下的影响线 一、直接荷载: 间接荷载:房建:主次梁板肋梁楼盖(现浇)、桥梁建筑(铁路桥) 画图示意 二、结构受力及传力特点:P74 页图 6-7 移动荷载加在纵梁上,纵梁(板)是简支梁,两端支承在横梁上,横梁则由主梁支承, 也就是说荷载通过纵梁下的横梁最终传到主梁上(主梁 AB 受间接荷载(移动荷载)), 同时注意到当 P=1 在纵梁上任意移动时,主梁只在 A、C、E、D、B 等有横梁处承受 集中力(主梁上的这些荷载的传递点称为主梁的结点)。主梁承受的是结点荷载。 当 P=1 在纵梁上移动时,主梁上某处某量值也肯定随之而变化,那么这变化规 律是什么?如何表示出来?也就是主梁在结点(间接)荷载作用下的影响线如何作。 以 MC为例:(分段作)也就是 P=1 在 DE 段时,由 D、E 两结点传给主梁。 ① P 在 D 点 ② P 在 E 点 结论一:单位集中荷载加在结点处,结点荷载与直接荷载完全相同,因此在结点荷载 作用下,结构某量值的影响线在结点处的竖标与直接荷载作用下相应的竖标 相等。 当 P=1 在 E、D 之间时,离 D 点 x,引起 MC 的竖标可以用叠加法求得: 此时主梁在 D、E 处分别受结点荷载作用: d d - x 、 d x 设在直接荷载作用下 MC的影响线在 D、E 处竖标为:yD、yE 则 MC值为: D E y d x y d d x y + − = (DE 段内 MC随成直线变化。连接 yD、yE 即可) 结论二:在结点荷载作用下任意两相邻结点之间结构的任何量值的影响线均为直线。 三、结点荷载作用下某一量值的影响线作法: 1、先作直接荷载作用下的影响线; 2、取各结点处的竖标,用直线连接相邻两结点的竖标,就得结点荷载作用下的 影响线。 按上面结论可以作出主梁 AB 的 RA、RB、MF、QF 影响线。 §11-4 用机动法作单跨静定梁的影响线