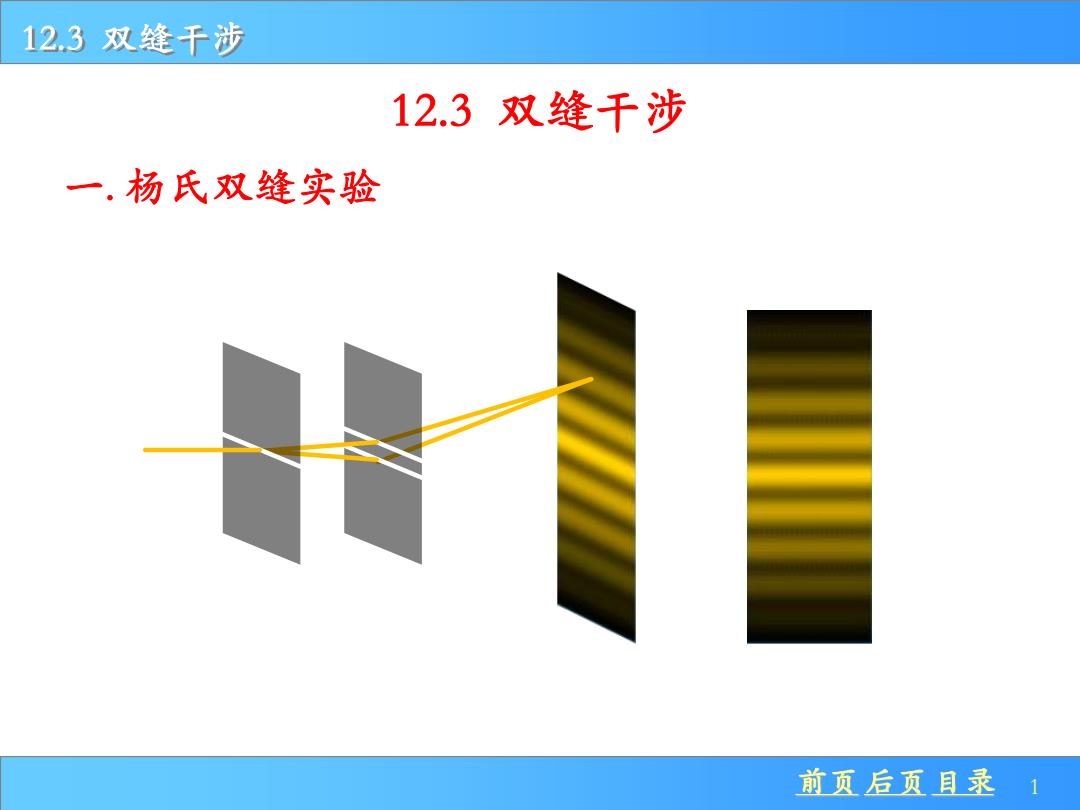
12.3双缝千涉 12.3双缝千涉 一.杨氏双缝实验 前页后页目录 1
前页 后页 目录 1 12.3 双缝干涉 一. 杨氏双缝实验 12.3 双缝干涉
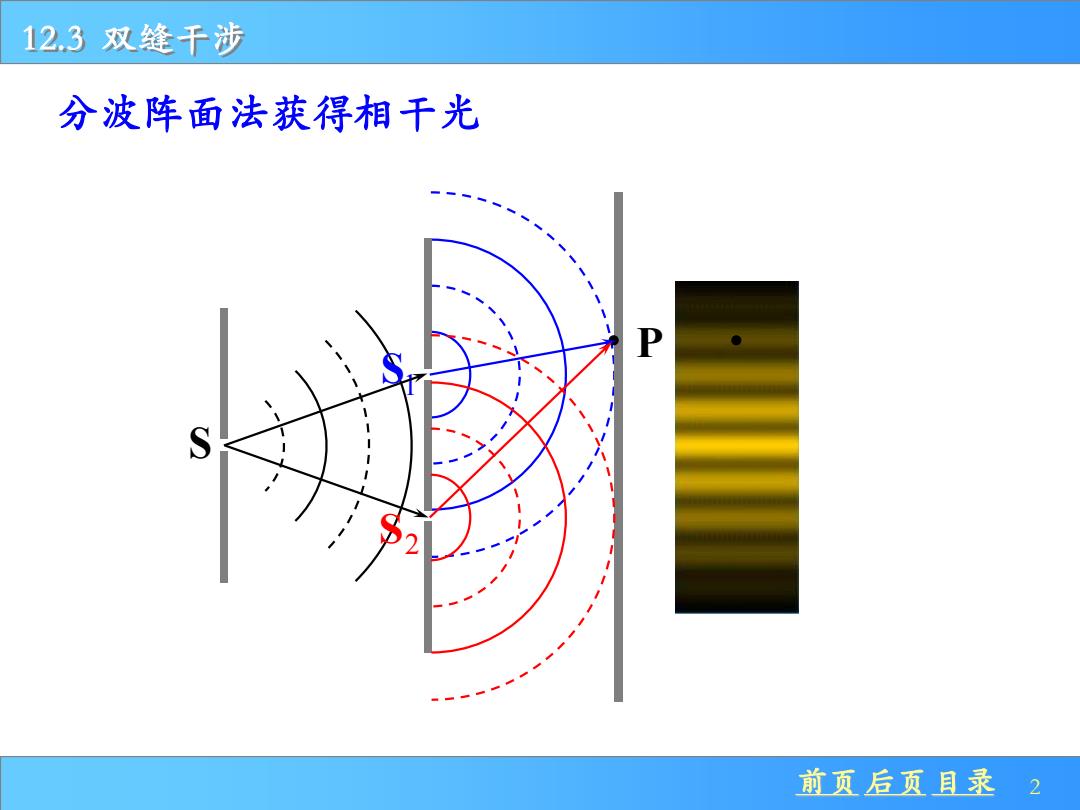
12.3双缝干涉 分波阵面法获得相干光 前页后页目录2
前页 后页 目录 2 12.3 双缝干涉 分波阵面法获得相干光 S S1 S2 P

123双缝千涉 二.干涉明、暗条纹的位置 通常满足 D>>d D>>x sin0≈tan0 波程差 0 6=2-1 ≈d.sing ≈d.tang 相位差△中=2π 6 =d. D 前页后页目录 3
前页 后页 目录 3 12.3 双缝干涉 x d D 1 r 2 r o S1 S2 二.干涉明、暗条纹的位置 通常满足 D d D x sin tan 波程差 2 1 = − r r d sin d tan x d D = P o 相位差 = 2

12.3双缝千涉 1)相长干涉(明纹极大) 6 △p=2π =士2k元 6=±2k (k=0,1,2…) d.x =士2k Xk=+2k D k=0,1,2.…) 2d k称为明纹级 零级明纹(中央明纹) 前页后页目录 4
前页 后页 目录 4 12.3 双缝干涉 1)相长干涉(明纹极大) 2 2 x d k D = 2 0 1 2 2 ( , ) k D x k k , ... d = = k称为明纹级 2 0 1 2 2 k k ( , , ...) = = o x k 0 1 2 3 零级明纹(中央明纹) 2 2k = =

12.3双缝千涉 2)相消干涉(暗纹极小) △=2π=±(2k-1)元 6-2k-月 (k=1,2.…) 0 D x=±2k-l0 (k=1,2…) k称为暗纹级。 前页后页目录5
前页 后页 目录 5 12.3 双缝干涉 2)相消干涉(暗纹极小) 2 1 2 ( ) x d k D = − 2 1 1 2 2 ( ) ( ) k D x k k , ... d = − = 2 1 1 2 2 ( ) ( , ...) k k = − = k称为暗纹级。 o x k 1 2 3 2 2 1 ( ) k = = −