
了匹配情况下束流矩阵与C-S参数间的关系 0 咖pe=V膘·a 0max=√02=√庵 0n-Voz2(1-Ta)-V T210max Xmax =011=VBE CENTROID xt=V61-)=V月 0CpA2010,北京,J1.YTag
匹配情况下束流矩阵与C-S参数间的关系 OCPA 2010, 北京, J. Y. Tang
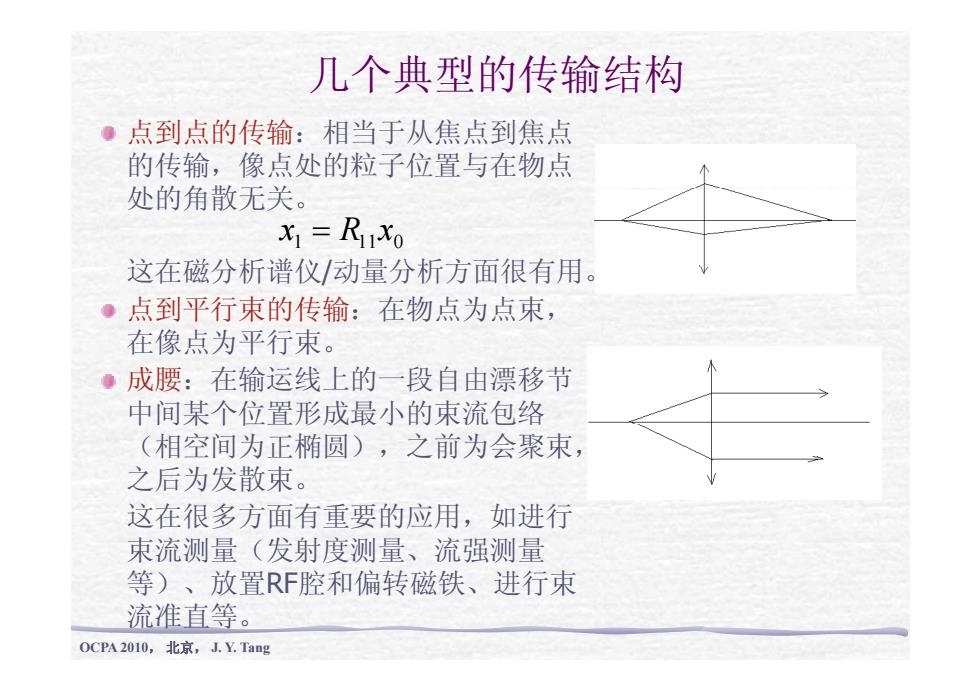
几个典型的传输结构 ●点到点的传输:相当于从焦点到焦点 的传输,像点处的粒子位置与在物点 处的角散无关。 XI=RIXo 这在磁分析谱仪动量分析方面很有用。 ●点到平行束的传输:在物点为点束, 在像点为平行束。 ●成腰:在输运线上的一段自由漂移节 中间某个位置形成最小的束流包络 (相空间为正椭圆),之前为会聚束, 之后为发散束。 这在很多方面有重要的应用,如进行 束流测量(发射度测量、流强测量 等)、放置RF腔和偏转磁铁、进行束 流准直等。 0CpA2010,北京,1.Y.Tang
几个典型的传输结构 点到点的传输:相当于从焦点到焦点 的传输,像点处的粒子位置与在物点 处的角散无关 。 这在磁分析谱仪 /动量分析方面很有用 1 11 0 x = R x 这在磁分析谱仪 /动量分析方面很有用 。 点到平行束的传输:在物点为点束, 在像点为平行束 。 成腰:在输运线上的一段自由漂移节 中间某个位置形成最小的束流包络 (相空间为正椭圆),之前为会聚束, 之后为发散束。 这在很多方面有重要的应用,如进行 束流测量(发射度测量、流强测量 等 ) 放置RF腔和偏转磁铁 进行束 OCPA 2010, 北京, J. Y. Tang 等 ) 、放置RF腔和偏转磁铁 、进行束 流准直等
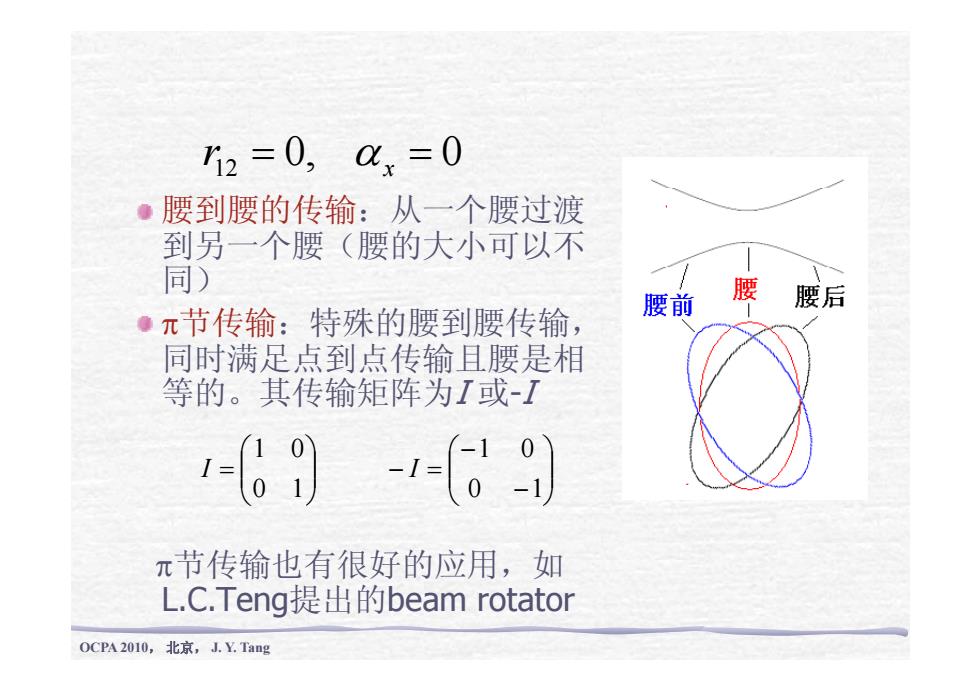
h2=0,ax=0 ●腰到腰的传输:从一个腰过渡 到另一个腰(腰的大小可以不 同) 腰腰后 ·π节传输:特殊的腰到腰传输, 腰前 同时满足点到点传输且腰是相 等的。其传输矩阵为I或-1 π节传输也有很好的应用,如 L.C.Teng提出的beam rotator 0CPA2010,北京,J.YTag
0, 0 r12 = α x = 腰到腰的传输:从一个腰过渡 到另一个腰(腰的大小可以不 同) π节传输:特殊的腰到腰传输, 同时满足点到点传输且腰是相 等的。其传输矩阵为I 或-I ⎟⎟⎠⎞ ⎜⎜⎝⎛ = 0 1 1 0 I ⎟⎟⎠⎞ ⎜⎜⎝⎛ − − − = 0 1 1 0 I π节传输也有很好的应用,如 ⎝ ⎠ ⎝ ⎠ OCPA 2010, 北京, J. Y. Tang L.C.Teng提出的beam rotator

高阶束流传输理论 般情况下,输运线的设计采用线性光学就足够了,但以下几 种情况下需要采取包括高阶效应的分析: ·对束流品质要求比较高(如电镜) 。束流发射度(包括动量分散)很大,线性近似(近轴近似)条件不好, 如在次级束流线上。 。某些利用非线性磁铁进行束流操纵的场合 主要的高阶效应源项 。色差效应:即不同的动量在磁场系统中受到的偏转不同(包括聚焦) ·非线性场效应:磁铁本身是不完美的,除零级场(偏转)和线性场 (聚焦)以外还有更高阶场 。像差效应:非近轴近似以大发射度效应] 理论上可以对束流的二阶和三阶效应进行分析处理,如同线性 矩阵方法一下,也可以采用二阶或三阶传输矩阵(通常称为T 矩阵和U矩阵,与线性的矩阵相对)来表示:更高阶数的理 论分析非常困难。包括二阶以上的相空间分布很复杂,不能用 单纯的相椭圆来代表,最好采用多粒子跟踪进行具体的分析。 0CpA2010,北京,J1.YTag
高阶束流传输理论 一般情况下,输运线的设计采用线性光学就足够了,但以下几 种情况下需要采取包括高阶效应的分析: 对束流品质要求比较高 (如电镜 ) 束流发射度(包括动量分散)很大,线性近似(近轴近似)条件不好, 如在次级束流线上。 某些利用非线性磁铁进行束流操纵的场合 主要的高阶效应源项 色差效应:即不同的动量在磁场系统中受到的偏转不同 即不同的动量在磁场系统中受到的偏转不同 (包括聚焦 ) 非线性场效应:磁铁本身是不完美的,除零级场(偏转)和线性场 (聚焦)以外还有更高阶场 像差效应:非近轴近似 [大发射度效应 ] 理论上可以对束流的二阶和三阶效应进行分析处理,如同线性 矩阵方法一下,也可以采用二阶或三阶传输矩阵 也可以采用二阶或三阶传输矩阵 (通常称为 T 矩阵和 U矩阵,与线性的 R矩阵相对)来表示;更高阶数的理 论分析非常困难 。包括 二阶以上的相空间分布很复杂,不能用 OCPA 2010, 北京, J. Y. Tang 论分析非常困难 。包括 阶以上的相空间分布很复杂,不能用 单纯的相椭圆来代表,最好采用多粒子跟踪进行具体的分析

了包括三阶的传输矩阵 X,④=∑R,X,(0)+∑TaX,(0)X,0)+∑'wX,0)X0)X,0) ●二阶传输矩阵其中一项的传统表示 X0⑩)=RXO)+R2X(O)+R,Y0)+R,Y(O)+R10)+R.0) +T1X2(O)+T12X0)X(O)+T1X0Y0)+T14X0)Y(O)+T1X0)0)+TcXO)60) +T2X(0)X0)+T2X(O)X(0)+T2X(OYO)+T24X(OY(O)+T2X(O10)+T2gX(O)60) +T63(0)+T60)X(0)+T60)Y0)+T60)Y(0)+T601(0)+T6d(O) (实际情况是对一个常规的传输元件,T矩阵中有很多零项) 。在有高阶项的情况下,束流矩阵(σ矩阵)不再代表相椭圆, 其矩阵元代表的是二次矩(second moment)的概念。 0CPA2010,北京,J.YTag
包括 阶的传输矩阵 包括三阶的传输矩阵 X (1) = ∑R X (0) +∑T X (0)X (0) +∑U X (0)X (0)X (0) 二阶传输矩阵其中一项的传统表示 = ∑ +∑ +∑ jkl ijkl j k l jk ijk j k j Xi(1) Rij X j(0) T X (0)X (0) U X (0)X (0)X (0) (0) (0) '(0) (0) (0) (0) '(0) (0) (0) (0) (0) (1) (0) '(0) (0) '(0) (0) (0) 112 113 114 115 116 2 111 11 12 13 14 15 16 δ δ T X T X X T X Y T X Y T X l T X X R X R X R Y R Y R l R + + + + + + = + + + + + (0) (0) '(0) (0) (0) (0) '(0) (0) (0) (0) '(0) (0) '(0) '(0) '(0) (0) '(0) '(0) '(0) (0) '(0) (0) 2 2 121 122 123 124 125 126 δ δ δ δ δ δ δ T T X T Y T Y T l T T X X T X X T X Y T X Y T X l T X + + + + + + + + + + + + + L (实际情况是对一个常规的传输元件,T矩阵中有很多零项) (0) (0) '(0) (0) (0) (0) '(0) (0) (0) (0) 2 162 163 164 165 166 2 +T161δ +T δ X +T δ Y +T δ Y +T δ l +T δ 在有高阶项的情况下,束流矩阵(σ矩阵)不再代表相椭圆, 其矩阵元代表的是二次矩(second moment)的概念。 OCPA 2010, 北京, J. Y. Tang 其矩阵元代表的是二次矩(second moment)的概念