
。C-S不变量 代表单个粒子的振荡能量,通常也是运动中不变的。 Yx2+2axx+Bx=(6)=21 1=(1+2a2)6,ms 了束流光学的描述方法 X 。描迹法:跟踪单个粒子的运动 x' x' ·传输矩阵法:将束流作为一个整体来 考虑 y ●6维相空间: y' =M y 每个粒子除初始条件外是相同的,6N △1 维相空间简并为6维相空间。 p MP 3个投影相平面(xx,y-y°,中-△p/p)。 0CpA2010,北京,J1.YTag
C-S不变量 代表单个粒子的振荡能量,通常也是运动中不变的。 x x x x x x 2 xx x ( ) 2I 2 2 γ + α ′ + β ′ = ε = I (1 2 )2 ⎛ x ⎞ ⎛ x ⎞ rms I (1 2α )ε 2 = + 束流光学的描述方法 y x x y x x ⎟⎟⎟⎞ ⎜⎜⎜⎛ ′ ⎟⎟⎟⎞ ⎜⎜⎜⎛ ′ 描迹法:跟踪单个粒子的运动 传输矩阵法:将束流作为一个整体来 考虑 l y y M l y y ⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜ Δ′ = ⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜ Δ′ 考虑6维相空间: 每个粒子除初始条件外是相同的 6N f i p p l p p l ⎟⎟⎟⎟⎠ ⎜⎜⎜⎜⎝ ΔΔ ⎟⎟⎟⎟⎠ ⎜⎜⎜⎜⎝ Δ 每个粒子除初始条件外是相同的,6N Δ 维相空间简并为6维相空间。 3个投影相平面 (x-x’, y-y’, φ-Δp/p)。 OCPA 2010, 北京, J. Y. Tang 3个投影相平面 (x x , y y , φ Δp/p)。 f i
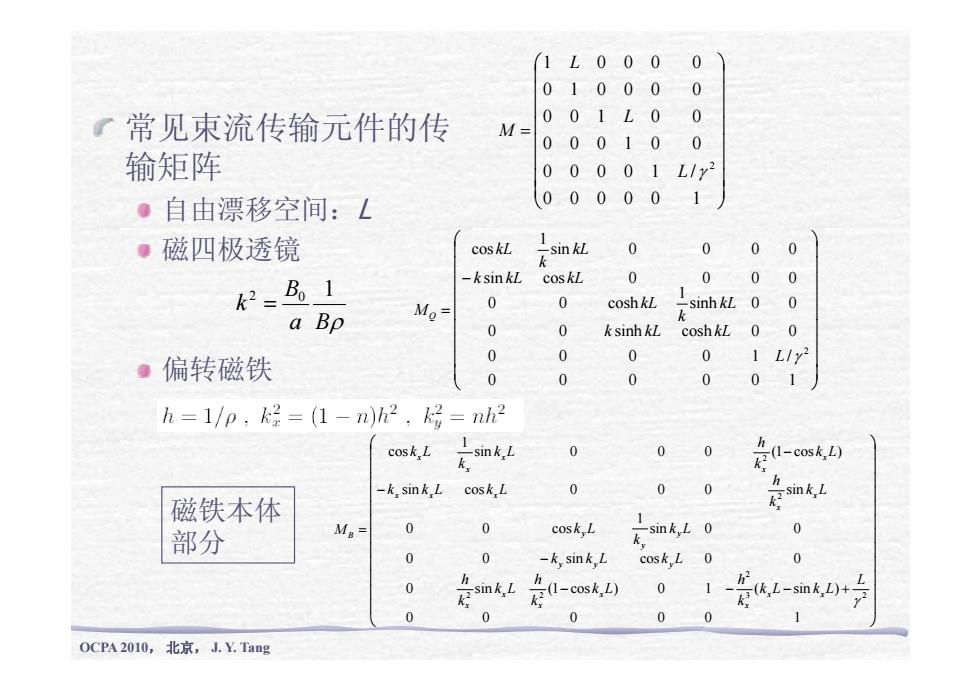
1L000 0 0 01000 常见束流传输元件的传 001L0 0 M= 000100 输矩阵 00001L1/y2 ·自由漂移空间:L 000001 ·磁四极透镜 coskL 咖红 0 0 0 0 =马1 -k sin kL coskL 0 000 1 a Bp Mo= 0 0 coshkL sinh kL 00 0 0 k sinh kL coshkL 00 ·偏转磁铁 0 0 0- 01L1y2 0 0 0 001 h=1/p,k=(1-n)h2,号=nh2 cosk,L 在sn长红 0 0 0 (-cosk,) h -k,sin k L cosk,L 0 00 h 磁铁本体 咖长L Mo= 0 0 coskL mL0 1 0 部分 0 0 -k,sin k,L cosk,L 0 0 0 咖L h (1-cosk,L) 01 2 0 0 0 0 0 0CPA2010,北京,J.YTag
⎟ ⎟ ⎟ ⎞ ⎜ ⎜ ⎜ ⎛ 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 L L 常见束流传输元件的传 输矩阵 ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ = 0 0 0 0 1 / 0 0 0 1 0 0 0 0 1 0 0 2 L γ L M 自由漂移空间: L 磁四极透镜 ⎟ ⎠ ⎜ ⎝ 0 0 0 0 0 1 ⎟ ⎟ ⎞ ⎜ ⎜ ⎛ sin 0 0 0 0 1 cos kL k kL ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ − = 0 0 sinh cosh 0 0 sinh 0 0 1 0 0 cosh sin cos 0 0 0 0 k kL kL kL k kL k kL kL k M Q a Bρ B k 2 0 1 = 偏转磁铁 ⎟ ⎟ ⎟ ⎠ ⎜ ⎜ ⎜ ⎝ 0 0 0 0 0 1 0 0 0 0 1 / 2 L γ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ − − sin cos 0 0 0 sin sin 0 0 0 (1 cos ) 1 cos 2 2 k L k h k k L k L k L k h k L k k L x x x x x x x x x 磁铁本体 ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ − = 0 0 sin cos 0 0 sin 0 0 1 0 0 cos 2 h h h L k k L k L k L k k L k M y y y y y y x B 磁铁本体 部分 OCPA 2010, 北京, J. Y. Tang ⎟ ⎟ ⎟ ⎠ ⎜ ⎜ ⎜ ⎝ − − − + 0 0 0 0 0 1 0 sin (1 cos ) 0 1 ( sin ) 2 2 3 2 γ L k L k L k h k L k h k L k h x x x x x x x
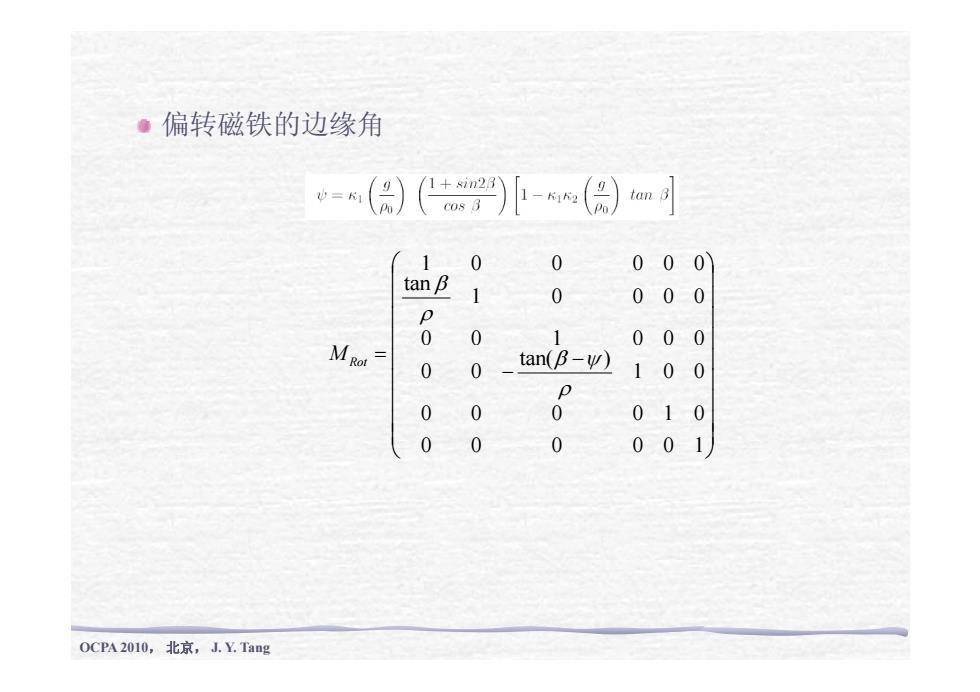
●偏转磁铁的边缘角 心= 1+in2 cos B 1 0 0 000 tanB 1 0 000 p 00 1 000 M Rot= 0 0 tan(B-y) 100 0 0 0 010 00 0 001 0CPA2010,北京,1.YTag
偏转磁铁的边缘角 ⎟⎞ ⎜⎛ 1 0 0 0 0 0 ⎟⎟⎟⎟⎞ ⎜⎜⎜⎜⎛ 0 0 1 0 0 0 1 0 0 0 0 tan1 0 0 0 0 0 ρβ ⎟⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜⎜ − − = 0 0 0 0 1 0 1 0 0 tan( ) 0 0 ρ MRot β ψ ⎟⎟⎠ ⎜⎜⎝ 0 0 0 0 0 1 OCPA 2010, 北京, J. Y. Tang

束流传输的一般表示 装配矩阵 ●一系列传输元件的总作用 R R12 R RIs R16 矩阵(装配矩阵)是单个 R21 R22 R23 RA R25 R26 元件传输矩阵的乘积(有 R= R31 R32 R33 R34 R35R6 时也称为R矩阵): Ra R32 R43 Ri Ras R46 R52 R56 M=Mn…M2M1 束流矩阵的变换 O:=M.O0MI =MooM 0CpA2010,北京,J.YTag
束流传输的一般表示 装配矩阵 一系列传输元件的总作用 ⎟ ⎟ ⎞ ⎜ ⎜ ⎛ 11 12 13 14 15 16 R R R R R R R R R R R R 矩阵(装配矩阵)是单个 元件传输矩阵的乘积(有 时也称为 R矩阵 ) ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ = 31 32 33 34 35 36 21 22 23 24 25 26 R R R R R R R R R R R R R R R R R R R 时也称为 R矩阵 ): M = M n L M 2 M1 ⎟ ⎟ ⎟ ⎟ ⎠ ⎜ ⎜ ⎜ ⎜ ⎝ 51 52 53 54 55 56 41 42 43 44 45 46 R R R R R R R R R R R R R R R R R R 束流矩阵的变换 n 2 1 ⎝ R61 R62 R63 R64 R65 R66 ⎠ T σ x = M x σ x 0 M x T σ = Mσ 0 M OCPA 2010, 北京, J. Y. Tang

了六维束流矩阵的表示 σ矩阵具有关于对角线的对称性 ●r矩阵又称为是关联矩阵(beam matrix correlations) T' a' 011 V011 MM 021 02 V022 MR T21 031 032 033 y V033 MM T31T32 041 042 043044 Vo4 MR T41 T42 T43 T51 052 053054055 V055 MM T61 T52T53T54 061 062063064065 066 V066 PM T61T62 T63T64T65 0i词 ”12<0代表相椭圆是会聚的: 0i0l1顶 lr≤1 r12>0代表相椭圆是发散的 T21=T12= V1+a7 √丙 0CPA2010,北京,1.Y.Tag
六维束流矩阵的表示 σ矩阵具有关于对角线的对称性 r矩阵又称为是关联矩阵(beam matrix correlations) Î r12<0代表相椭圆是会聚的; r12>0代表相椭圆是发散的. OCPA 2010, 北京, J. Y. Tang