应盘读写系统的数学视型 磁盘读写系统的数学模型 曲部(Flexure,一片有弹性的金属)使得读写头浮动于磁盘面上方 100nm的间隙之间。贴片电阻读写头读取磁通量并把信号传递至放大 器。图4中的误差信号读取自事先记录在索引轨道中的误差。 控制装置 输入 执行器和读写臂 误差 电压 +⑧ 放大器 直流电机和摇臂 期望 实际 磁头 传感器 磁头 位置 读写头和磁盘上的索引轨道 位置 图4:磁盘读写系统方框图 1口·1,之4三至分只C 控制系统综合 自动控制原理 电子信息学院6159
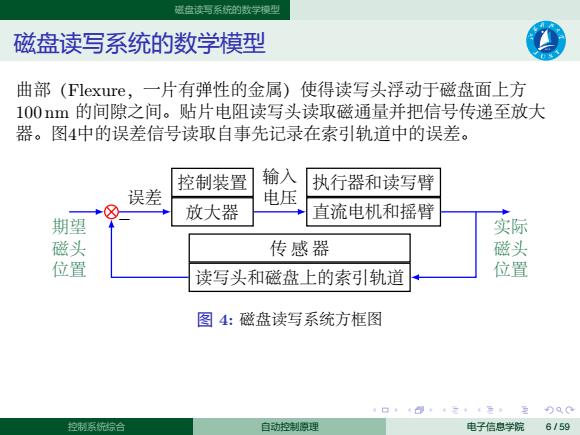
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 磁盘读写系统的数学模型 磁盘读写系统的数学模型 曲部(Flexure,一片有弹性的金属)使得读写头浮动于磁盘面上方 100 nm 的间隙之间。贴片电阻读写头读取磁通量并把信号传递至放大 器。图4中的误差信号读取自事先记录在索引轨道中的误差。 期望 磁头 位置 误差 放大器 控制装置 输入 电压 直流电机和摇臂 执行器和读写臂 实际 磁头 读写头和磁盘上的索引轨道 位置 传 感 器 − 图 4: 磁盘读写系统方框图 控制系统综合 自动控制原理 电子信息学院 6 / 59

盘读写系统的学模型 磁盘读写系统的数学模型 假设读写准确,则传感器的传递函数为Hs)=1,如图5所示。永磁电机 和线性放大器的模型也如图5所示。为了更好的近似,这里使用电枢控制 直流电机的模型。 E(s) 放大器 执行器和读写臂G(s) V(s) Ka R(s) G(8)=sJs+bLs+可 Y(s) 传感器 H(s)=1 图5:磁盘读写系统方框图 图5的模型假定曲部是刚体,也就是不会显著发生形变。以后将会考虑有 形变的模型,不再是完全的刚体。 控制系统综合 自动控制膜理 电子信息学院7159
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 磁盘读写系统的数学模型 磁盘读写系统的数学模型 假设读写准确,则传感器的传递函数为 H(s) = 1,如图5所示。永磁电机 和线性放大器的模型也如图5所示。为了更好的近似,这里使用电枢控制 直流电机的模型。 R(s) E(s) Ka 放大器 V(s) G(s) = Km s(Js+b)(Ls+R) 执行器和读写臂 G(s) Y(s) H(s) = 1 传感器 − 图 5: 磁盘读写系统方框图 图5的模型假定曲部是刚体,也就是不会显著发生形变。以后将会考虑有 形变的模型,不再是完全的刚体。 控制系统综合 自动控制原理 电子信息学院 7 / 59

应营读马系统的数学视型 磁盘读写系统的数学模型 表A-1:磁盘驱动器的典型参数 参数 符号 典型值 读写头和读写臂的转动惯量 J 1Nm s2/rad 阻力 20Nms/rad 放大器 Ka 10-1000 电枢电阻 R 12 电机常数 Km 5N/A 电枢电感 L 1mH 表A-1为磁盘驱动系统的典型参数,于是,我们有: Km 5000 G(s)=s(Js+B)(Ls+R) (A-1) s(s+20)(s+1000) 控制系统综合 自动控制膜理 电子信息学院8159
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 磁盘读写系统的数学模型 磁盘读写系统的数学模型 表 A-1: 磁盘驱动器的典型参数 参数 符号 典型值 读写头和读写臂的转动惯量 J 1 N m s 2/rad 阻力 b 20 N m s/rad 放大器 Ka 10-1000 电枢电阻 R 1Ω 电机常数 Km 5 N /A 电枢电感 L 1 mH 表A-1为磁盘驱动系统的典型参数,于是,我们有: G(s) = Km s(Js + b)(Ls + R) = 5000 s(s + 20)(s + 1000) (A-1) 控制系统综合 自动控制原理 电子信息学院 8 / 59

盘读写系统的数学模型 磁盘读写系统的数学模型 还可以写为: G(s)= Km/(bR) s(TLS+1)(Ts+1) (A-2) 其中TL=J/b=50ms,T=L/R=1ms。由于T≤TL,常常可以忽略 T,于是可以有 G(s)≈ Km/(bR) 0.25 5 s(TLs+1)s(0.05s+1) =s8+20 闭环系统的方框图如下: E(s) Ka G(s) R(s) Y(s) 图6:闭环系统方框图 口4得,4二¥4三至OQG 控制系统综合 自动控制膜理 电子信息学院9159
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 磁盘读写系统的数学模型 磁盘读写系统的数学模型 还可以写为: G(s) = Km/(bR) s(τLs + 1)(τ s + 1) (A-2) 其中 τL = J/b = 50 ms,τ = L/R = 1 ms。由于 τ ≪ τL,常常可以忽略 τ,于是可以有 G(s) ≈ Km/(bR) s(τLs + 1) = 0.25 s(0.05s + 1) = 5 s(s + 20) 闭环系统的方框图如下: R(s) E(s) Ka G(s) Y(s) − 图 6: 闭环系统方框图 控制系统综合 自动控制原理 电子信息学院 9 / 59

磁盘读写振统的数学视型 磁盘读写系统的数学模型 相应的闭环传递函数: Y(s) KG(s) 0.12 R(s)1+KaG(s) (A-3) 使用上面给出的G(s的二阶近似模 0.08 型,得到: 0.04 Y(s) 5Ka R(s) s2+20s+5Ka 0.02 当K。=40,可得 0.10.2030.40.50607 Time (s) 200 图7:图6中系统在R(s)=!时的响应 Ys)=2+20s+200 R(s) 在R()=下的阶跃响应如右图。 日。@,之¥三至)00 控制系统综合 自动控制膜理 电子信息学院10159
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 磁盘读写系统的数学模型 磁盘读写系统的数学模型 相应的闭环传递函数: Y(s) R(s) = KaG(s) 1 + KaG(s) (A-3) 使用上面给出的 G(s) 的二阶近似模 型,得到: Y(s) R(s) = 5Ka s 2 + 20s + 5Ka 当 Ka = 40,可得 Y(s) = 200 s 2 + 20s + 200 R(s) 在 R(s) = 0.1 s 下的阶跃响应如右图。 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0 0.02 0.04 0.06 0.08 0.1 0.12 Time (s) y(t) (rad) 图 7: 图6中系统在 R(s) = 0.1 s 时的响应 控制系统综合 自动控制原理 电子信息学院 10 / 59